
Higher_Mathematics_Part_1
.pdf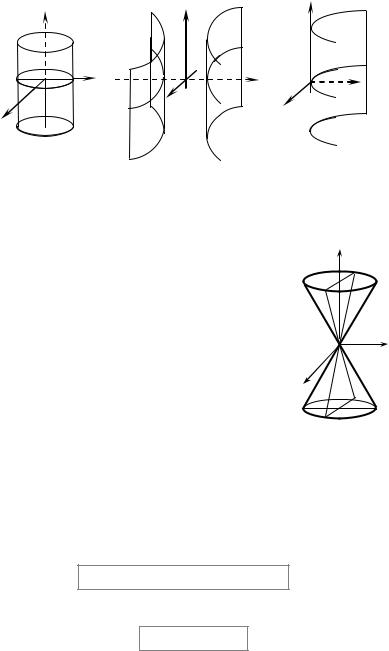
z |
|
|
|
|
|
|
|
|
z |
|
|
|
z |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
О |
|
y |
|
|
|
|
|
О |
|
|
y |
О |
|
|
y |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Fig. 2.27 |
|
|
|
|
|
|
|
Fig. 2.28 |
|
|
|
|
|
Fig. 2.29 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
11.3. Conic surfaces |
|
|
|
|
|
|
|||||||||
The surface is called conic if it is formed by a set of |
|
|
z |
|
|
|
|||||||||||||||||
straight lines (generatrices) passing through the given point |
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||
(vertex) and intersecting the given line L |
(directrix) |
|
|
|
|
|
|
||||||||||||||||
provided the vertex does not belong to the directrix. |
|
|
|
|
|
|
|||||||||||||||||
A standard equation of an elliptic cone looks as |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
x 2 |
|
y 2 |
|
z 2 |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
+ |
|
− |
|
= 0. |
|
(Fig. 2.30) |
|
|
О |
|
|
y |
||||||||
|
|
a 2 |
|
b 2 |
c 2 |
|
|
|
|||||||||||||||
A section of the given cone by the plane |
z = z0 ≠ 0 |
x |
|
|
|
||||||||||||||||||
is an ellipse, by the plane |
|
z = 0 is a point (0; 0; 0) (a |
|
|
|
|
|
|
|||||||||||||||
vertex of the cone).
If a = b = c we have a right circular cone
Fig. 2.30
x2 + y2 = z2 .
11.4. Sphere
A sphere is a surface formed by rotation of a circle around its diameter. An equation of a sphere with a centre at the point M0 (x0 , y0 , z0 ) and a radius R
looks as follows
(x − x0 )2 + ( y − y0 )2 + (z − z0 )2 = R2 .
If the centre of the sphere is the origin we have the following standard equation of the sphere
x2 + y2 + z2 = R2.
131
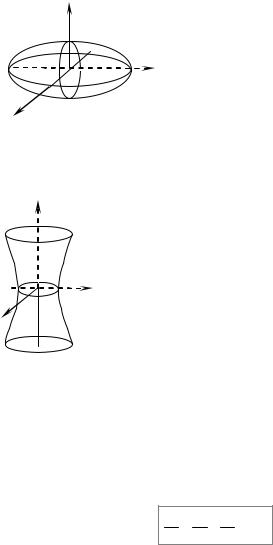
11.5. Ellipsoid
A set of all points in space satisfying the equation
|
|
|
|
|
|
|
|
|
x2 |
+ |
y2 |
+ |
z2 |
|
|
=1. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
a2 |
b2 |
c2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
z |
|
|
|
|
is |
|
called |
|
|
a standard equation of the ellipsoid |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
(Fig. 2.31). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Here the positive numbers а, b, с represent |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
semi-axes of the ellipsoid. |
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
О |
|
|
y |
|
|
|
|
If а = b we have an ellipsod of rotation: |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
x2 |
|
+ |
y2 |
|
+ |
z2 |
|
|
=1 , obtained |
by rotation |
of the |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
a2 |
|
a2 |
c2 |
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
x |
|
|
|
|
ellipse |
|
x |
2 |
+ |
z |
2 |
|
= |
1 about the axis Оz. |
|
||||||||||||||||||||||||||
|
Fig. 2.31 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
a2 |
c2 |
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
11.6. Hyperboloid of one sheet |
|
|
|
|
||||||||||||||||||||||||||||||||
|
z |
A hyperboloid of one sheet (Fig.2.32) is a |
surface |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
described by the equation |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
+ |
y2 |
|
− |
z |
2 |
=1. |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a2 |
b2 |
c |
2 |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
y |
In case а = b we have a rotation hyperboloid of one sheet |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
x |
formed by rotation of the hyperbola |
x2 |
− |
z2 |
=1 , that lies in |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a2 |
|
c2 |
|
||
the plane Охz about the axis Оz.
Fig. 2.32 |
A section of one-sheeted hyperboloid by a plane z = z0 is |
|||
an ellipse, by planes x = x0 |
or y = y0 |
is a hyperbola. |
||
|
||||
We have to note that each point of any one-sheeted hyperboloid is passes by a straight line lying in this hyperboloid entirely.
11.7. Hyperboloid of two sheets
A hyperboloid of two sheets (Fig. 2.33) is a surface described by the equation
x2 + y2 − z2 = −1. a2 b2 c2
132
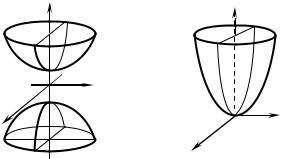
11.8. Elliptic paraboloid
A surface is called an elliptic paraboloid (Fig. 2.34), if its standard equation looks as follows:
|
x2 |
+ |
y2 |
= 2z, ( p, q > 0). |
|
p |
q |
||
|
|
|
||
|
|
|
|
|
If p = q we have a circular paraboloid x2 + y2 = 2 pz formed by rotation of
the parabola x2 = 2 pz lying in the plane Охz about the axis Оz. The point (0; 0; 0) is the vertex of the elliptic paraboloid.
A section of an elliptic paraboloid by the plane |
z = z0 is an ellipse, by the |
||||
planes x = x0 or y = y0 is a parabola. |
|
|
|||
|
z |
z |
|||
|
|
|
|
|
|
|
|
|
|
|
|
Оy
x |
О |
y |
|
||
|
x |
|
Fig. 2.33 |
Fig. 2.34 |
|
11.9. Hyperbolic Paraboloid
A surface is called a hyperbolic paraboloid (Fig. 2.35) if its standard equation is
|
|
|
x2 |
− |
y2 |
= 2z, ( p, q > 0). |
|
|
|
|
p |
q |
|
||
|
|
|
|
|
|
||
|
|
|
|||||
This surface is also called a saddle. |
|||||||
A section of a hyperbolic |
paraboloid by the plane z = z0 ≠ 0 is a |
||||||
hyperbola, by the plane |
z = 0 |
is a pair of two parallel straight lines, by the |
|||||
planes x = x0 or y = y0 |
is a parabola. |
||||||
|
|
|
|
|
|
133 |
|

z
x
y
Fig. 2.35
Micromodule 11
EXAMPLES OF PROBLEMS SOLUTION
Example 1. Determine what surface is defined by the equation:
а) |
|
x2 |
+ |
y2 |
+ |
z2 |
=1 ; |
b) |
x2 − |
z2 |
=1 ; |
в) z2 −4 = 0 ; |
|||||
16 |
|
|
|
|
|||||||||||||
|
9 |
16 |
|
|
|
|
16 |
|
|
|
|
||||||
c) |
4x2 + y2 = 4z ; |
d) |
|
y2 |
+ |
z2 |
− |
x2 |
= 0 . |
||||||||
4 |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
9 |
9 |
|
||||||
Solution. а) The equation
formed by rotation of the ellipse
x2 |
|
+ |
y2 |
|
+ |
z2 |
=1 defines an rotation ellipsoid |
||||
16 |
|
9 |
|
16 |
|
||||||
|
x2 |
|
+ |
y2 |
|
=1 about the axis Оу. |
|||||
16 |
9 |
|
|
|
|
|
|||||
b) The given equation defines a hyperbolic cylinder whose generatrices are parallel to the axis Оу.
c) The equation z2 −4 = 0 is equivalent to the pair of equations z = 2 or z = −2 , whose geometric image is a pair of two parallel planes.
d) We can rewrite the given equation as z = x2 + y2 , but it is an equation of
4
an elliptic paraboloid whose symmetry axis is Оz.
e) The equation |
|
y2 |
+ |
z2 |
− |
x2 |
= 0 describes a circular cone whose symmetry |
|
axis is Ох. |
4 |
9 |
|
9 |
|
|||
|
|
|
|
|
|
|
|
|
Example 2. Transform the equation of a surface 3x2 + 4 y2 − 8z2 − 18x + |
||||||||
+ 8y + 32z − 1 = 0 |
to |
the |
standard form and determine which surface it |
|||||
describes. |
|
|
|
|
|
|
|
|
Solution. We can transform the left member of the equation by completing perfect squares:
134
3x2 +4 y2 −8z2 −18x +8y +32z −1 =
3(x2 −6x +9) +4( y2 +2y +1)−8(z2 −4z +4) −1−27 −4 +32 = = 3(x −3)2 +4( y +1)2 −8(z −2)2 .
So the given equation looks as follows:
3(x −3)2 + 4( y +1)2 −8(z −2)2 = 0 ,
or
|
(x −3)2 |
+ |
( y +1)2 |
− |
(z −2)2 |
= 0. |
|||||
8 |
|
|
6 |
|
|
|
3 |
||||
|
|
|
|
|
|
|
|
||||
After introducing new variables |
x = x −3, |
y = y +1, z = z −2 , we can get |
|||||||||
an equation |
|
|
|
|
|
|
|
|
|
||
|
|
|
x 2 |
+ |
y2 |
− |
z 2 |
|
= 0, |
|
|
|
|
|
8 |
6 |
3 |
|
|
||||
|
|
|
|
|
|
|
|
|
|||
that is a standard equation of a cone whose vertex is a point P(3; –1; 2) (in the system Оxyz).
Micromodule 11
CLASS AND HOME ASSINMENTS
1. Determine what surface is defined by the following equation:
а) |
x2 |
+ |
y2 |
+ |
z2 |
=1 ; |
b) x2 + |
y2 |
+ |
z2 |
|
= −1; |
c) x2 + |
y2 |
− |
z2 |
= −1 ; |
||
|
|
|
|
|
|
|
|
|
|||||||||||
5 |
7 |
25 |
|
4 |
9 |
|
|
|
4 |
9 |
|
||||||||
d) 9z2 +4y2 = 36x ; |
e) x2 + z2 − |
y2 |
|
= 0 ; |
f) x2 + z2 −1 = 0 ; |
||||||||||||||
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
||
g) z2 −y2 = x ; |
|
h) x2 −z2 = 0 ; |
|
|
i) x2 + y2 + z2 = 9 . |
||||||||||||||
2. Determine what surface is defined by the following equation:
a)x2 + y2 + z2 −2x +4y +6z −2 = 0 ;
b)5x2 +4 y2 +3z2 +10x −8y −6z = 0 ;
c)y2 +2x −4y +16 = 0 .
3. Find an intersection point of the straight line |
x |
= |
y |
= |
z +2 |
and the |
||||||
4 |
−3 |
|
||||||||||
|
x2 |
|
y2 |
|
z2 |
|
|
4 |
|
|||
surface |
+ |
− |
=1. |
|
|
|
|
|
|
|||
|
16 |
9 |
4 |
|
|
|
|
|
|
|
||
4. Form an equatin of a sphere whose points А(5; 0; –2) and В(1; 4; 0) are endpoints of its diameter.
135
5. Form an equation of a revolution paraboloid obtained by rotation of the
x2 |
= 12y, |
about the axis Оz. |
parabola |
y = 0 |
|
|
|
|
|
|
Answers |
2. а)a sphere; b)an ellipsoid; c)a parabolic cylinder. 3. (4;–3; 2). 4. (x − 3)2 + + ( y − 2)2 + (z + 1)2 = 9 . 5. x2 + y2 = 12z.
Micromodule 11
SELF-TEST ASSINMENTS
11.1. General equation of a second order surface is given. Determine what surface is defined by that equation and reduce it to standard form.
11.1.1.36x2 + 4 y2 − 8y + 9z2 − 32 = 0.
11.1.2.x2 + 2 y2 − 4x + 4 y − 4z + 6 = 0.
11.1.3.x2 + 16 y2 − 4z2 − 4x + 8z = 0.
11.1.4.3x2 + y2 − 6x + 4 y − 2z + 7 = 0.
11.1.5.x2 + 4 y2 − 4x − 24y − 4z + 40 = 0.
11.1.6.x2 + y2 − z2 − 2x + 4y + 6z − 4 = 0.
11.1.7.x2 + y2 − z2 + 4x + 2 y + 4z + 1 = 0.
11.1.8.x2 + y2 − z2 − 6x − 2y − 2z + 9 = 0.
11.1.9.x2 + y2 − z2 − 4x − 4 y − 4z + 4 = 0.
11.1.10.4x2 + y2 − 2z2 − 8x + 4z + 2 = 0.
11.1.11.12x2 + 3y2 + 4z2 − 24x + 12 y + 8z + 16 = 0.
11.1.12.4x2 + 2 y2 + z2 − 8x − 4 y − 4z + 6 = 0.
11.1.13.4x2 + 9y2 + 36z2 − 36y − 72z + 36 = 0.
11.1.14.3x2 + y2 + 9z2 + 12x − 2 y + 4 = 0.
11.1.15.x2 + 5y2 + 5z2 − 4x − 20z − 1 = 0.
11.1.16.3x2 + 4y2 − 4z2 − 8y + 8z − 12 = 0.
11.1.17.3x2 + 2y2 − 6z2 − 6x + 4y − 1 = 0.
11.1.18.x2 + 3y2 − z2 − 4x + 4z + 1 = 0.
136
11.1.19.4x2 + 9y2 − 36z2 + 8x − 18y − 23 = 0.
11.1.20.2x2 + 5y2 − 10z2 + 8x + 20z − 12 = 0.
11.1.21.4x2 + y2 − 4z2 − 16x − 2 y + 21 = 0.
11.1.22.9x2 + y2 − 9z2 + 18x + 2 y + 19 = 0.
11.1.23.2x2 + y2 − 2z2 − 12x − 4 y + 22 = 0.
11.1.24.4x2 + 4 y2 − z2 + 16x + 8y + 2z + 23 = 0.
11.1.25.4x2 + 2 y2 − z2 − 8y − 2z + 11 = 0.
11.1.26.2x2 − y2 − 4x − 2y − 6z + 1 = 0.
11.1.27.5x2 − 4y2 + 10x + 8y − 20z + 1 = 0.
11.1.28.9x2 − 4 y2 − 16 y − 36z − 52 = 0.
11.1.29.4x2 − y2 + 4y − 4z + 4 = 0.
11.1.30.4x2 − y2 − 16x − 2y − 4z + 7 = 0.
137

Моdule
3
INTRODUCTION TO MATHEMATICAL ANALYSIS. DERIVATIVES AND DIFFERENTIALS OF A FUNCTION OF ONE VARIABLE.
APPLICATIONS OF DERIVATIVES
MODULE STRUCTURE
Micromodule 12. Sequence. The limit of a numerical sequence. Theorems about limits.
Micromodule 13. The Concept of a function. Classification of functions. Limits of function. Theorems about limits.
Micromodule 14. Honorable limits.
Micromodule 15. Comparison of infinitesimals. Equivalent infinitesimals. Their application in calculation of limits.
Micromodule 16. Continuity of a function.
Micromodule 17. The derivative. Geometrical, mechanical and physical interpretation. Differentiability and continuity. The differentiation rules. The derivatives of the elementary functions. The derivatives of composite functions.
Micromodule 18. The derivative of an inverse function. The derivative of an implicit function and parametric function. Logarithmic differentiation.
Micromodule 19. The differential of a function. Geometrical interpretation of a differential. Applications of the differentials. A tangent line and a normal.
Micromodule 20. Higher order derivatives and differentials. Leibniz’s formula.
Micromodule 21. Basic theorems of differentiable functions (Fermat’s, Rail’s, Lagrange’s, Cauchy’s theorems). Taylor’s and Maclaurin’s formula. L’Hospital’s rule.
Micromodule 22. The usage of derivative for function investigation. Function monotony. Extremum. Concavity intervals, inflection points. Asymptotes. Minimum and maximum values of a function. General investigation of a function. General plan of graph construction.
Basic concepts. 1. A sequence. 2. A function. 3. A limit. 4. A continuity. 5. A derivative. 6. A differential. 7. A tangent line. 8. Function increase and decrease. 9. Relative extremum. 10. Concavity intervals. 11. Inflection points. 12. Asymptotes.
Key words: sequence — послідовність, limit — границя, continuity — неперервність, discontinuity — розривність, removable discontinuity — усув-
138
на розривність, infinitesimals — нескінченно малі, infinitely large — нескін-
ченно велика, indeterminate form — невизначений вираз, indeterminacy —
невизначеність, domain of definition — область визначення, a range — множина значень, inverse function — обернена функція, еven function —
парна функція, odd function — непарна функція, periodic function —
періодична функція, honorable limit — важлива границя, derivative — похідна, differential — диференціал, relative extremum — відносний екстре-
мум, asymptote — асимптота, inflection point — точка перегину, convexity —
опуклість, concavity –вгнутість.
Main tasks: 1. Evaluation of limits. 2. Investigation of continuity. 3. Evaluation of the first and higher order derivatives. 4. Evaluation of the derivatives of the implicit functions and the parametric functions. Logarithmic differentiation. 5. Evaluation of the differentials of functions. 6. The usage of derivative. 7. The usage of the differentials. 8. Functions investigation. 9. Graph construction.
THE STUDENT MUST BE READY TO DO
THE FOLLOWING ASSIGNMENTS
1.Concepts, definitions, formulations:
1.Sets. Classification of numerical sets. Operations on sets. The modules of a real number.
2.A sequence.
3.A function. Classification of functions. The elementary functions. An inverse function. A composite function.
4.The Limit of a numerical sequence. The Limit of a function. Infinitesi-
mals.
5.Continuity. Continuity of a function at a point and on an interval. Properties of continuous functions. Points of discontinuity and its classification.
6.Definition of a derivative. Geometrical and physical interpretation.
7.A table of derivatives.
8.Rules of differentiation.
9.A connection between continuity and differentiability.
10.A differential. Geometrical interpretation of a differential.
11.The usage of the differentials.
12.Evaluation of the first and higher order derivatives.
13.Leibniz’s formula.
14.Lagrange’s formula.
15. L’Hospital’s rule for expansion of indeterminate forms 0 |
|
or ∞ |
. |
0 |
|
∞ |
|
16. Taylor’s formula. |
|
|
|
17. Maclaurin’s formula. |
|
|
|
139
18.Investigation for function increase and decrease on the given interval.
19.Investigation of a function for extremum.
20.Minimum and maximum values on the interval.
21.Concavity intervals. Inflection points.
22.Asymptotes.
23.Plan of graph construction.
2.Proofs and conclusions
1.Theorems about limits.
2.The first and the second honorable limits.
3.Theorems about equivalent infinitesimals.
4.The derivatives of elementary functions.
5.The first order and higher order derivatives of the parametric functions.
6.Theorem about continuity of differentiable functions.
7.Geometrical interpretation of the first order differential.
8.Equation of a tangent line and a normal to the curve.
9.Lagrange’s and Fermat’s theorems.
10. L’Hospital’s rule for expanding of indeterminate form |
0 |
. |
|
0 |
|
11.The necessary monotony conditions.
12.The necessary and sufficient extremum conditions.
13.Curve asymptotes seeking rule.
3.Assignments
1.Find the derivatives of functions.
2.Find the derivatives of composite functions, implicit functions and parametric functions.
3.Find the differentials of functions.
4.Find the derivatives and the differentials of higher order.
5.Solve tasks for geometrical and physical interpretation of a derivative.
6.Investigate elementary functions.
7.Sketch the graphs of elementary functions.
8.Evaluate the limits.
9.Evaluate the limits using the equivalent infinitesimals.
10.Investigate functions for continuity.
11.Find different limits with the help of L’Hospital’s rule.
12.Find intervals of function increase and decrease, local extremum.
13.Find concavity intervals.
14.Find graph asymptotes.
15.Construct the graph.
140
