Higher_Mathematics_Part_1

Example 2. Find points of discontinuity of the function

Solution. The given function is determined on all the numerical axis except

It is given by three different formulas for different intervals of changing the argument x and can have discontinuities at points where its analytical expression varies, i.e. at x = 1, x = 2,5. At all other points of the domain of

definition the function f (x) is continuous so as any of three formulas represents

an elementary function, continuous in the interval of changing the argument x. Let us study the behavior of the function at the points x = 1 and x = 2,5 :

191

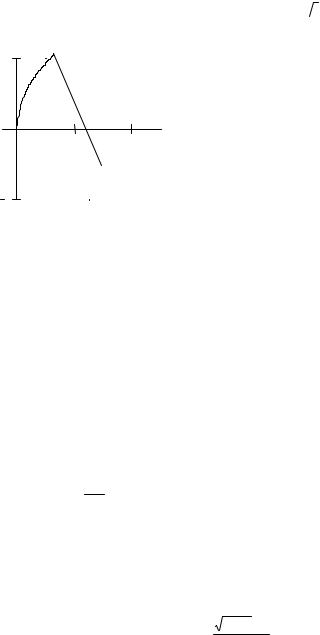
Micromodule 17

BASIC THEORETICAL INFORMATION

DERIVATIVE

The derivative, its geometrical and physical concept. Differentiability and continuity. The rules of differentiation. The derivatives of the elementary functions. The derivative of composite function (The chain rule for differentiation).

Literature: [2, chapter 4], [3, chapter 4, items 4.1—4.2], [4, part 5], [6, chapter 5, §§ 1, 2], [7, chapter 6, § 16], [9, chapter 4, § 2, 4, 5], [10, chapter 4, § 1], [11, chapter 3, §§ 1—15], [8].

17.1. Some problems leading to understanding of the derivative definition

1. The instantaneous velocity of non-uniform motion. Suppose that a body begins to move at the moment of time t = 0 along the straight line. Let the path

traveled by the body over the time t is defined by the formula S = f (t) . A

interval t , the more reasons we may have to consider the motion over the time t and t + t to be uniform.

The limit

if it exists, is called the instantaneous velocity at the instant of time t .

2. The rate of the chemical reaction. Suppose the chemical reaction begins at an instant of time t . Let us designate the quantity of substance, which reacted

till the instant of time t is c(t) . The quantity of substance, which started to react during time interval [t; t + t] , equals c(t + t) − c(t). The ratio

196

c(t + t) − c(t)

y = f (x + x) − f (x)

is called the increment of a function at point x. The increment of argument x ≠ 0 may gain both positive and negative meanings but the meaning x + x

does not go beyond the limits of the domain of the function f (x) .

Definition 3.20. A function, which has the finite derivative at point x , is called differentiable at this point.

Notations for derivative: y′(x), f ′(x) (Lagrange’s notation) or dydx , dfdx

(Leibniz’s notation). From the definition of the derivative it follows that the derivative y' (x) at point x is a number. However, if such a number exists for each inner point of the interval (a, b) , the derivative, then, can be considered as a function of a point x from the given interval.

17.3. The geometrical, physical and mechanical concept of the derivative

Let us try to give the geometrical interpretation of the derivative. We’ll consider the graph of a function y = f (x) at the neighbourhood of point x0 (see

Fig. 3.14). Let P0 be a point of the curve with components (x0 ; f (x0 )) , and P be a point of the graph with components (x0 + x; f (x0 + x)). A straight line, drawn trough the points P0 and P , is called the secant line. If, at the indefinite approach of point P along the graph of a function y = f (x) to point P0 , the secant line P0 P approaches some boundary position ( straight line P0 K ), then this boundary position of the secant line is called the tangent line to the curve y = f (x) at the point P0 .

Let α be the angle, which the tangent line forms with the positive direction

The geometrical concept of the derivative is follows: the derivative of a function y = f (x) at pointі x0 equals the slope of the tangent line to the graph

of a given function at the respective point, that is,

The straight line that passes through the point of contact, perpendicular to the tangent line is called the normal line (it is the straight line P0 N in Fig. 3.14).

The equation of the normal line is

The mechanical concept of the derivative. If S = S(t) is the law of motion of a material point (it means that the dependence of the traversed path S on t is given), the derivative S′(t) , then, is velocity v of a point at moment t ; the second derivative S′′(t) is the instantaneous acceleration a of a point at moment t and the third derivative S ′′′(t) is a jerk of a point at moment t , that is,

v = S′(t), a = S′′(t) = v′(t), j = S′′′(t) = v′′(t) = a′(t).

199

17.4. The main rules of differentiation

Let functions u(x), v(x), w(x) be differentiable at point хand С is a constant. Then