
Higher_Mathematics_Part_1
.pdf
product of normal vectors |
JG |
= { A1, B1, C1} |
and |
JG |
= { A2 , B2 , C2} as a direction |
n1 |
n2 |
||||
vector aG of the straight line. |
|
|
|
|
|
Remark. We can reduce the equation (2.19) to the symmetric form by another way: to find two points Μ1(x1, y1, z1) and Μ2 (x2 , y2 , z2 ) on the straight
line L and to take the vector M1M 2 as a direction vector of the straight line L.
9.5. An angle between two straight lines.
Conditions of parallelism and perpendicularity of two straight lines
Let two straight lines L1 and L2 are given by symmetric equations:
L |
: |
x −x1 |
= |
y −y1 |
= |
z −z1 |
, |
L |
: |
x −x2 |
= |
y −y2 |
= |
z −z2 |
|
|
|
|
|
|
|||||||||
1 |
|
l1 |
|
m1 |
|
n1 |
2 |
|
l2 |
|
m2 |
|
n2 |
|
|
|
|
|
|
|
|
|
|||||||
The angle φ between these lines is equal to the angle between their direction vectors a1 = {l1;m1;n1 } and a2 = {l2 ;m2 ;n2 }, that is,
|
cos ϕ = |
|
a1a2 |
|
|
= |
|
l1l2 |
+ m1m2 + n1n2 |
|
. |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
a1 |
|
|
a2 |
|
|
l2 |
+ m2 |
+ n2 |
l2 |
+ m2 |
+ n2 |
|
||
|
|
|
|
|
|
|
|
|
|
1 |
1 |
1 |
2 |
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
If two straight lines L1 |
|
and |
L2 |
are |
parallel, |
their |
direction vectors are |
||||||||||
parallel too. It means that their corresponding coordinates are proportional. Thus a condition of parallelism of two straight lines is:
|
|
|
|
l1 |
|
= |
m1 |
= |
n1 |
. |
|
|||
|
|
|
|
l |
2 |
m |
n |
|||||||
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|||
If two straight lines |
L |
and L |
|
are perpendicular, their direction vectors are |
||||||||||
|
1 |
2 |
|
|
|
|
|
JG |
|
JJG |
|
|
||
perpendicular too. So their dot product |
a1 |
× a2 |
= 0. Therefore a condition of |
|||||||||||
perpendicularity of two straight lines is:
l1l2 +m1m2 +n1n2 = 0.
9.6. Angle between a straight line and a plane. Conditions of parallelism and perpendicularity of a straight line and a plane
An angle between a straight line and a plane is defined as an angle between a straight line and its projection onto the plane (Fig. 2.14).
Let a straight line L be given by symmetric equations (2.18), and a plane P has a general equation (2.12). We denote an angle between the straight line L
111
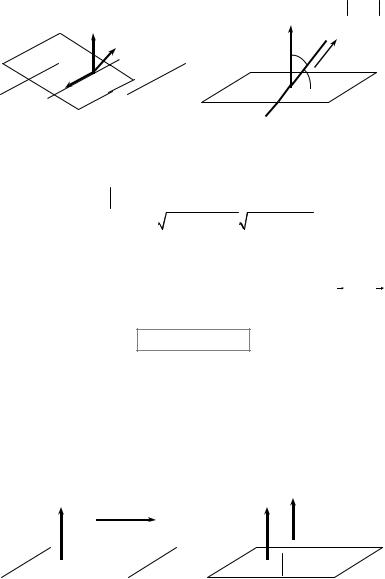
and the plane P by φand an angle between a normal vector of the plane P and a direction vector of the straight line L by ψ. For an acute angle ψφ= 90˚– ψand cos ϕ = sin ψ. For
an obtuse angle ψ φ = ψ – 90˚ and sin ϕ = cos ψ. In both cases sin ϕ = cos ψ .
|
JJG |
|
|
|
|
n |
|
|
|
|
|
n2 |
|
JG |
|
|
|
|
|
||
|
|
|
|
n1 |
|
|
|
G |
G |
|
|
|
|
|
|
|
|
ψ |
a = n1 |
× n2 |
|
|
G |
G |
G |
|
|
|
|
|||
|
|
φ |
|
|
|
|||||
|
a |
= n1 |
× n2 |
|
|
|
|
|
||
|
|
|
|
|
|
|||||
|
Fig. 2.13 |
|
|
Fig. 2.14 |
|
|
|
|||
So, the angle between a straight line and a plane may be found by the
formula: |
|
|
G |
|
G |
|
|
|
|
|
|
|
|
sin ϕ = |
|
n × a |
|
|
= |
|
Al + Bm + Cn |
|
. |
||
|
JJG |
|
G |
|
|
|
|
|
||||
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
||||||
|
|
n |
× |
a |
|
A2 + B2 + C2 l2 + m2 + n2 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
9.7. Condition of parallelism of a straight line and a plane
If a straight line is parallel to a plane (Fig. 2.15) vectors n and a are perpendicular, so their scalar product is equal to zero:
Αl + Βm +Cn = 0.
9.8. Condition of perpendicularity of a straight line and a plane
If a straight line is perpendicular to a plane (Fig. 2.16), vectors n and aG are collinear, thus their coordinates are proportional:
|
|
|
|
|
|
Α |
= |
Β |
= C . |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
l m |
n |
|
|
|
||||
|
nG |
|
aG |
|
n |
|
a |
|||||||
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
Fig. 2.15 |
|
|
Fig. 2.16 |
|||||||||
112

9.9. Intersection point of a straight line and a plane
To find an intersection point of the straight line given by the equations (Fig.2.16) and a plane, it is necessary to solve the system of equations
|
|
|
x |
− x0 |
|
y − y0 |
|
z − z0 |
|
|
||||
|
|
|
|
|
|
|
= |
|
|
= |
|
|
|
|
|
|
|
|
l |
|
m |
|
|
n |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||||
or |
|
|
Ax + By + Cz + D = 0 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x = x0 + lt, |
|
|
|
|
|
|
|
|
|
|
||||
y = y |
+ mt, |
|
|
|
|
|
|
|
|
|
||||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
z = z0 |
+ nt, |
|
) |
|
0 |
|
|
0 |
|
0 |
|
|||
|
( |
Al + Bm + Cn |
|
+ By |
+ Cz |
+ D = 0. |
||||||||
|
|
t + Ax |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A number of solutions of the latter system is determined by the equation
Rt + S = 0, where R = Al + Bm + Cn, S = Ax0 + By0 + Cz0 + D. Next cases are possible:
1) if R≠0, then the equation Rt + S = 0 has the only root t* = − RS . So the
straight line and the plane have one common point ( x0 +lt*, y0 +mt*, z0 +nt * );
2) if R = 0, S ≠ 0 then the equation Rt + S = 0 has no solution. It means, that the straight line and the plane have no common points;
3) if R = 0, S = 0, the equation Rt + S = 0 has an infinite set of solutions. In this case the straight line lies on the plane.
So, if a straight line lies in a plane, two conditions are valid:
Al + Bm + Cn = 0,
Ax0 + By0 + Cz0 + D = 0.
The first equation means parallelism of a straight line and a plane, and the second means that the point Μ0 (x0 ; y0 ; z0 ) of straight line L lies in the plane.
9.10. Distance between parallel straight lines
A distance between parallel straight lines
L : |
x − x1 |
= |
y − y1 |
|
= |
z − z1 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|||||||||
1 |
|
l |
m |
|
|
|
n |
|
|
|
|||||||
|
|
|
|
|
|
|
|
||||||||||
and L2 : |
|
x − x2 |
= |
y − y2 |
= |
z − z2 |
, |
|
|
M2 |
|||||||
|
|
|
|
|
|
|
|||||||||||
|
|
|
l |
m |
|
|
|
n |
|
|
|||||||
equals a height of a parallelogram built on the |
L2 |
|
d |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
vectors a and M1M 2 , where |
M1 is an arbit- |
|
M1 |
||||||||||||||
|
a |
||||||||||||||||
rary point of the line |
L1 , |
and M2 is an |
L1 |
||||||||||||||
arbitrary point of the line L2 (Fig. 2.17). |
|
|
Fig. 2.17 |
||||||||||||||
113
|
|
|
|
aG |
|
|
|
|
|
Thus, |
d = |
|
M1M2 |
|
. |
||||
|
|
|
|
|
|
|
|||
|
|
|
|
aG |
|
|
|||
|
|
|
|
|
|
|
|
|
|
The distance between parallel straight lines may be found by the next scheme:
1)to draw a plane through the point M1 (x1 ; y1; z1 ) , perpendicular to the straight line L1 ;
2)to find an intersection point О of the plane with the straight line L2 ;
3)to calculate the length of a line segment M1O. The result will be the required distance between parallel straight lines.
Micromodule 9
EXAMPLES OF PROBLEMS SOLUTION
Example1. Find symmetric equations of a straight line
2x − 5y + 2z − 10 = 0,
x − 2y − z + 1 = 0.
Solution. To write down symmetric equations of a straight line you must just know coordinates of its point and direction vector.
Let us take such a point that its ordinate y = 0 , the other coordinates must satisfy the left equations:
|
|
|
|
2x + 2z − 10 = 0, |
or |
x + z = 5, |
||||||||||||||
|
|
|
|
|
− z + 4 = 0, |
|
|
|
|
|||||||||||
|
|
|
|
x |
|
|
|
|
|
|
x − z = −1, |
|||||||||
|
Its solution is x = 2, |
z = 3. |
So a point |
Μ(2; 0; 3) belongs to the given |
||||||||||||||||
straight line. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
We can find a direction vector by the formula: |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
G |
G |
G |
i |
|
j |
|
k |
|
|
|
|
|
|
|
|
||
|
|
|
2 −5 2 |
= 9i + 4 j + k , |
||||||||||||||||
|
|
|
a |
= n |
× n = |
|||||||||||||||
|
|
|
|
1 |
2 |
1 |
−2 |
−1 |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
or |
aG = |
{ |
9; 4;1 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
} |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
So symmetric equations of the straight line are:
x − 2 |
= |
y |
= |
z − 3 |
. |
9 |
4 |
|
|||
|
1 |
|
|||
114
Example 2. Prove that straight lines |
|
|
|
||||||
|
x − 3 |
= |
y − 1 |
= |
z + 2 |
and |
2x + 3y − 8z + 5 = 0, |
||
|
|
|
|
|
|
− 5z + 1 = 0 |
|||
1 |
− 2 |
3 |
|
||||||
|
|
|
|
3x + y |
|||||
are perpendicular.
Solution. Straight lines are perpendicular if and only if direction vectors of
these straight lines are perpendicular. A vector |
1 |
|
{ |
} |
is a direction |
aJG |
= |
|
1; − 2; 3 |
vector of the first straight line. A direction vector of the second straight line may be found by the formula:
|
|
|
i |
G |
G |
|
|
|
|
|
|
|
|
|
aG |
= nG × nG = |
j |
k |
= −7iG− 14 Gj − 7kG = −7(iG+ 2 Gj + kG). |
||||||||||
2 3 −8 |
||||||||||||||
2 |
1 |
2 |
3 |
1 |
−5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Let us calculate a dot product |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
a1a2 = 1 1− 2 2 + 3 1 = 0. |
|
|
|
||||||||
So the straight lines are perpendicular. |
|
|
|
|
|
|
|
|||||||
Remark. Similar |
straight |
lines are |
perpendicular |
if a |
triple product |
|||||||||
a1n1n2 = 0. |
|
|
|
|
|
|
|
|
y − 1 |
|
|
|
|
|
Example 3. Prove that the straight line |
x + 1 |
= |
= |
z − 2 |
|
lies in the plane |
||||||||
2 |
4 |
−1 |
||||||||||||
4x − 3y − 4z + 15 = 0. |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
Proof. The first way. It is enough to show that any two points of the straight line lie in the plane.
Actually, points Μ1 (−1; 1; 2) and Μ2 (1; 5; 1) lie on the straight line
(explain the choice of these points). Having substituted coordinates of these points in the equation of the plane, we get two identities.
The second way. We can represent equations of the straight line in the parametric form:
x = −1+2t, y =1+4t, z = 2−t,
then we can substitute x, y, z in the equation of the plane:
4(−1+ 2t) − 3(1+ 4t) − 4(2 − t) + 15 = 0,
and receive the identity: 0=0. It means that any point of the straight line lies in the plane.
Example 4. Find a point P symmetric to a point M (−2; 3;−5) relative to
the straight line L: |
x − 8 |
= |
y + 1 |
= |
z + 1 |
. |
|
3 |
1 |
|
|
||||
|
|
|
|
−1 |
|||
115
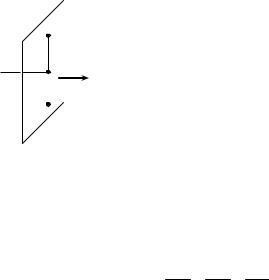
Solution. Let P be a required point (Fig. 2.18). The problem may be solved in such a sequence.
|
|
|
1) We make an equation of the plane α passing |
|
|
|
|
|
|
|
through the point М and perpendicular to the straight |
αМ |
|
|
line L. |
|
|
2) We find a point Q, that is, a projection of the |
|
Q |
|
l |
point M onto the straight line L. |
|
|
|
3) We determine coordinates of the point P, taking |
|
|
a |
into account that the point Q is a midpoint of the line |
|
|
segment MP. |
|
|
|
|
PP |
The vector a = |
{ |
} |
is a direction vector of |
|
3; 1; − 1 |
|||
|
the straight line L and a normal vector of a plane |
|||
Fig. 2.18 |
perpendicular to the straight line L. We write down the |
|||
equations of a plane α as following: |
||||
3(x +2) +( y −3)−(z +5) = 0 or 3x + y − z − 2 = 0.
The point Q belongs both to the plane and to the straight line. To find its coordinates we have to solve the system of equations
x − 8
33x +
=y + 1 = z + 1
1−1 y − z − 2 = 0.
It is convenient to solve such a system by introducing a parameter t we shall write down the equations of a straight line in a parametric form: x=3t + 8, y = t– 1, z = –t–1. Having substituted them in the equation of the plane we shall receive:
3 (3 t + 8 ) + (t – 1) – (– t – 1) – 2 = 0, 11 t + 22 = 0, t = –2.
So, xQ = 3(–2) + 8=2, yQ = –2–1= –3, zQ = 2–1=1.
The point Q(2; −3; 1) is a midpoint of the line segment MP, therefore its coordinates satisfy the equalities
x = |
xM + xP |
, |
y = |
yM + yP |
, |
z = |
zM + zP |
. |
||||
|
|
|
|
|||||||||
Q |
2 |
|
|
Q |
2 |
|
|
Q |
2 |
|
||
|
|
|
|
|
|
|
|
|
||||
That is |
|
|
|
|
|
|
|
|
|
|
|
|
2 = |
−2 + xP |
|
, −3 = |
3 + yP |
, |
|
1 = |
−5 + zP . |
||||
2 |
2 |
|
||||||||||
|
|
|
|
|
|
|
|
2 |
|
|||
From here we find coordinates of the point P(6; ─9; 7).
116
Micromodule 9
CLASS AND HOME ASSIGNMENTS
1. Three vertices of a parallelogram M1 (6; 2; −10) , M2 (9; −5; 6) ,
M3 (2; −8; 4) are given. Find the equations of its diagonals.
2.Write down equations of a straight line in the symmetric form:
|
|
|
x − 2y + 3z + 15 = 0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
− 4z − 12 = 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
2x + 3y |
|
|
|
y + 3 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
3. Find an intersection point of the straight line |
|
|
x − 2 |
= |
= |
z − 1 |
and the |
|||||||||||||||||||||||
3 |
|
|
|
|
−1 |
|||||||||||||||||||||||||
plane x + 2 y − 3z − 9 = 0. |
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
4. Determine an acute angle between straight lines |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
x = 11t − 1, y = −8t + 4, z = −7t + 5 and |
x + 2 |
= |
|
y − 3 |
= |
z − 1 |
. |
|
|
|
|
|
|
|||||||||||||||||
|
|
2 |
−8 |
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
5. Calculate an angle between the straight line |
|
x − 3 |
= |
y − 5 |
|
= |
z + 2 |
|
and the |
|||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||
plane 6x −9 y −6z +10 = 0 . |
|
|
|
|
|
2 |
|
|
|
|
|
−3 |
|
|
−2 |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
6. Find a projection of the point А(1; 2; 8) onto the straight line |
x − 1 |
= |
|
y |
= |
z |
. |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
2 |
|
|
−1 |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
||||||
7. Calculate distance of the point |
P(2; 3; −1) |
to the straight line |
x = t +1, |
|||||||||||||||||||||||||||
y = t +2, z = 4t +13. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
8. Making sure that straight lines |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
x + 7 |
= |
y − 5 |
= |
z − 9 |
and 2x + 2y − z − 10 = 0 |
|
|
|
|
|
|
|
|||||||||||||||||
3 |
−1 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
4 |
|
x − y − z − 22 = 0 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
are parallel, calculate a distance between them.
|
|
|
|
|
|
|
|
|
|
Answers |
|
|
|
|
|
|
|
|
||||
1. |
|
x − 6 |
= |
|
y − 2 |
= |
z + 10 |
, |
x − 1 |
= |
|
y − 2 |
= |
z + 7 |
. 2. |
x + 3 |
= |
y − 6 |
= |
z |
. 3. (5; |
|
2 |
5 |
|
5 |
|
|
|
−1 |
10 |
|
|||||||||||||
|
|
|
−7 |
|
|
−2 |
9 |
|
|
7 |
|
|||||||||||
2; 0). |
4. 60˚. |
5. 90˚. 6. (3; -1; 1). 7. 6. |
8. 25. |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
Micromodule 9 |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
SELF─TEST ASSIGNMENTS |
|
|
|
|
|
||||||||||
9.1. Coordinates of three points M1 , M2 , M3 |
are given(see problem 8.1). Find: |
|||||||||||||||||||||
а) symmetric equations of the straight line passing through the points M1 and M2;
117
b) parametric equations of the straight line passing through the points M1 and M3 ;
c) an angle between straight lines M1M2 and M2 M3 . |
|
|
|||
9.2. Find symmetric equations of a straight line |
|
|
|||
9.2.1. |
x − 4y + 4z − 10 = 0 |
9.2.2. |
x − 2 y + 3z − 6 = 0 |
||
|
|
|
|
||
|
2x + y − 2z − 6 = 0 |
|
2x + 3 − z |
− 8 |
= 0 |
9.2.3. x + 4y + z + 10 = 0
2x − y − 2z + 5 = 0
x − 6y + 3z − 12 = 0
9.2.5.
3x + 2y − 3z − 6 = 0
9.2.7.x + 3y + 2z + 6 = 0
2x + 2y − 3z − 6 = 0
9.2.9.x − 3y + 3z − 7 = 02x + y − z − 3 = 0
9.2.11.3x − 2 y + z − 8 = 0
2x + y − z − 7 = 0
|
3x + y + 4z − 6 = 0 |
|
9.2.13. |
|
|
|
|
|
|
4x − y − 2z |
− 3 = 0 |
9.2.15. |
x − 5y + 3z − 11 = 0 |
|
|
|
|
|
2x + 3y − z |
− 3 = 0 |
9.2.17. |
x − 7 y + 2z − 14 = 0 |
|
|
|
|
|
2x + 4y − z |
− 6 = 0 |
|
|
|
9.2.19. |
3x − 4y + 2z − 15 = 0 |
|
|
|
|
|
x + 2y − 2z |
− 10 = 0 |
9.2.21. |
x + 3y + 3z − 9 = 0 |
|
|
|
|
|
4x + 2y − z |
− 7 = 0 |
9.2.23. |
x − 2y + 4z + 10 = 0 |
|
|
|
|
|
5x + y − 3z |
− 16 = 0 |
118
x + 5y + 2z − 20 = 0
4x + 2y − z − 8 = 0
9.2.6. x − 2y + 3z + 5 = 0
5x + y − 4z − 12 = 0
x − 6y + 2z − 14 = 0
9.2.8.
4x − y − 2z − 8 = 0
2x − 3y + 4z − 15 = 0
9.2.10.
2x + y − 3z − 4 = 0
9.2.12.x − 2y + z − 10 = 0
2x + 3y − 2z − 12 = 0
9.2.14.2x − 3y + 2z − 5 = 02x + 2y − 3z − 4 = 0
9.2.16. x + 6y + 2z − 2 = 0
3x + y − 3z = 0
x − 4y − 4z + 10 = 0
9.2.18.
2x − y + 2z + 6 = 0
5x − y + 2z − 20 = 0
9.2.20.
2x + 2y − z − 4 = 0
9.2.22.x − 8y + 2z + 6 = 02x + y − z + 4 = 0
9.2.24.x − 2y + 4z − 2 = 0
3x + 2y − z − 36 = 0

9.2.25. x − y + z − 5 = 0
3x − 2y − 2z − 4 = 0
x + 3y + 2z − 13 = 0
9.2.27.
2x + y + z − 16 = 0
x − 3y + 6z − 11 = 0
x + 2y − 2z − 5 = 0
x − 2y + 4z − 12 = 0
2x + y − 2z − 6 = 0
9.2.28.3x − y + 2z − 6 = 02x + y − 4z − 8 = 0
9.2.30.x − 4 y + 5z = 0
2x − y − 3z − 2 = 0
9.3.Find: а) an intersection point of a straight line and a plane;
b)an angle between the straight line and the plane;
c)a point symmetric to the point Р relative to the given plane.
9.3.1. |
x −2 |
= |
|
y −3 |
= |
|
z +1 |
, |
x +2 y +3z −14 = 0 , |
P(1; |
3; −6) . |
|||
−1 |
−1 |
|
|
|||||||||||
|
|
|
4 |
|
|
|
|
|
||||||
9.3.2. |
x +1 |
= |
y −3 |
|
= |
z +1 |
|
, |
x +2 y −5z +20 = 0 , |
P(2; |
7; −4) . |
|||
3 |
|
|
|
|||||||||||
|
|
|
|
−4 |
5 |
|
|
|
|
|
||||
9.3.3.x−−11 = y +4 5 = z −2 1 , x −3y +7z −24 = 0 , P(0; 10; −2) .
9.3.4. |
|
x −1 |
= |
|
|
y |
= |
|
z +3 |
, 2x − y + 4z = 0 , P(−4; |
6; 6) . |
|
|
|||||||||||||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
0 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
9.3.5. |
|
x −5 |
= |
|
y −3 |
= |
|
|
z −2 |
, |
3x + y −5z −12 = 0 , |
P(7; 2; −5) . |
||||||||||||||||||||||||||
1 |
|
|
|
|
−1 |
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|||||||||||||||
9.3.6. |
x +1 |
= |
y +2 |
|
|
= |
z −3 |
|
, |
|
|
x +3y −5z +9 = 0 , P(5; 0; −6) . |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
−3 |
|
|
2 |
|
|
|
|
|
|
|
|
|
−2 |
|
|
|
|
|
|
|
|
|||||||||||||||
9.3.7. |
|
|
x −1 |
= |
y −2 |
|
|
|
= |
|
z +1 |
|
, |
x −2y +5z +17 = 0 , P(−12; |
4; |
6) . |
||||||||||||||||||||||
|
|
−2 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
−1 |
|
|
|
|
|
|
|
|
|||||||||||
9.3.8. |
|
|
x −1 |
= |
y −2 |
|
|
|
= |
|
z +−4 |
, x −2y +4z −19 = 0 , P(9; |
0; |
−3) . |
||||||||||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
0 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
||||||||||||||||||
9.3.9. |
|
|
x +2 |
= |
y −1 |
|
= |
z +4 |
, |
2x −y +3z +23 = 0 , P(6; −3; |
2) . |
|||||||||||||||||||||||||||
|
|
−1 |
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
−1 |
|
|
|
|
|
|
|
|
|||||||||||
9.3.10. |
|
|
x +2 |
|
= |
y −2 |
= |
z +3 |
, |
2x −3y −5z −7 = 0 , P(15; |
6; |
0) . |
||||||||||||||||||||||||||
1 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
0 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
9.3.11. |
|
|
x −1 |
= |
y −1 |
|
|
= |
z +2 |
|
, |
4x −2y −z −11 = 0 , |
P(7; 1; |
−1) . |
||||||||||||||||||||||||
|
2 |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
−1 |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
||||||||||||||
119
9.3.12. |
|
x −1 |
= |
|
|
|
|
y +1 |
|
|
|
|
= |
|
|
|
z −1 |
, |
|
|
|
3x −2y −4z −8 = 0 , |
P(−4; |
0; |
8) . |
|||||||||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−1 |
|
|
|
|
|
|
|
||||||||||||||||||||
9.3.13. |
|
x +2 |
|
= |
|
|
|
|
|
y −1 |
= |
|
|
|
|
|
|
|
z +3 |
|
, |
x + 2y − z − 2 = 0 , P(5; |
2; |
−2) . |
||||||||||||||||||||||
|
−1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
1 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
9.3.14. |
|
x +3 |
|
= |
|
|
|
|
y −2 |
|
|
|
|
= |
|
|
|
z +2 |
, |
5x −y +4z +3 = 0 , |
P(9; 5; −3) . |
|||||||||||||||||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
−5 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
9.3.15. |
x −2 |
= |
|
y −2 |
|
|
|
= |
|
|
z −4 |
|
|
|
|
, |
x +3y +5z −42 = 0 , |
P(−2; −4; −6) . |
||||||||||||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
−1 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
9.3.16. |
|
x −3 |
|
= |
|
|
|
y −4 |
|
|
|
|
= |
|
|
z −4 |
, |
7x + y +4z −47 = 0 , P(5; −2; 1) . |
||||||||||||||||||||||||||||
|
−1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
5 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
9.3.17. |
|
x +3 |
|
|
|
= |
y −1 |
|
|
= |
|
|
z −1 |
, |
2x +3y +7z −52 = 0 , P(0; |
6; |
−8) . |
|||||||||||||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
3 |
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
9.3.18. |
|
x −3 |
|
= |
|
|
y +1 |
|
|
= |
z +3 |
|
, |
3x +4 y +7z −16 = 0 , P(−5; 1; −3) . |
||||||||||||||||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
3 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
9.3.19. |
|
x −5 |
|
|
= |
y −2 |
|
= |
|
z +4 |
|
, |
2x −5y + 4z + 24 = 0 , P(2; 2; −4) . |
|||||||||||||||||||||||||||||||||
|
−2 |
|
|
|
|
|
|
|
|
−1 |
|
|||||||||||||||||||||||||||||||||||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
9.3.20. |
|
x −1 |
= |
|
y −8 |
|
|
= |
z +5 |
|
|
, |
x −2 y −3z +18 = 0 , |
P(11; |
4; −3) . |
|||||||||||||||||||||||||||||||
|
8 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
−5 |
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
9.3.21. |
|
x −3 |
|
= |
|
y −1 |
|
|
= |
z +5 |
|
|
, |
x −7 y +3z +11= 0 , |
P(14; 12; −2) . |
|||||||||||||||||||||||||||||||
1 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
−1 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
9.3.22. |
|
x −5 |
|
|
= |
y +3 |
|
= |
|
z −1 |
|
|
, |
3x +7 y −5z −11 = 0 , P(0; 13; −16) . |
||||||||||||||||||||||||||||||||
|
−1 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
5 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
9.3.23. |
|
x −1 |
= |
|
y −2 |
|
|
= |
z −6 |
|
, |
4x + y −6z −5 = 0 , |
P(−1; 11; |
5) . |
||||||||||||||||||||||||||||||||
|
7 |
|
|
|
|
|
|
|
−1 |
|
||||||||||||||||||||||||||||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
9.3.24. |
|
x −3 |
|
= |
|
y +2 |
|
|
= |
z −8 |
, |
5x +9y +4z −25 = 0 , P(7; 0; −4) . |
||||||||||||||||||||||||||||||||||
1 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
−1 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
9.3.25. |
|
x +1 |
|
= |
y |
= |
z +1 |
, x +4 y +13z −23 = 0 , P(−6; 4; −2) . |
||||||||||||||||||||||||||||||||||||||
|
−2 |
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
0 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
9.3.26. |
|
x −1 |
= |
y −3 |
|
= |
z +5 |
|
, |
3x −2y +5z −3 = 0 , |
P(11; |
0; |
−1) . |
|||||||||||||||||||||||||||||||||
|
6 |
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
1 |
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
120
