Файловый архив студентов. Файловый архив студентов.
1261 вуз, 4605 предмет.
/ Регистрация
FAQ Обратная связь Вопросы и предложения
Добавил:
Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Национальный авиационный университет
Предмет:
[НЕСОРТИРОВАННОЕ]
Файл:

Higher_Mathematics_Part_1

.pdf
Скачиваний:
1052
Добавлен:
19.02.2016
Размер:
6.63 Mб
Скачать
☆

 

 

3x + 1

x+3

 

 

 

 

 

 

14.2.29. а)

2

 

;

 

b)

lim logcos3x cos 2x .

lim

 

 

 

 

 

x→∞

3x − 1

3

 

 

 

 

x→0

 

 

 

 

 

 

 

 

 

ln (5x −19)

 

14.2.30. а)

lim

3x + 7

)

x2 −4

;

b)

lim

.

 

 

 

 

 

x→−2 (

 

 

 

 

 

 

x→4 x2 − 5x + 4

Micromodule 15

BASIC THEORETICAL INFORMATION. COMPARISON OF INFINITESIMALS. EQUIVALENT INFINITESIMALS. THEIR APPLICATION IN CALCULATION OF LIMITS

Literature: [3, chapter 3, §§3.1—3.8], [4, section 4, §§4.2—4.3], [6, chapter 4, § 4], [11, chapter 2, § 11], [12].

15.1. Comparison of infinitesimals. Equivalent infinitesimals

Definition 3.14. If the ratio of two infinitesimals α and β has a finite limit

(if x → x0 ) which is different from zero:

lim

α

= q ≠ 0 , then α and β are

 

x→ x

β

 

said to be infinitesimals of the same order if

0

 

 

x → x0 .

We denote it as α(x) = O(β(x)) if x → x0 .

 

 

Definition 3.15. Two infinitesimals α and

β

are said to be equivalent if

lim

α = 1. Then we write down: α ~ β .

 

 

 

x→ x

β

 

 

 

0

 

 

 

 

Definition 3.16. If the ratio of two infinitesimals has a limit equal to the

number 0: lim

α

= 0 i.e. lim

β

 

= ∞ the infinitesimal α is said to be one of

β

α

x→ x

x→ x

 

0

 

0

 

 

 

higher order than

β , and the infinitesimal β is said to be one of lower order

than α.

 

 

 

 

 

We denote it as α(x) = o(β(x))

if x → x0 .

Definition 3.17. An infinitesimal α is said to be an infinitesimal of the k-th order relative to an infinitesimal β if α and βk are the infinitesimals of the

same order(if x → x0 ), i.e. lim

α

= А ≠ 0.

k

x→ x0

β

 

181
Theorem 3.8

For example, 1− cos x is the infinitesimal of the second order relative to

x

 

1− cos x =

 

2sin

2 x

 

= 1 lim

sin

2 x

 

= 1

 

 

 

 

because lim

lim

 

2

 

 

2

 

, x3

and

x

are

x2

 

 

2

 

x→0

x2

x→0

 

2 x→0 x

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

infinitesimals of the third and 0.5 orders relative to x correspondingly.

The remark. The comparison of infinitely large magnitudes is performed similarly to comparison of infinitesimals. Slight difference exists in terms so, if

lim uv = 0 i.e. lim uv = ∞, where magnitudes u and v are infinitely large

magnitudes we say that u is of lower order than v, and v is of higher order than u .

In practical of calculation of limits two theorems about equivalent infinitesimals and infinitely large magnitudes are widely applied.

The limit of a ratio of two infinitesimals will not change by substitution of these infinitesimals by their equivalents.

The similar statement is true for infinitely large magnitudes.

Theorem 3.9 The sum of infinitesimals of different orders is equivalent to its term of the lowest order.

The sum of infinitely large magnitudes of different orders is equivalent to its term of the highest order.

The most important equivalences which follow from formulas (3.2) and (3.3) are:

x sin x tg x arcsin x arctg x ex − 1 ln (1+ x),

(3.5)

1− cos x

1 x2

, ax − 1 x ln a, (1+ x)k

− 1 kx.

 

 

2

 

 

 

Micromodule 15

EXAMPLES OF PROBLEMS SOLUTION

Example 1. Evaluate

lim

lncos 4x+e5x3

− 1−2x 4

 

 

.

 

x→0 arctg 2 3x−73 sin 8 x

Solution. We have an indeterminacy

0

 

0

.

 

 

 

 

 

Using Theorems 3.8 and 3.9, and equivalences (3.5) we get:

lncos 4x = ln(1+ cos 4x − 1) = ln(1 − 2sin 2 2x) ~ − 2 sin 2 2x ~ − 8x2 ,

182

 

 

e5x3 −1 ~ 5x3 ; arctg2 3x

 

~ 9x2 ,

 

 

 

 

 

 

 

 

 

8

 

 

 

 

 

 

 

 

 

 

3 sin8 x

 

~ x

3

,

 

 

 

 

 

 

ln cos 4x + e5x3 − 1− 2x4

 

 

 

−8x2 + 5x3 − 2x4

 

−8x2

 

8

 

 

 

i.e.

lim

 

 

 

 

 

 

 

=

lim

 

 

 

 

 

 

= lim

 

 

 

 

 

 

 

= −

9

.

 

 

 

x→0 arctg2 3x − 73 sin8 x

 

 

 

 

x→0

 

 

8

 

 

 

 

x→0

9x

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

9x2 − 7x3

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Example 2. Evaluate

lim

4 3n3 − 4n2 + 3 5n2 − 8n3

.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

n→∞

 

 

9n2 + 7n − 5 n4 + 6n3

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Solution. We have an indeterminacy ∞

.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

∞

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Let us open it by means of Theorems 3.8 and 3.9.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

4

 

 

 

 

 

 

3

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

As 4 3n3 − 4n2 ~ 4 3n4 ;

3 5n2 − 8n3 ~ − 2n; 9n2 + 7n ~ 3n; 5 n4 + 6n3 ~ n

5

,

then

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

4

3n3

− 4n 2 + 3

5n

2 − 8n3

 

4 3n

4 − 2n

 

 

2

 

 

 

 

 

 

 

 

 

 

lim

 

 

 

 

 

 

 

 

 

 

= lim

 

 

 

 

 

 

 

= −

 

 

 

.

 

 

 

 

 

 

 

 

2

 

 

5

 

4

 

 

 

 

4

 

 

3

 

 

 

 

 

 

 

n→∞

9n

+

7n −

n

+ 6n

3

n→∞

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3n − n 5

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Example 3. Compare infinitesimals α(x) = x2 + 3x + 2 and β(x) = tg(x + 1)

if x → −1.

Solution. Let us evaluate limit of quotient of the given functions:

 

x2 + 5x + 4

 

0

 

x2 + 5x + 4

=

lim

 

=

 

 

= lim

 

x→−1

tg(x + 1)

 

0

 

x→−1

x + 1

 

 

 

= lim

(x + 1)(x + 4)

= lim (x + 4) = 3 ,

 

 

 

 

 

 

 

x + 1

 

 

 

 

 

 

 

x→−1

 

 

 

x→−1

 

 

 

 

 

 

 

that is, the functions α(x)

і β(x)

 

if x → −1 are infinitesimals of the same order.

Example 4. Compare infinitesimals α(x) = x arctg x−2

and β(x) = (x − 3)−1/ 3

if x → ∞ .

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Solution. Let us evaluate limit of quotient of the given functions:

 

 

 

 

 

x arctg x−2

 

= |х–3~х| = lim

x arctg x−2

 

 

 

 

lim

 

 

 

 

 

 

 

 

 

 

 

=

 

 

 

 

 

 

 

 

 

 

 

 

x−1/ 3

 

 

 

 

 

x→∞ (x − 3)−1/ 3

 

 

 

 

 

 

x→∞

 

 

 

 

 

 

arctg x−2

 

x

−2

= t

 

 

arctg t

 

 

t

= lim t

1/ 3

 

 

 

 

 

 

 

 

 

 

= lim

 

 

 

=

 

 

 

= lim

 

 

 

= lim

 

 

= 0

,

x−4 / 3

 

 

 

 

 

 

 

 

 

x→∞

 

 

 

 

 

 

 

 

 

t→0 t2 / 3

 

 

t→0 t2 / 3

t→0

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

that is, α(x) = O(β(x)) if

x → ∞ .

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

183

Micromodule 15

CLASS AND HOME ASSIGNMENT

Evaluate limits using equivalents.

1. lim

ln cos x + ex − cos x − x2

.

 

2.

lim

ln(10 − x2 )

.

 

 

 

arcsin2x+arctg2 3x − x4

 

sin 2π x

 

 

 

x→0

 

 

 

 

 

x→3

 

 

 

3.

lim

 

cos x (e3x − 1)

.

 

 

 

 

4.

lim

x

2 − 4x + 1 − 1

.

 

x→0

 

 

4 1+ x − 1

 

 

 

 

 

 

 

x→0

 

tg π x

 

 

 

Compare infinitesimals.

 

 

 

 

 

 

 

 

 

 

 

 

5.

α(x) = x2 + 6x + 8

and β(x) = tg(x + 2)

if

x → −2 .

 

 

 

6.

α(x) =

arcsin2 (x − 3)

and β(x) = x

3

− 7x − 6

if x → 3.

 

x + 1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

7.

α(x) = x4 − 5x2 + 4 and

β(x) = x2 − 8x + 7

if

x → 1 .

 

8.

α(x) = 3 − 3 x + 20

and

β(x) = 3 2x + 13 − 3 if x → 7 .

 

9.

α(x) = x2 − 1 and

β(x) = 2 ln x

if

x → 1 .

 

 

 

 

 

10. α(x) = 3tg x − 3− tg x ; β(x) = sin2

x

 

if

x → 0 .

 

 

 

Answers

1.–0,5. 2. −π3 . 3. 12. 4. −π2 . 5. α(x) = О(β(x)) . 6. α(x) = о(β(x)) .

7.α(x) ~ β(x) . 8. α(x) = О(β(x)) . 9. α(x) ~ β(x) . 10. β(x) =о( α(x) ).

Micromodule 15

SELF–TEST ASSIGNMENTS

15.1. Evaluate limits using equivalents.

15.1.1. a) lim

 

 

1− cosπ x

 

;

b)

lim

(1+ 2x)5

− 1

.

 

 

 

x→0 ln(1− x) tg π x

 

 

 

x→0

e3x − 1

 

 

 

15.1.2. a) lim

tg3

2x − sin x4

 

;

b)

lim

 

x + ln(1+ x )

.

 

 

x3

 

 

sin

x

 

 

 

x→0

 

 

 

 

 

x→0

 

 

 

15.1.3. a)

lim

 

ln(1+ sin 3 x )

;

b)

 

 

2x3 − 2x

+ 3x

 

 

 

 

 

lim

 

 

 

 

.

 

 

x→0

 

 

tg(23 x )

 

 

 

x→0

ex −

1

 

 

 

184

15.1.4. a) lim

1− cos (1− cos x)

;

 

 

 

b) lim

x2 + e

x

 

− 1

.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x→0

 

 

arcsin x2

 

 

 

 

 

 

 

 

x→0

 

 

 

x

 

 

 

 

 

 

 

 

 

 

15.1.5. a) lim

 

 

 

2 −

 

1+ cos x

 

;

 

 

 

 

 

b)

lim

 

 

 

2 x+1 − 1

.

 

 

 

 

x→0

 

 

sin2

 

x

 

 

 

 

 

 

 

 

 

 

x→−1 arcsin 3

 

x + 1

 

 

 

 

15.1.6. a)

lim

arcsin 5x − arcsin 3x

;

 

b)

lim

(2 + x)3 − 8

.

 

 

 

 

 

x→0

 

 

arctg2x + arctgx

 

 

 

 

x→0

 

ln 1+ x

)

6

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

(

 

 

 

 

 

 

 

 

 

 

15.1.7. a)

lim

x + tg

 

x − 2 sin x

;

 

 

b)

lim

 

ex

− e−2x

 

.

 

 

 

 

 

 

 

 

 

 

x + x2

+ tg x

 

 

 

 

 

 

 

 

tg x

 

 

 

 

 

 

 

 

 

 

 

x→0

 

 

 

 

 

 

 

 

 

x→0

 

 

 

 

 

 

 

 

 

 

 

 

 

 

15.1.8. a)

lim

 

 

1+ arcsin x −

 

 

1− sin x

; b) lim

ex

− e + ln(2 − x2 )

.

 

 

 

 

 

 

 

 

tg x

 

 

 

 

 

 

 

 

 

 

2x2

−

3x + 1

 

 

x→0

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x→1

 

 

 

 

 

15.1.9. a)

lim

ln(ex

+ x sin x)

 

;

 

 

 

 

 

b)

lim

 

sin(tg5x − tgx)

 

 

 

x→0

 

 

ln(1+ tgx)

 

 

 

 

 

 

 

 

x→0

 

 

arcsin tg2x

 

 

 

 

15.1.10. a) lim

 

sin2 x − x

;

 

 

 

 

 

 

 

b)

lim

 

arcsin(tg x − x)

.

 

 

 

 

x + x

 

 

 

 

 

 

 

 

 

ln(1+ sin x)

 

 

 

 

 

x→0 tg

 

 

 

 

 

 

 

 

 

 

x→0

 

 

 

 

 

 

15.1.11. a) lim

 

 

1+ x sin x − 1

;

 

 

 

 

 

b)

lim

 

ex

− 2− x

.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x

 

 

 

 

 

 

 

 

 

 

sin x

 

 

 

 

 

 

 

 

 

 

 

x→0

 

 

 

tg

2

 

 

 

 

 

 

 

 

 

 

 

x→0

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

15.1.12. a)

lim

 

sin (tg5x − tgx)

;

 

 

 

b)

lim

2

x − cos x

.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x→0

 

arcsin tg2x

 

 

 

 

 

 

 

 

x→0

 

 

 

sin

x

 

 

 

 

 

 

 

 

 

 

15.1.13. a)

lim

 

sin x + sin 2x − sin 3x

;

b)

lim

 

 

2x−1 − 1

 

.

 

 

 

 

 

 

 

3x2

 

 

 

 

 

 

 

 

 

 

 

 

 

− 3x +

2

 

 

 

 

 

 

 

x→0

 

 

 

 

(1+ x)

 

 

x→1 x2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

e

 

 

 

− 1 ln

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

15.1.14. a) lim

 

sin2 (x − 1)

;

 

b)

lim

sin

2 x + sin2 2x − sin2 3x

.

 

 

 

 

 

 

 

 

 

(

 

 

 

 

)

x→1 x2 − 3x + 2

 

 

 

x→0 (e− x

 

 

+ sin x

 

 

 

 

− 1) ln 1

 

 

15.1.15. a) lim

3x2 − 5x

;

 

 

b)

lim

1− cos10x

.

 

 

 

 

 

 

x→0

 

sin 3x

 

 

 

 

x→0

e

x2

− 1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

15.1.16. a) lim

 

tg3x + tgx − sin 2x

;

b)

lim

 

 

3x+1 − 3

 

 

 

.

 

 

 

sin x − sin 5x

ln (1+ x 1+ xe

 

 

)

 

 

x→0

 

 

 

x→0

x

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

185

15.1.17. a)

lim

tg x + ln (1+ 3 x2 )

;

 

 

 

 

 

 

 

 

 

 

3x2

 

 

 

 

x→0

 

sin 3x +

− 1

 

 

 

 

 

 

2

 

 

 

 

15.1.18. a)

lim

 

4x+1

− 4

 

 

;

 

 

 

 

 

 

 

 

 

 

x→0 ln (1− x 1+ x2x )

 

 

15.1.19. a)

lim

2 sin2 x − tg4 x

;

 

 

 

 

 

 

 

 

 

 

x→0 ex2 − 1+ x3

 

 

 

 

15.1.20. a) lim

 

 

1+ x − 1

;

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x→0 sin π (x + 2)

 

 

 

 

 

 

15.1.21. a)

 

 

3tgx − 2x2

+ x4

 

 

lim

 

 

 

 

 

 

;

 

 

 

arcsin 6x

 

 

 

 

x→0

 

 

 

 

 

15.1.22. a) lim

 

 

1− cos 2x

 

 

;

 

 

 

 

 

 

 

 

 

 

 

 

 

x→0 cos 7x − cos 3x

 

 

 

 

15.1.23.a) lim 2x3 − x2 . x→0 ln cos x

15.1.24. a)

lim

1− cos 4x

;

 

 

 

x→0 cos 5x − cos 4x

 

15.1.25. a)

lim

ln(ex + x2 )

;

 

arcsin 2x

 

 

x→0

 

 

15.1.26. a) lim 1+ x sin x − cos 2x ;

x→0

sin2 x

15.1.27.a) lim ln (9 − 2x2 ) ; x→2 sin 2πx

15.1.28. a) lim

x2

− 3x + 3 − 1

;

 

sin πx

x→1

 

 

15.1.29.a) lim cos (x + 5π 2)tg x ; x→0 arcsin 2x

186

 

 

5x−3

2x2

 

b) lim

3

− 3

.

 

 

 

 

 

x→1

 

tg πx

 

b) lim

 

ln(1+ 3x) − 2 sin2 x

.

 

 

arctg2x

x→0

 

 

 

b)

lim

ln (5x − 19)

.

 

 

 

 

 

 

 

 

 

 

 

x→4

x2 − 5x + 4

 

 

 

b)

lim

 

ln (1+ x2 )

.

 

 

 

 

 

 

 

 

 

 

 

x→0 1−

x2 + 1

 

 

 

b)

lim

2cos2 x − 1

.

 

 

 

 

ln sin x

 

 

 

 

 

 

 

 

x→

π

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

b)

lim

 

2(eπx − 1)

.

 

 

 

 

 

 

 

1)

 

 

x→0 3(3 1+ x −

 

 

 

b)

lim

 

 

 

x2 − 9

 

.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x→3 esin π x − 1

 

 

 

 

 

 

b)

lim

 

 

3x+1 − 3

 

 

.

 

 

 

1+ xex )

 

x→0 ln(1+ x

 

b)

lim

 

 

x2 (ex − e− x )

 

.

 

 

 

ex3 − 1

 

 

 

 

 

 

x→0

 

 

 

 

 

 

 

b)

lim

 

2x

+ 4 x

 

− 2

.

 

 

arctg

 

x

 

 

 

 

 

x→0

 

 

 

 

 

 

 

b)

lim

 

2(eπx − 1)

.

 

 

 

 

 

3 8 + x −

2

 

 

 

 

 

x→0

 

 

 

 

 

 

b)lim ln(ex + x sin x) . x→0 ln(1+ sin x)

b)

lim

2x

− 1

 

.

(

+ 2x

)

 

x→0 ln 1

 

 

15.1.30. a) lim

(1+ 2x)6 − (1+ x)7

;

b)

lim

 

eπx − 1

 

.

sin 2x

(

+ arcsin x

)

x→0

 

 

 

 

 

 

x→0 ln 1

 

 

15.2. Compare infinitesimals

15.2.1. α(x) = x − x2 − x , 15.2.2. α(x) = x3 − 3x + 2 ,

15.2.3. α(x) =

1

,

x2 + 3x

 

 

15.2.4. α(x) =

x − 2 ,

 

15.2.5. α(x) = x3 + x − 2 , 15.2.6. α(x) = 1− 2 cos x ,

15.2.7.α(x) = x3 + 2x − 12 ,

15.2.8.α(x) = ctg x ,

15.2.9. α(x) = sin( x − 2) ,

15.2.10.α(x) = tg(x3 + x) ,

15.2.11.α(x) = (x3 + 2)−1 ,

15.2.12.

α(x) = sin(x − x ) ,

15.2.13.

α(x) = arcsin(2 − x)

15.2.14.α(x) = ex − 1 ,

15.2.15.α(x) = ln(1+ x ) ,

15.2.16.α(x) = 3 x − 3 ,

15.2.17. α(x) =

x − 2

,

x + 2

 

 

15.2.18.α(x)

15.2.19.α(x)

15.2.20.α(x)

15.2.21.α(x)

15.2.22.α(x)

15.2.23.α(x)

= x sin x ,

=x − sin x ,

=x sin(2 / x) ,

=x2 cos(1/ x) ,

=arctg x ,

x

= arctg x − π2 ,

 

α(x) and β(x) .

 

 

 

 

 

 

β(x) = x + x3 − 3 3 x if

x → 0 .

 

β(x) = x − 2

if x → 2.

 

β(x) =

 

1

if

x → +∞ .

 

x3 − 2x

 

 

 

 

 

 

β(x) = x2 − 16

if

x → 4 .

 

β(x) = x − 1

if x → 1.

 

β(x) = 4x − π

if x → π / 4.

 

β(x) = x2 − 4

if

x → 2.

 

β(x) = π − 2x

if

x → π / 2.

 

β(x) = x −4

if

x → 4 .

 

β(x) = x

 

 

 

if

x → 0 .

 

β(x) = (x10 − 15)−1/ 3 if

x → ∞.

 

β(x) = 2 x

 

 

 

if

x → 0 .

,

β(x) = 4 − x

if

x → 4 .

 

β(x) = x2

 

 

 

if

x → 0 .

 

β(x) = 1+ 3 x − 1

if

x → 0 .

 

β(x) = 27 − x

if

x → 27.

 

β(x) =

x − 4

 

if

x → 4 .

 

 

 

 

 

 

x + 4

 

 

 

β(x) = x3

 

 

 

if

x → 0 .

 

β(x) = x

 

 

 

if

x → 0 .

 

β(x) = x

 

 

 

if

x → 0 .

 

β(x) = x

 

 

 

if

x → 0 .

 

1

 

 

 

 

x → ∞ .

 

β(x) =

 

 

if

 

x − 2

 

β(x) = 1/ x

 

 

 

if

x → +∞ .

187

15.2.24.α(x)

15.2.25.α(x)

15.2.26.α(x)

15.2.27.α(x)

15.2.28.α(x)

15.2.29.α(x)

15.2.30.α(x)

=x2 sin(1/ x) ,

=arcctg(1/ x) ,

=x3 − 8 ,

x

= arcsin(x − 2) , x

=x + 2x2 − 3 x ,

=x2 + 5x + 4 ,

=1− 2 cos x ,

β(x) = x −

x

β(x) = x

 

 

 

β(x) =

x2

− 4

x

+ 2

 

 

 

β(x) = x3 − 8

β(x) = 1−

1− x

β(x) = x2 + 3x + 2

β(x) = (3x − π)2

if x → 0 . if x → 0 .

if x → 2 .

if x → 2 .

if x → 0 . if x → −1. if x → π / 3 .

Micromodule 16

BASIC THEORETICAL INFORMATION

CONTINUITY OF A FUNCTION

Continuity of a function at a point. Classification of points of discontinuity.

Literature: [3, chapter 2, п.п. 2.1—2.5], [4, section 4, п. 4.3], [6, chapter 4, § 5], [7, chapter 4, § 13], [10, chapter 3, § 5], [11, chapter 3, § 4], [12, chapter 1, §§ 6—8, chapter 2, §§ 9—10], [13].

16.1. Continuity of a function at a point

Definition 3.18. A function f (x) is said to be continuous at point x = c if it satisfies three conditions:

1)the function f (x) is determined at this point and in its neighbourhood;

2)there exists a limit of the function if x → c;

3)this limit is equal to the value of the function at the point c , i.e.

у

 

 

 

f(x)

 

∆y

y = f(x)

 

f(x0)

 

 

 

∆x

 

 

 

 

 

 

О

 

х0 х

х

 

 

Fig. 3.10

 

188

 

 

 

x→c

(

x

)

= f

(

c

)

(3.6)

lim f

 

 

 

 

If the condition (1) is performed, the conditions

(2) and (3) are equivalent to such an expression as:

lim y = 0 ,

(3.7)

x → 0

where y= f (x0 + x)− f (x0 ).

Functions continuity at a point possesses the following properties:

1) a sum, a difference, a product of a finite number of functions, continuous at a point c , is a function, continuous at this point;

2) The ratio of two functions ϕf ((xx)) , continuous at a point c , is a function, continuous at this point provided ϕ (c) ≠ 0 ;

3)a composite function formed from a finite number of continuous functions is continuous;

4)a function inverse to a monotone continuous function is continuous.

The basic elementary functions are continuous at all points where they are determined. So from properties of continuous functions the next important conclusion follows: any elementary function is continuous at each point where it is determined.

If one of conditions (1—3) of continuity of a function is not carried out at a point c then the point c is said to be a point of discontinuity of the function

y = f (x).

16.2. Classification of points of discontinuity

We have to distinguish three cases:

i) the limit of a function at point c exists, but the function is not determined

at this point or lim f (x) ≠ f (c) then c is said to be a point of removable

x→c

discontinuity;

ii) there exist finite limits of the function from the left and from the right but f (c − 0) ≠ f (c + 0) then this point c is said to be a point of essential discon-

tinuity or of the first kind;

iii) there do not exist finite limits of the function from the left or from the right at the point x = c (in particular, c may be equal to infinity) then c is said to be a point of infinite discontinuity or of the second kind.

Micromodule 16

EXAMPLES OF PROBLEMS SOLUTION

Example 1. Investigate the function for continuity:

f (x) =

x + 2

 

.

3x2 + 5x − 2

Solution. The function is determined on all the numerical axis, except the points where a denominator is equal to zero, i.e.

3x2 + 5x − 2 = 0 .

189

Solving this equation we obtain:

 

 

 

 

 

 

x =

− 5 ± 25 + 24

=

−5 ± 7

,

 

 

 

 

 

 

6

6

 

 

 

 

 

 

 

 

 

i.e.

x

= −2 x

2

=

1

. They are points where the function is not determined i.e. it

 

 

1

 

3

 

 

 

 

 

has discontinuities. We have to find the limits of the function at these points:

lim

x + 2

= lim

x + 2

 

= −

1

,

 

(3x − 1)(x + 2)

7

x→−2 3x2 + 5x − 2

x→−2

 

 

i.e. the point x = −2 is a point of removable discontinuity.

Having accepted

f (−2) = − 1 we shall get a continuous function.

For x = 1

 

 

7

 

 

 

 

 

 

 

we have:

 

 

 

 

 

 

 

 

 

2

3

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

lim

 

x + 2

 

=

lim

 

1

 

= + ∞ ;

 

 

 

3x2 + 5x − 2

 

3x − 1

 

 

x→ 1 +0

 

x→ 1 +0

 

 

 

 

 

3

 

 

 

 

3

 

 

 

 

 

 

 

lim

 

x + 2

=

lim

1

 

= − ∞ ,

 

 

 

 

3x2 + 5x − 2

3x − 1

 

 

 

x→ 1 −0

 

 

x→ 1 −0

 

 

 

 

3

 

 

 

 

3

 

 

 

 

i.e., the point

x = 1

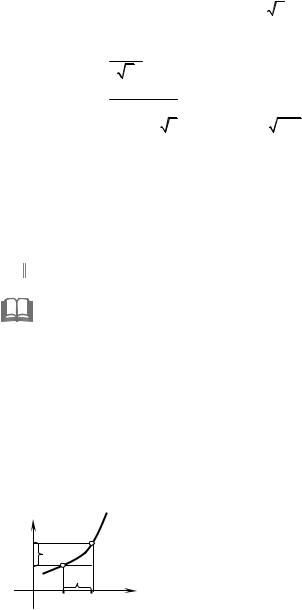
is a point of infinite discontinuity. The graph of this func-

3

tion is represented on Fig. 3.11.

5

3

1

– 3

– 1 –1

1

3

–3

–5

Fig. 3.11

190

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
Помощь Обратная связь Вопросы и предложения Пользовательское соглашение Политика конфиденциальности