Higher_Mathematics_Part_1

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный авиационный университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Α1 A2 + B1Β2

.pdf

Скачиваний:

1052

Добавлен:

19.02.2016

Размер:

6.63 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 910 / 2810 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

tg ϕ =|tg(α

− α ) |=

tg α2 − tg α1

k2 − k1

(2.7)

1+ tg α1 tg α2

1+ k1k2

α1

α2

Fig. 2.3

Fig. 2.4

If two straight lines

are parellel then ϕ = 0,

tg ϕ = 0,

k2 − k1 = 0.

Therefore the condition of parallelism of two straight lines is

k1 = k2 .

(2.8)

If two straight lines L

are perpendicular then

ϕ =

tg ϕ does not

exists, so 1+ k1k2

= 0

the formula (2.7). Therefore

the condition of per-

pendiculariry is:

= −

(2.9)

Let two straight

lines

і L2

given by

their general

equations

Α1 x + Β1 y + C1 = 0

and Α2 x + Β2 y + C2 = 0. Then

1) the angle between these straight lines is equal to the angle between their normal vectors nG1 = { Α1 , Β1} аnd nG2 = { Α2 , Β2} . This angle is determined from the equality:

2) the condition of parallelism of straight lines is:

Α1 = Β1 ; Α2 Β2

3) the condition of perpendicularity is:

Α1 Α2 + Β1Β2 = 0.

7.8. Distance from a point to a straight line

Let a straight line L be given by the equation

Αx + Βy + C = 0 and a point

M0 (x0; y0 ) be given too (Fig. 2.4).

A distance d from the point M

to the straight line L equals the module of a

JJJJJJJG

projection of the vector Μ1Μ0

where M1(x1; y1) is any point of the straight line

L onto the direction of a normal vector

n =

{

}

Α; Β .

JJJJJJJG

| (x

− x ) A + ( y

− y ) B |

| Μ

n |

d =| прnG Μ1Μ0 |=

1 G

| n |

+ B

| Ax0 + By0 − (Ax1

+ By1 ) |

| Ax0

+ By0

+ C |

A2 + B2

So a distance from a point to a straight line may be found by the formula

d =

Αx0 + By0 + C

(2.10)

Α2 + B2

Micromodule 7

EXAMPLES OF PROBLEMS SOLUTION

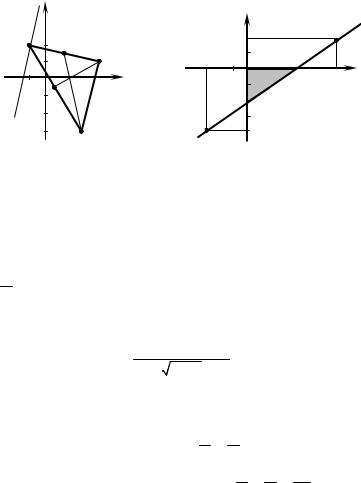
Example 1. Given points A(3; 1) , B(2; −3), C(−1; 2) are vertices of a

triangle ABC. Form:

а) a general equation of the side AB;

b)a symmetric equation of the height AD;

c)parametric equations of the median ВМ;

d)an equation of a straight line passing through the point C(−1; 2) and paral-

lel to the side AB.

Solution. Let us construct a triangle ABC (Fig. 2.5) and consider the following cases.

а) As we know coordinates of the points A and B we can get the equation of the side AB according to the formula (2.4):

x − 3	=	y − 1	, or	x − 3	=	y − 1	, or y −1 = 4(x −3) .

2 − 3		−3 − 1		−1		−4

Whence 4x − y − 11 = 0. The latter is a general equation of the straight line

containing the side AB.

b) To write down symmetric equations of a straight line it is necessary to know a point lying on the straight line, and its direction vector. The vector

SΑΟΒ

JJJG

BC = {−3; 5} for the height AD is a normal vector then the vector a = {5; 3} will

be perpendicular to the vector BC

JJG

= 0 ). Now we

(as their dot product BC a

can write down the symmetric equation of the straight line AD:

x − 3

y − 1

c) As the point M is a midpoint of the line segment АС then

x = 3 − 1

= 1,

= 1+ 2

= 1,5 .

JJJJG

− 2; 1,5

+ 3}

= {−1; 4,5} is a

direction

vector of the

The vector BM = {1

straight line	BM . For the direction vector it is also possible to take a vector
JJJJG		, m	= 9		and the parametric equations of the
a = 2BM = {−2; 9} . So l = −2
median may be written as:
	x = 2 − 2t,				t R.
		= −3	+ 9t	,
	y

d) So as a straight line passes through the point C(−1; 2) and is parallel to the side AB we can take a normal vector n = {4; − 1} of the straight line АВ

for the normal vector of the required straight line. Then the required equation looks like

4(x +1)−( y −2) = 0 , or 4x − y +6 = 0 .

Example 2. Calculate the area of a triangle bounded by a straight line passing through two points Μ1 (−3;−4) and Μ2 (6; 2) , and axes of coordinates

(Fig. 2.6).

Solution. Using the formula (2.4), we shall make an equation of a straight line passing through the points Μ1 (−3;−4) and Μ2 (6; 2) :

x + 3

y + 4

x + 3

y + 4

x + 3

y + 4

6 + 3

2 + 4

2(x +3) = 3( y +4),

2x −3y −6 = 0 .

The latter formula is the general equation of

straight line Μ1Μ2 .

Let us find coordinates of intersection points of the straight line with the coordinate axes.

Let х = 0, then 3b + 6 = 0, or b = −2. If y = 0, then 2a − 6 = 0, or a = 3.

So the straight line intersects the axis Ox at the point A (3; 0), and the axis Оу at the point B(0; −2). Lengths of legs in the triangle AOB are OΑ= 3, OB = 2 respectively, then the area of the triangle is:

= 3 sq. units.

M А

–3

6 х

–4

Fig. 2.5

Fig. 2.6

Example 3. Find distance between straight lines

4x − 3y + 2 = 0 and 8x −

−6y −13 = 0 .

Solution. So as the given straight lines are parallel, distance between them is constant and equal to distance from any point of the second straight line to the first. We take any point on the straight line 8x −6y −13 = 0. Let x = 0 , then

y = − 136 . Distance from the point M(0; −13/ 6) to the straight line 4x − 3y + 2 = 0 may be found by the formula (2.9):

4 0 − 3 (− 13) + 2

d = 6 = 1,7. 16 + 9

Example 4. Find m and n for which straight lines mx + 8y + n = 0 and 2x + my − 1 = 0 а) are parallel; b) coincide; c)are perpendicular.

Solution. а) Condition of parallelism is: m2 = m8 , whence m2 =16 , m = ±4 ;

b) The straight lines coincide if the condition m2 = m8 = −n1 holds.

From this we receive two pairs of values m = 4, n = −2 or m = −4, n = 2 .

c) Condition of perpendicularity of straight lines is m × 3 + 8 × m = 0, that is m = 0 .

Answers: а) m = ±4 , n R ; б) m = 4, n = −2 ; m = −4, n = 2 ; c) m = 0 , n R .

Example 5. Find a point symmetric to the point P (−8; 12) relative to the straight line 4x +7 y +13 = 0 .

Solution. Let Q(xQ , yQ ) be the required point (Fig. 2.7). The problem may be solved in such a sequence:

Р(–8; 12)

n ={4; 7}

Fig. 2.7

1)we make equations of a straight line РО passing through the point Р and perpendicular to the straight line L;

2)we find an intersection point O of the straight lines L and РО. It is a projection of the point Р onto the straight line L;

3)we determine coordinates of the point Q, taking into account that the point O is a midpoint of PQ.

The normal vector of the straight line L at the same time is a direction vector of the perpendicular РО, therefore the symmetric equation of the straight line РО has such a form:

x +8 = y −12 , 4 7

whence we receive 7(x +8) = 4( y −12), 7x −4 y +104 = 0. Having solved the system of equations

7x − 4x + 104 = 0,4x + 7x + 13 = 0,

we can find coordinates of the intersection point of straight lines: xO = −12, yO = 5.

Connection between coordinates of points P, O and Q is well known:

x =	xP + xQ		,	y =		yP + yQ		.

O		2		O	2
Then
		−8 + xQ				12 + yQ
−12 =				, 5 =			,
		2			2

whence we receive coordinates of the symmetric point: xQ = −16, yQ = −2.

Micromodule 7

CLASS AND HOME ASSIGNMENTS

1. Sketch graphs of straight lines y = 3x − 2 and x + 2 y − 3 = 0 , and find a point of their intersection.

2.The area of a triangle АВС is 8, two its vertices are points A (0; –3) and B (1; 2). Find coordinates of the vertex C if it lies on the straight line y = 3 .

3.Let the points A(0; –4), B (3; 2), C(–5; 1) be vertices of a triangle. Find: а) a general equation of the side AB;

b)a symmetric equation of the height AD;

c)a parametric equation of a median BM;

d)distance of a vertex B to the median AM.

4.Find projection of a point Р (–7; 11) onto a straight line passing through

points A (3;−4) and B(−4; 0).

5. Show that straight lines 5x −12y +13, 5 = 0 and 10x −24 y = 25 are

parallel and find distance between them.

6. Let a point A (3; 4) be a vertex of a rectangular triangle. A = 45° and x − y + 2 = 0 is an equation of the leg opposite to the vertex A. Find equations

of two other sides of the triangle.

7. An equation of a straight line 3x +2 y +7 = 0 is given. Find equations of

straight lines passing through the point M (–2; 0), and: а) parallel to the given straight line;

b) perpendicular to the given straight line.

Answers	x		y +4
2. С (–2; 3) or (4,4; 3). 3. а) 2x −y −4 = 0 ; b)		=		. 4. (–11; 4).
	1		−8

5. 2. 7. а) 3x + 2 y +6 = 0 ; b) 2x −3y +4 = 0 .

Micromodule 7

SELF-TEST ASSIGNMENTS

7.1. Given points M1 , M2 , M3 are vertices of a triangle M1M2 M3 . Find

a)a general equation of the side M1M2 ;

b)a symmetric equation of the height M1D ;

c)a parametric equations of the median M2 M ;

d)an equation of a straight line passing through the point M3 and parallel to

the side M1M2 .

e) a projection of the point M1 onto the straight line M2 M3 .

7.1.1. M1 (0; 1) ,	M2 (6; 3) ,		M3 (−1; 0) .
7.1.2. M1 (0; 6) ,	M2 (1; −3) ,		M3 (−2; 3) .
7.1.3. M1 (6; −2) ,	M2 (−4; −1) ,		M3 (0; −2) .
7.1.4. M1 (2; 2) ,	M2 (−1; 7) ,		M3 (1; 4) .
7.1.5. M1 (1; 8) ,	M2 (0; −3) ,		M3 (−1; 2) .
7.1.6. M1 (−5; −1) ,	M2 (−3; 0) ,		M3 (1;−2) .
7.1.7. M1 (0;−2) ,	M2 (−3; 6) ,		M3 (5; 3) .
7.1.8. M1 (3;−2) ,	M2 (2; 7) ,		M3 (−2;1) .
7.1.9. M1 (0; 5) ,	M2 (11;−5) ,		M3 (−1;−1) .
7.1.10. M1 (1; 0) ,	M2 (6;1) ,		M3 (3;−2) .
7.1.11. M1 (−1; 4) ,	M2 (11; 5) ,		M3 (0; 1) .
7.1.12. M1 (4; 6) ,	M2 (−6; 3) ,		M3 (−2; 0) .
7.1.13. M1 (2;−1) ,	M2 (5; 0) ,		M3 (−2;−2) .
7.1.14. M1 (−4; 5) ,	M2 (2; 0) ,		M3 (−2;−2) .
7.1.15. M1 (7; 5) ,	M2 (−1; 2) ,		M3 (1;−1) .
7.1.16. M1 (3; 2) ,	M2 (3; 5) ,		M3 (1;−1) .
7.1.17. M1 (−3; 9) ,	M2 (7;−2) ,		M3 (3; 3) .
7.1.18. M1 (0;1) ,	M2 (6; 4) ,		M3 (−1; 0) .
7.1.19. M1 (2;−4) ,	M2 (4;−2) ,		M3 (0; 2) .
7.1.20. M1 (5;−7) ,	M2 (−5; 1) ,		M3 (−1;−1) .
7.1.21. M1 (1; 3) ,	M2 (3; 2) ,		M3 (5; 0) .
7.1.22. M1 (−1;−2) ,	M2 (2;−1) ,		M3 (0;−1) .
7.1.23. M1 (7; 1) ,	M2 (−1; 0) ,		M3 (−2; 3) .
7.1.24. M1 (0;1) ,	M2 (−1; 4) ,		M3 (6; 0) .
7.1.25. M1 (−4;−9) ,	M2 (6;−1) ,		M3 (2;1) .
7.1.26. M1 (−1; 1) ,	M2 (2;−6) ,		M3 (1; 2) .
7.1.27. M1 (1; 2) ,	M2 (−2; 1) ,		M3 (−4; 3) .
7.1.28. M1 (−1; 4) ,	M2 (−5; 1) ,		M3 (1;−1) .
7.1.29. M1 (3;−4) ,	M2 (−2; 5) ,		M3 (0; 4) .
7.1.30. M1(13; −3),	M2 (2; 5) ,		M3 (−2;1) .
7.2. Find the distance between straight lines
7.2.1. 2x +5y −12 = 0	and	4x +10y −11 = 0 .
7.2.2. 3x −4 y −7 = 0	and	−6x +8y −15 = 0 .
7.2.3. 2x −5y −11 = 0	and	−6x +15y −17 = 0 .
7.2.4. 3x −7 y −7 = 0	and	12x −28y −25 = 0 .

7.2.5. 5x +6y +22 = 0	and	10x +12 y −31 = 0 .
7.2.6. x −7 y −32 = 0	and	2x −14 y −13 = 0 .
7.2.7. 3x +5y +5 = 0	and	9x +15y −17 = 0 .
7.2.8. 3x −8y −27 = 0	and	−6x +16 y +11= 0 .
7.2.9. 2x −9y −37 = 0	and	−6x +27 y −10 = 0 .
7.2.10. 3x −4 y −18 = 0	and	15x −20 y −41 = 0 .
7.2.11. x +6y −14 = 0	and	4x + 24 y −23 = 0 .
7.2.12. 3x −7 y −8 = 0	and	9x −21y −16 = 0 .
7.2.13. 3x −5y −19 = 0	and	6x −10 y −21 = 0 .
7.2.14. −3x −4 y −28 = 0	and	9x +12 y +7 = 0 .
7.2.15. 4x −3y +7 = 0	and	8x −6y −11 = 0 .
7.2.16. 5x −4y −48 = 0	and	15x −12y −5 = 0 .
7.2.17. 5x +3y −43 = 0	and	20x +15y +22 = 0 .
7.2.18. 7x −2 y −15 = 0	and	14x −4 y −5 = 0 .
7.2.19. 3x −y −6 = 0	and	15x −5y −32 = 0 .
7.2.20. 3x +7 y + 42 = 0	and	12x + 28y −61 = 0 .
7.2.21. 6x +7 y +16 = 0	and	12x +14 y −21 = 0 .
7.2.22. 8x −5y +32 = 0	and	16x −10y −17 = 0 .
7.2.23. 6x +11y +22 = 0	and	18x +33y −43 = 0 .
7.2.24. 3x +10 y +27 = 0	and	9x +30y −11 = 0 .
7.2.25. 4x −7 y +35 = 0	and	12x −21y −62 = 0 .
7.2.26. −3x +5y + 4 = 0	and	18x −30y −1 = 0 .
7.2.27. 2x +5y +12 = 0	and	10x +25y −13 = 0 .
7.2.28. −4x +3y +17 = 0	and	12x −9y −22 = 0 .
7.2.29. 5x +7 y +16 = 0	and	15x +21y −44 = 0 .
7.2.30. 11x +5y +15 = 0	and	22x +10y −7 = 0 .

7.3. Find the area of a triangle cut off from the coordinate angle by a straight line:

7.3.1. 4x +5y −40 = 0 .	7.3.2.	4x −5y +25 = 0 .
7.3.3. 5x +8y −35 = 0 .	7.3.4.	6x −11y −128 = 0 .
7.3.5. 3x +13y −195 = 0 .	7.3.6.	2x +7 y −140 = 0 .
7.3.7. 7x −12y −168 = 0 .	7.3.8.	7x +5y −140 = 0 .
7.3.9. 13x +5y −260 = 0 .	7.3.10. 4x +7 y −560 = 0 .
7.3.11. 3x +7 y −210 = 0 .	7.3.12. 8x +13y −208 = 0 .
7.3.13. 6x −7 y −210 = 0 .	7.3.14. 9x + 4 y −180 = 0 .

7.3.15.	2x +7 y −35 = 0 .	7.3.16. 9x +7 y −126 = 0 .
7.3.17.	4x − 7 y − 420 = 0 .	7.3.18. 3x +11y +132 = 0 .
7.3.19.	4x + 5y + 45 = 0 .	7.3.20. 6x +7 y +21 = 0 .
7.3.21. 5x −7 y −175 = 0 .		7.3.22. 8x −5y +50 = 0 .
7.3.23. 6x +13y +130 = 0 .		7.3.24. 5x +8y +75 = 0 .
7.3.25. 3x +5y +80 = 0 .		7.3.26. 4x +9 y +81 = 0 .
7.3.27. 3x − 13y − 169 = 0 .		7.3.28. 9x +5y +75 = 0 .
7.3.29.	4x + 11y + 121 = 0 .	7.3.30. 5x −8y −64 = 0 .

7.4.Determine values m and n for which straight lines are: а) parallel; b) coincident; c) perpendicular.

7.4.1. mx + 6y + n = 0	and	3x + my-2 = 0.
7.4.2. mx + 7y + n = 0	and	2x + my – 5 = 0.
7.4.3. (m + 1)x + 5y + 2n = 0	and	3x + my – 4 = 0.
7.4.4. (m – 2)x + 3y + n + 2 = 0	and	x – my – 2 = 0.
7.4.5. (m + 4)x + 2y + n – 1 = 0	and	2x + my – 6 = 0.
7.4.6. (m – 4)x – y + n – 2 = 0	and	3x + my – 5 = 0.
7.4.7. (m + 2)x + 4y + n – 3 = 0	and	3x – my + 4 = 0.
7.4.8. (m + 5)x + 4y + n + 1 = 0	and	x + 2my – 3 = 0.
7.4.9. m x + 3 y + n – 3 = 0	and	3x + (m + 1)y – n = 0.
7.4.10. (m – 2)x + 5y + n – 4 = 0	and	x – (m + 1)y – 6n = 0.
7.4.11.. (m – 3)x + y + n – 4 = 0	and	x – (m + 1)y – 6n = 0.
7.4.12. (m + 3)x + 2y + n – 5 = 0	and	2x – (m + 2)y – 4n = 0.
7.4.13. (m – 1)x + y + n + 2 = 0	and	3x – (m – 1)y – 2n = 0.
7.4.14. (m – 2)x + 3y + n – 3 = 0	and	x + (m + 1)y + 2n = 0.
7.4.15. (m + 3)x + 2y + 2n – 1 = 0	and	x – my – 6 + n = 0.
7.4.16. (m – 1)x + 4y + 3n – 4 = 0	and	x – (m + 2)y – n = 0.
7.4.17. (m – 3)x + y + n – 4 = 0	and	x – (m + 1)y – 6n = 0.
7.4.18. ( m – 5)x + 2y + 2n – 3 = 0	and	x – (m + 2)y – n – 1 = 0.
7.4.19. ( m + 2)x + y – n – 4 = 0	and	x + (m + 1)y + 2n = 0.
7.4.20. ( m + 1)x – y + n – 3 = 0	and	x – (m – 1)y – 3n = 0.
7.4.21. ( m – 6)x – y + n – 2 = 0	and	x + (m + 2)y – n – 1 = 0.
7.4.22. mx + 2y + 3n – 2 = 0	and	x – (m + 4)y – 2n = 0.
7.4.23. mx – y + 2n – 5 = 0	and	x + (m + 2)y + n = 0.
7.4.24. (m – 1)x – y + 2n – 1 = 0	and	2x – my – n + 1 = 0.
7.4.25. (2m – 1)x + y-n – 3 = 0	and	x – (m + 1)y – n = 0.
7.4.26. mx – y + 3n – 1 = 0	and	x – (m – 1)y – n – 1 = 0.

7.4.27. (m – 3)x – y + 2n – 4 = 0	and	x + my – n + 1 = 0.
7.4.28. mx + 2y + n – 2 = 0	and	x + (m + 2)y + 2n – 1 = 0.
7.4.29. (m – 1)x + 2y + n = 0	and	x – (m – 1)y – n – 2 = 0.
7.4.30. mx + 3y + 2n – 1 = 0	and	x + (m + 3)y + n = 0.
Micromodule 8
BASIC THEORETICAL INFORMATION. PLANE

General equation of a plane, incomplete equations. An equation of a plane passing through three points. An equation of a plane in segments on axes. A normal equation of a plane, the distance from a point to a plane. An angle between two planes, conditions of parallelism and perpendicularity of planes.

Literature: [1, chapter 8, item 8.2, 8.3], [4, item 3, item 3.5], [6, chapter 3, § 4], [7, chapter 2, § 6], [10, chapter 2, § 2], [11, chapter 2, § 2].

	8.1. General equation of a plane
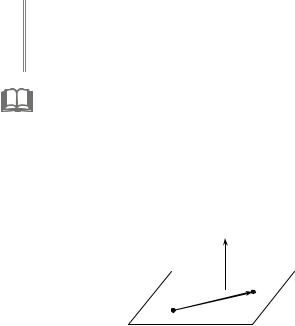
Only one plane passes through the point Μ0 (x0			, y0 ,	z0 ) perpendicularly to
the vector nG	= { A; B; C} (Fig. 2.8). The vector n		is called a normal vector of
that plane.
		n ={A, B, C}

		М
	М0
		Fig. 2.8
Let us find an equation of this plane. Let Μ(x, y,				z) be any point of the
		JJJJG			−z0} are
plane. Then two vectors nG = { A; B; C} and Μ0Μ ={x −x0 ; y −y0 ; z					−z0} are
perpendicular, so their dot product is equal to zero:
	Α(x − x0 ) + Β( y − y0 ) + C (z − z0 ) = 0.				(2.11)
The equation (2.11) is an equation of a plane passing through the point Μ0
and having	a normal vector n. Removing brackets			and denoting	−Αx0 −
−Βy0 −Cz0 = D we get an equation
100

<<< < Предыдущая 1 2 3 4 5 6 7 8 910 / 2810 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
05.09.2019478.78 Кб6gtfnmТ.docx
#
15.08.2019637.53 Кб2Gulenko.docx
#
12.11.2018765.44 Кб6Hagakure_-_Sokrytoe_v_listve.doc
#
19.02.20166.95 Mб201Higher Mathematics. Part 3.pdf
#
19.02.20169 Mб95Higher_Mathematics_Part_1.pdf
#
19.02.20166.63 Mб1052Higher_Mathematics_Part_1.pdf
#
19.02.20167.48 Mб408Higher_Mathematics_Part_2.pdf
#
19.02.20169.73 Mб45Higher_Mathematics_Part_2.pdf
#
19.02.20167.31 Mб123Higher_Mathematics_Part_2.pdf
#
19.02.20169.11 Mб304Higher_Mathematics_Part_3.pdf
#
19.02.2016694.82 Кб10HiraganaKatakanaWorkSheet (1).pdf