
Higher_Mathematics_Part_1
.pdf
Answer: S ABC |
= 3 |
59 square units, VABCD = 3 cubic units. |
|
2 |
|
Example 3. Prove that vectors a = {2; 1; 3}, b = {2; − 3; 1} and c = {1; 2; 1} form a basis and decompose the vector p = {0; 11; 3} according to this basis.
Solution. We remember that any ordered triple of noncoplanar vectors is the basis in the space. Consequently, the given vectors form a basis if their mixed product is not equal to zero. Let us verify this:
abc = |
2 |
1 |
3 |
|
2 |
−3 |
1 |
= 10 ≠ 0. |
|
|
1 |
2 |
1 |
|
Therefore the vectors a, |
b and c are the basis. |
|
|
|
Any vector p |
is decomposed with respect to the basis a, b and |
c |
as |
|
p = αa + βb + γc, |
where |
α, β, γ are unknown numbers (coordinates |
of |
the |
vector p in the given basis). The vector equation is equivalent to the system of equations (vectors are equal if their corresponding coordinates are also equal):
0 = 2α + 2β + γ,11 = α − 3β + 2γ,3 = 3α + β + γ.
From the last system we can find that α = 1, β = −2, γ = 2. Therefore, p = a − 2b + 2c.
Micromodule 6
CLASS AND HOME ASSIGNMENT
1. Vectors a = {−2; 0; 1} and b = {−1; 4; 5} are given. Find:
a)(2a − 5b)× (a + 2b); b) | (a − b)× (a + 2b) | .
2.Determine the area of ABC and the volume of a pyramid, whose vertices are at points A(2; 4; 5), B(–4; 4; –5), C (5; 0; 3), D(1; 2; 0).
3. Prove that vectors a = {−2; 2; − 1}, |
b = {−2; 1; − 1} and c = {−1; 0; 1} form |
a basis and decompose the vector p = {0; 11; 3} with respect to this basis. |
|
Answers |
|
1. a) {–36; 81; –72}; b) 2 161 . 2. S = 3 |
377, V = 6. |
2 |
|
|
81 |
Micromodule 6
SELF-TEST ASSIGNMENT
6.1. Find a cross product:
6.1.1. (2a + 4b)× (3a − b) , if |
a = {−2; 1; 2}, |
b = {−2; 4; 3}. |
|||
6.1.2. (5a + 2b) × (2a − 3b) , if |
a = {−1; 3; 4} , |
b = {−5; 1; 2}. |
|||
6.1.3. (−2a + 7b)× (3a − 2b), |
if a = {−4; 3; 1}, |
b = {2; 2; 1}. |
|||
6.1.4. (3a + 4b) × (2a − b), if |
a = {2; − 3; 4}, |
b = {−1; − 1; 3}. |
|||
6.1.5. (a − 4b)× (2a − 3b), if |
a = {3; 3; 1}, b = {−2; − 3; − 2}. |
||||
6.1.6. (−a + 3b) × (2a + b), if |
a = {−4; 3; 2}, |
b = {−2; 4; 5}. |
|||
6.1.7. (3a + 2b) × (2a − 6b), if |
a = {−1; 0; 4}, |
b = {−3; 1; 2}. |
|||
6.1.8. (−3a + 7b)× (3a − b), |
if |
a = {4; 3; 2}, |
b = {2; 1; 4}. |
||
6.1.9. (−3a − 2b)× (2a + b), |
if |
a = {0; − 4; 4}, |
b = {−2; − 3; 3}. |
||
6.1.10. (5a − 4b) × (2a − b), if |
a = {3; 2; 1}, |
b = {−1; − 2; − 2}. |
|||
6.1.11. (− a + 4b)× (a + b), |
if |
|
a = {−5; 2; 1}, |
b = {−3; 4; 3}. |
|
6.1.12. (3a − 2b)× (2a − 3b), |
if a = {−1; 4; 4}, |
b = {3; 1; − 2}. |
|||
6.1.13. (−3a − 4b) × (a − b), |
if |
a = {2; 3; 2}, |
b = {2; − 1; − 4}. |
||
6.1.14. (−3a + 2b)× (2a + 9b), |
if a = {0; − 2; 2}, b = {−2; − 3; 0}. |
||||
6.1.15. (5a − 3b)× (a − 3b), |
if |
a = {3; − 2; 1}, |
|
b = {−1; − 2; 2}. |
|
6.1.16. (− a + 3b)× (a + 2b), |
if |
a = {−2; 4; 2}, |
b = {−3; 0; 3}. |
||
6.1.17. (3a − 2b)× (3a + 2b), |
if a = {−1; 2; 3}, |
b = {4; 1; − 3}. |
|||
6.1.18. (3a − b) × (4a − b), if |
a = {2; 1; 2}, b = {2; − 1; − 2}. |
||||
6.1.19. (−3a + b)× (2a + b), |
if |
a = {0; − 2; 1}, |
b = {−2; − 4; 0}. |
||
6.1.20. (2a − 3b)× (a − 2b), |
if |
a = {3; − 2; 0}, |
b = {1; − 2; 2}. |
||
6.1.21. (−a − 2b) × (−a + 2b), if a = {−2; 4; 3}, b = {−3; 0; 2}.
6.1.22. |
(3a − 2b)× (a + 2b), if a = {−1; 2; 1}, b = {4; 1; − 2}. |
6.1.23. |
(2a − b) × (3a + b), if a = {2; 1; 4}, b = {2; − 1; − 3}. |
6.1.24. (−3a + 2b) × (4a + b), if a = {0; − 2; 2}, b = {−2; 3; 0}.
6.1.25. |
(2a − b)× (5a − 2b), if |
a = {4; − 1; 0}, b = {1; − 2; 3}. |
6.1.26. |
(−a − 2b) × (−a − 3b), |
if a = {−2; 4; 0}, b = {−4; 0; 2}. |
6.1.27. (3a − b)× (a + b), if a = {−1; 4; 1}, b = {3; 1; − 2}.
82
6.1.28. (a − b)× (3a + 4b), if a = {2; 0; 4}, b = {3; − 1; − 2}.
6.1.29. |
(3a + 2b)× (4a + b), |
if |
a = {0; − 1; 1}, |
b = {−2; − 1; 0}. |
6.1.30. |
(2a − 3b) × (2a − b), |
if |
a = {3; − 2; 0}, |
b = {1; − 4; 3}. |
6.2. Determine the area of the ABC and the volume of a pyramid ABCD, whose vertices are at the points:
6.2.1. A(1; –2; 3), B(2; 4; 7), C(–3; –4; 0), D(1; 0; 5).
6.2.2. A(–3; 5; 4), B(0; 0; 8), C(–1; 3; –2), D(2; 6; 1).
6.2.3. A(0; –5; 4), B(3; 5; 1), C(–4; –4; 1), D(3; 1; 6).
6.2.4.A(–2; 0; 2), B(1; 0; 6), C(–5; 4; –1), D(0; 4; 2).
6.2.5.A(2; 1; 7), B(–1; 3; 5), C(5; –4; 1), D(2; 5; 1).
6.2.6.A(3; –3; 0), B(4; 4; 2), C(–5; –3; 0), D(1; 1; 4).
6.2.7.A(–4; 6; 4), B(3; 10; 8), C(1; 4; –2), D(–2; 3; 1).
6.2.8.A(0; –3; 5), B(–3; –1; 1), C(2; –5; 2), D(4; 3; 6).
6.2.9.A(–5; 0; 3), B(2; 1; 5), C(–4; 2; –1), D(0; 0; 3).
6.2.10.A(2; 3; 5), B(–1; –3; 4), C(4; –3; 2), D(1; 6; 1).
6.2.11.A(2; –2; 0), B(5; 3; 2), C(–3; –2; 0), D(1; 2; 3).
6.2.12.A(–3; 5; 4), B(2; 8; 7), C(1; 3; –2), D(–1; 4; 1).
6.2.13.A(0; –2; 4), B(–2; –2; 1), C(3; –3; 2), D(3; 3; 4).
6.2.14.A(–3; 2; 3), B(3; 1; –5), C(4; –2; –1), D(4; 0; 3).
6.2.15.A(–2; 3; –5), B(1; 3; 4), C(4; 3; 2), D(1; –6; 1).
6.2.16.A(1; –3; 0), B(4; 3; 1), C(–4; –3; 0), D(–1; –2; 3).
6.2.17.A(3; –5; 4), B(2; 6; –7), C(–1; 3; 2), D(–1; –4; 1).
6.2.18.A(1; 0; 4), B(2; –2; –1), C(3; –1; 0), D(3; 2; 5).
6.2.19.A(–4; 1; 3), B(3; 2; –7), C(2; –1; –1), D(5; 1; 3).
6.2.20.A(–1; 5; –3), B(0; 3; 2), C(1; 3; 4), D(2; –3; 0).
6.2.21.A(–1; –2; 0), B(–4; 3; –1), C(4; –4; 0), D(1; –2; 4).
6.2.22.A(2; –1; 4), B(2; 3; –5), C(–2; 2; 3), D(–2; –3; 1).
6.2.23.A(1; 2; 5), B(2; –3; 1), C(4; –2; 0), D(3; 3; 6).
6.2.24.A(–1; 2; 4), B(0; 2; –6), C(2; –3; 2), D(6; –1; 0).
6.2.25.A(1; –5; –3), B(1; 3; 0), C(–1; 3; –4), D(3; –3; 2).
6.2.26.A(–2; –4; 0), B(4; –3; –1), C(3; –2; 0) D(2; –1; 5).
6.2.27.A(2; –3; 5), B(1; 3; –4), C(–1; 2; 4), D(–1; –5; 2).
6.2.28.A(2; 2; 2), B(3; –3; 4), C(4; –5; 1), D(3; 2; 1).
6.2.29.A(–2; 3; 5), B(1; 2; –4), C(3; –4; 2), D(3; –2; 5).
6.2.30.A(2; –4; –4), B(2; 3; 1), C(–3; 4; –4), D(4; –2; 1).
83
6.3. Prove that vectors p, q and r form a basis and decompose a vector x with respect to this basis:
6.3.1.x ={–2; 11; 14}, p ={1; 1; 3}, q ={1; 2; 1}, r ={–4; 1; 1}.
6.3.2.x ={2; –6; –3}, p ={2; 1; 8}, q ={2; –3; 1}, r ={1; –1; 2}.
6.3.3.x ={–12; 13; –4}, p ={1; 2; 3}, q ={1; 4; 1}, r ={5; 1; –3}.
6.3.4.x ={11; 14; 12}, p ={2; 4; 3}, q ={1; 2; –1}, r ={4; 4; 5}.
6.3.5.x ={–3; –2; 2}, p ={1; 2; 1}, q ={2; 2; –3}, r ={–1; 1; 4}.
6.3.6.x ={–12; –2; –15}, p ={1; 2; –1}, q ={–4; 3; 1}, r ={2; 4; 5}.
6.3.7.x ={–4; 13; 16}, p ={1; 3; 1}, q ={7; –1; 4}, r ={–1; 2; 3}.
6.3.8.x ={4; 5; –7}, p ={1; 2; 1}, q ={2; –1; 1}, r ={–1; 1–3; }.
6.3.9.x ={0; 0; 2}, p ={2; 2; 3}, q ={4; –3; –1}, r ={–6; 1; –1}.
6.3.10.x ={–1; 13; 10}, p ={1; 2; 3}, q ={3; –3; 1}, r ={–2; 4; 1}.
6.3.11.x ={–1; 9; 12}, p ={1; 3; 2}, q ={–2; –1; 3}, r ={3; 2; –1}.
6.3.12.x ={5; –6; 2}, p ={1; 2; 3}, q ={–4; 1; –2}, r ={2; –3; –1}.
6.3.13.x ={16; 2; 10}, p ={2; 1; 1}, q ={–6; 1; –1}, r ={8; –1; 4}.
6.3.14.x ={13; –3; 6}, p ={3; 1; 4}, q ={2; –2; –1}, r ={1; 1; 1}.
6.3.15.x ={13; 16; –1}, p ={1; 2; 1}, q ={2; 3; 1}, r ={–1; 1; 4}.
6.3.16.x ={11; 11; 27}, p ={1; 1; 5}, q ={5; 1; 1}, r ={–1; –5; –1}.
6.3.17.x ={–1; –1; 2}, p ={2; 1; 3}, q ={2; –3; 1}, r ={1; 2; 1}.
6.3.18.x ={1; 2; 6}, p ={1; 2; 3}, q ={1; –3; –1}, r ={–4; 2; –1}.
6.3.19.x ={4; 11; 11}, p ={2; 3; 3}, q ={–1; 4; –2}, r ={–1; –2; 4}.
6.3.20.x ={8; 6; –4}, p ={2; 1; 3}, q ={–1; –3; 1}, r ={1; –5; –7}.
6.3.21.x ={1; 2; 3}, p ={3; 1; 2}, q ={2; 1; 2}, r ={–1; 2; 5}.
6.3.22.x ={10; 8; –2}, p ={1; 6; 3}, q ={6; 3; 1}, r ={3; –1; –6}.
6.3.23.x ={–1; 7; 1}, p ={2; 7; 1}, q ={6; –1; 1}, r ={3; –1; 1}.
6.3.24.x ={–4; 6; 4}, p ={2; 1; 3}, q ={–3; 2; –1}, r ={–3; 4; 2}.
6.3.25.x ={1; 1; 1}, p ={7; 2; –5}, q ={–3; 5; –2}, r ={–3; –6; 8}.
6.3.26.x ={8; 9; 3}, p ={–1; 4; 6}, q ={4; 2; –1}, r ={5; 3; –2}.
6.3.27.x ={0; –9; –3}, p ={3; –2; 6}, q ={4; –3; 1}, r ={5; 5; –1}.
6.3.28.x ={–2; –4; 3}, p ={1; 2; 4}, q ={–4; –3; 1}, r ={2; –1; 2}.
6.3.29.x ={7; 8; 5}, p ={2; 2; 3}, q ={3; 4; –1}, r ={–1; 1; 1}.
6.3.30.x ={–6; 4; –3}, p ={1; 3; 3}, q ={–3; 1; –2}, r ={–3; 3; 2}.
84
Моdule
2
ELEMENTS OF ANALYTICAL GEOMETRY
MODULE STRUCTURE
Micromodule 7. Straight line on a plane. General equation of a straight line, incomplete equations. Symmetric and parametric equations of straight line. Straight line passing through two given points. Equation of a straight line in segments on axes, a slope — intercept form of a straight line. Angle between two straight lines, conditions of parallelism and perpendicularity of two straight lines. Distance from a point to a straight line.
Micromodule 8. Plane in space. General equation of a plane, incomplete equations. Equation of a plane passing through three points. The equation of a plane in segments on axes. Normal equation of a plane, distance from point to the plane. Angle between two planes, conditions of parallelism and perpendicularity of two planes.
Micromodule 9. Straight line in space. Mutual location of a straight line and a plane.
Micromodule 10. Curves of the second order. Circle, an ellipse, a hyperbola, a parabola: definitions, the canonic equations, the basic characteristics.
Micromodule 11. Surfaces of the second order. Cylindrical surfaces. Conic surfaces. Sphere. An ellipsoid. A hyperboloid of one sheet and two sheets. An elliptic and hyperbolic paraboloid. The canonic equations.
Basic concepts. 1. Cartesian rectangular coordinate system. 2. Coordinates of a point. 3. An equation of a line on a plane and in space. 4. An equation of a surface in space. 5. Lines and surfaces of the second order.
Key words: axis — вісь, area — площа, angle — кут, distance — відстань, straight line — пряма лінія, plane — площина, in segments on axes — у від-
різках на осях, parallelism — паралельність, perpendicularity — перпенди-
кулярність, a slope — intercept form of a straight line — рівняння прямої з кутовим коефіціентом, curve — крива, circle — коло, ellipse — еліпс, hyperbola — гіпербола, parabola — парабола, Cartesian rectangular coordinate system — декартова прямокутна система координат, surface — поверхня, sphere — сфера, cylinder— циліндр, ellipsoid — еліпсоїд, cone — конус, hyperboloid of one sheet — однопорожнинний гіперболоїд, hyperboloid of two sheets — двопорожнинний гіперболоїд.
85
Main tasks: 1. Construction of equations of straight lines and planes with different given elements. 2. Construction of equations of the second order curves and surfaces. 3. Studying of mutual location of straight lines and planes.
STUDENT MUST BE READY TO DO
THE FOLLOWING ASSIGNMENTS
1. Concepts, definitions, formulations:
•Different equations of a straight line (typical problems of finding equations of a straight line).
•Curves of the second order: a circle, an ellipse, a hyperbola, a parabola (their standard equations).*
•A plane. Different equations of a plane (typical problems on finding of equations of a plane).
•Cylindrical, conic surfaces.
•Surfaces of revolution.
•Method of sections.
2. Proofs and conclusions
•Different forms of the equation of a straight line on a plane (general, symmetric, parametric, passing through two points, in slope — intercept form, in «segments», normal).
•Mutual location of two straight lines. An angle between two straight lines. Conditions of parallelism and perpendicularity.
•Distance from a point to a straight line.
•Equation of a plane passing through a point perpendicularly to a given vector.
•Equation of a plane passing through three given points.
•Equation of a circle, an ellipse, a parabola.
•Symmetric equations of a straight line in space.
3. Assignments
•To work out the equation of a straight line passing through two points, through one point in the given direction.
•To work out equations of a plane passing through a point perpendicularly to a vector, through three points.
•To find angles between straight lines and planes.
•To find an intersection point of a straight line and a plane.
•To reduce equations of the second order to the standard form and to sketch their graphs.
86

Micromodule 7
BASIC THEORETICAL INFORMATION
STRAIGHT LINE ON A PLANE
General equation of a straight line, incomplete equations. Symmetric and parametric equations of a straight line. A straight line passing through two given points. An equation of a straight line in segments on axes, the slope — intercept form. An angle between two straight lines, conditions of parallelism and perpendicularity of two straight lines. Distance from a point to a straight line.
Literature: [1, chapter 6], [4, part 3, item 3.3], [6, chapter 3, § 3], [7, chapter 2, § 5], [9, chapter 2, § 2].
7.1. General equation of a straight line
Let us consider equations of a straight line L passing through the pointG Μ1 (x1 , y1 ) perpendicularly to the vector n = {Α, Β} (Fig. 2.1, a). The vector n
is called the normal vector of the straight line. Let us take an arbitrary point |
|||||||
Μ(x, y) |
on |
the line L and consider the vector |
JJJJJG |
y |
− y1} . It is |
||
Μ1Μ = {x − x1 , |
|||||||
obvious |
that |
|
JJJJJG |
perpendicular. According to |
|||
vectors nG = { Α, Β} and Μ1Μ are |
|||||||
|
|
|
|
|
|
G |
JJJJJJG |
condition of perpendicularity of two vectors their dot product is |
n |
Μ1Μ = 0 , |
|||||
that is, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Α(x − x1) + Β( y − y1) = 0. |
|
|
(2.1) |
|
|
|
|
|
|
|
|
|
The equation (2.1) is called the equation of a straight line passing through the point Μ1 (x1 , y1 ) perpendicularly to the normal n = { Α, Β} .
Removing brackets in the equation (2.1) and denoting − Αx1 − Βy1 = C we receive the equation of the straight line L
Αx + Βy + C = 0, |
(2.2) |
|
|
called a general equation of a straight line on a plane.
Let us consider special cases of location of a straight line depending on values of coefficients A, B, C (Table 7.1):
87
|
|
|
|
|
Table 7.1 |
|
|
|
|
|
|
||
Condition |
Equation |
Position of a straight line |
||||
of a straight line |
||||||
|
|
|
|
|||
|
|
|
|
|
||
А = 0, |
B ≠ 0 |
By + |
C = 0 |
It is parallel to the axis Ох |
||
|
|
|
|
|
||
В =0, |
A ≠ 0 |
Ах + |
C = 0 |
It is parallel to the axis Оу |
||
|
|
|
|
|
|
|
С = 0 |
|
Ах + Ву = 0 |
It passes through the origin of coor- |
|||
|
dinates |
|||||
|
|
|
|
|
||
|
|
|
|
|||
А = 0, С = 0, |
B ≠ 0 |
у = 0 |
It passes through the axis Ох |
|||
|
|
|
|
|||
В = 0, С = 0, |
A ≠ 0 |
х = 0 |
It passes through the axis Оу |
|||
|
|
|
|
|
|
|
|
|
|
7.2. Symmetric equation of a straight line |
||||||||||
Let a straight line L pass through the point |
Μ1 (x1 , |
y1 ) |
and be parallel to the |
||||||||||
vector aG = |
{ |
l, |
m called a direction vector of the straight line L (Fig. 2.1, b). We |
||||||||||
|
|
} |
|
|
|
|
|
|
|
|
|
|
|
take any point Μ(x, y) on the straight line L. |
|
|
|
|
|
|
|||||||
|
|
|
JJJJJJG |
} |
|
|
|
= {l, |
m} are collinear so |
||||
Then two vectors Μ1Μ = {x − x1 , y − y1 |
and a |
||||||||||||
their coordinates must be proportional: |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
x − x1 |
= |
y − y1 |
. |
|
|
(2.3) |
||
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
l |
m |
|
|
|
|
|
||
The equation (2.3) is called the symmetric equation of the straight line.
7.3. Equation of a straight line passing through two given points
Let a straight line L pass through two points |
Μ |
1 |
(x , y ) and |
Μ |
2 |
(x , |
y |
2 |
) |
||||||||||||
|
|
|
|
|
|
JJJJJJG |
|
|
|
1 |
1 |
|
2 |
|
|
||||||
(Fig. 2.1, c). Having chosen a vector |
Μ1Μ2 |
= {x2 − x1 ; |
y2 − y1} |
as a direction |
|||||||||||||||||
vector of the straight line L in the equation (2.3) we get the following equation: |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
x − x1 |
|
= |
y − y1 |
, |
|
|
|
|
|
|
|
(2.4) |
|||||||
|
|
x |
2 |
− x |
|
y |
2 |
− y |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
||
that is, an equation of a straight line passing through two given points.
88

|
y |
|
y |
a = l, m |
} |
|
nG |
= { Α, Β} |
|
||
L |
|
{ |
|||
M (x, y) |
|
|
M1(x1, y1) |
||
|
|
|
|||
|
|
|
|
M (x, y) |
|
|
O M1(x1, y1) |
x |
O |
|
x |
|
a |
|
|
b |
|
Fig. 2.1
y L
 M2(x2, y2)
M2(x2, y2)
 M1 (x1, y1) O x
M1 (x1, y1) O x
c
7.4. Parametric equations of a straight line
Let us take |
x − x1 |
= |
y − y1 |
|
= t . From here we get |
|||
l |
m |
|||||||
|
|
|
|
|||||
|
|
|
|
|
|
|||
|
|
|
|
x = x1 + lt, |
t R . |
|||
|
|
|
|
y = y + mt, |
||||
|
|
|
|
|
1 |
|
||
These equations of a straight line are called parametric.
7.5. Equation of a straight line in segments on axes
Let a straight line L pass through two points |
Α(a, |
0) |
and |
Β(0, b) , and cut |
||||||
off segments on coordinate axes whose lengths are | a | |
and |
| b | (Fig. 2.2, а). |
||||||||
Having substituted coordinates of points |
Α(a, 0) |
and |
Β(0, b) in the equation |
|||||||
(2.4) we get the equation |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
+ |
y |
= 1, |
|
|
|
|
(2.5) |
|
|
a |
b |
|
|
|
||||
|
|
|
|
|
|
|
|
|
||
called the equation of a straight line in segments on axes.
The general equation of a straight line (2.2) may be reduced to such form (2.5) only if all its coefficients are not zeros. Then
where − Αc = a, − Βc = b .
89
Remark. The straight line Αx + Βy + C = 0 in case A ≠ 0 , B ≠ 0 and C ≠ 0 crosses coordinate axes at points (−C / A; 0) and (0; −C / B) . To find coor-
dinates of these points it is enough to solve the equation (2.2) provided х= 0 and y = 0 in turn.
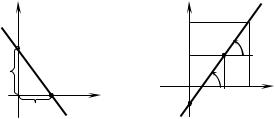
7.6. Equation of a straight line in slope–intercept form
If a straight line L passes through a point Μ0 (x0 , y0 ) and forms an angle α with the positive direction of the abscissa axis (Fig. 2.2, b) then the number
k = tg α is called a slope of the straight line. |
|
|
||||
Having taken any point Μ(x, y) |
on the straight line, we get from a triangle |
|||||
Μ0 ΜK |
|
|
|
|
y − y0 |
|
k = tg α = |
ΜK |
= |
, |
|||
|
x − x |
|||||
|
Μ |
0 |
K |
|
||
|
|
|
|
0 |
|
|
whence y − y0 = k (x − x0 ).
It is the equation of the straight line L passing through the point Μ0 (x0 , y0 )
and having the slope k. If we take a point B(0, b) |
as the point Μ0 we shall get |
||
the equation |
|
||
|
y = kx +b, |
|
(2.6) |
called the equation of a straight line in the slope — intercept form and b is the ordinate of the intersection point of the straight line with the axis Оу.
y
L
 B (0, b)
B (0, b)
│b│
О │a│ |
А(а, 0) |
x |
|
а |
|
y y
y0 |
M0 α |
|
|
|
α |
О |
x0 |
|
B(0,b) |
|
b |
Fig. 2.2
L
 M (x,y)
M (x,y)
K
x x
7.7. Angle between two straight lines.
Conditions of parallelism and perpendicularity of straight lines
For the given straight lines whose equations are y = k1 x + b1 and y = k2 x + b2 (Fig. 2.3) an acute angle between these straight lines is ϕ =|α2 − α1 | , therefore
90
