7. Оценка погрешностей измерений

1. Погрешности прямыхизмерений.

В данной лабораторной работе прямым способом измеряются две величины: координата груза x(начальная и конечная) и время падения грузаt.

Координата груза измеряется по линейке, закреплённой на стойке. Абсолютная погрешность измерения составляет половину деления шкалы, то есть 0,5 см, так что (x) = 0,5 см.

Время падения груза tизмеряется секундомером, который встроен в мобильный телефон. Класс точности этого секундомера зависит от модели телефона, но этот класс точности практически не влияет на погрешность измерения времени падения(t), так как основной вклад в(t) вноситслучайнаяпогрешность, вызванная несовершенством реакции человека. Для оценки случайной погрешности необходимо провести многократные измерения. Это значит, что один из семи опытов надо проделать не один раз, а несколько – не менее пяти. Рекомендуется выбрать для этого тот опыт, в котором высота падения максимальна (опыт № 1). Так как один раз этот опыт уже проведён, то его надо просто повторить ещё 4 раза. Иными словами, надо проделать ещё 4 раза пункты 4.4 – 4.6,не меняяпри этом высоту подъёма груза. Результаты опытов (вместе с тем, который уже проведён ранее) запишите в таблицу 5.1.

Таблица 5.1. Оценка случайной погрешности времени падения груза t

Номер опыта	t			(t)
	с	с	с2	с
1
2
3
4
5
Средние:

Поясненияк заполнению таблицы 5.1.

• Во втором столбце таблицы запишите пять результатов измерения времени падения – из-за неизбежной неточности действий экспериментатора все эти пять чисел не будут одинаковыми, хотя некоторые из них могут и совпасть.

• Вычислите среднее арифметическое значение времени падения и запишите результат внизу второго столбца (в строке «Средние»).

• В третьем столбце запишите отклонения tкаждого из значений времени падения от среднего значения. Одни из отклонений получатся положительными, другие – отрицательными.

• Вычислите среднее арифметическое значение отклонений и запишите внизу третьего столбца (в строке «Средние»). Должно получиться число, которое много меньше, чем(может быть, даже нуль). Это будет признаком правильности вычислений.

• В четвёртом столбце запишите квадраты отклонений , возводя в квадрат каждое из чиселtпредыдущего столбца.

• Определите дисперсию D(t) по формуле:

, (5.1)

где n– число опытов, которое в данном случае равно 5. Обратите внимание: дисперсия вычисляется почти так же, как и среднее арифметическое: надо сложить все числа, а потом поделить – но не на количество чиселn, а на (n– 1). Полученное значение дисперсии запишите внизу четвёртого столбца (в строке «Средние»).

• Определите стандартное отклонение (t) по формуле. Результат запишите в последнем (пятом) столбце таблицы.

Так как в основной серии опытов³все измерения –однократные, то погрешность измерения времени падения(t) для всех опытов основной серии равна стандартному отклонению(t).

Замечание. Стандартное отклонение можно определить, используя программу EXCEL – там для этого есть функция СТАНДОТКЛОН.В.

2. Погрешность измерения высоты подъёма груза (h). Высота подъёма измеряется косвенно, с использованием формулы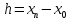, поэтому, в соответствии с правилами оценки погрешностей косвенных измерений,

.(5.2)

3. Погрешность измерения скорости падения груза 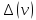. Скорость падения измеряетсякосвенно, с использованием формулы, поэтому относительная погрешность измерения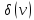равна:

. (5.3)

Абсолютная погрешность связана с относительной погрешностью формулой

. (5.4)

4. Погрешность измерения ускорения грузов a. Ускорение грузов измеряется косвенно, с использованием графика экспериментальной зависимостии формулы (2.7). В этом случае погрешность(a) можно оценить так.

• Проведите на графике зависимости две вспомогательные прямые линии (временно). Обе они должны пройти через планки погрешностей экспериментальных точек и через начало координат, но при этом первую из вспомогательных линий надо провести как можно круче, а вторую – как можно более полого.

• Измерьте описанным в пункте 4.11 методом два предельных значения ускорения, используя сначала первую вспомогательную прямую, затем – вторую. Это будет a_maxиa_min.

• Определите погрешность (a) по формуле:

. (5.4)

• Удалите с графика вспомогательные прямые линии.