
- •П.А. Киселев, с.Б. Бокуть курс лекций по физической химии
- •Введение
- •Лекция 1. Газовые законы
- •1.1. Температура и нулевой закон термодинамики
- •1.2. Законы поведения идеальных газов: уравнение состояния идеального газа
- •1.3. Кинетическое уравнение газов
- •1.4. Уравнение состояния реальных (неидеальных) газов. Уравнение Ван-дер-Ваальса
- •1.5. Закон парциальных давлений Дальтона
- •Лекция 2. Первое начало термодинамики и термохимия
- •2.1. Вводная часть
- •2.2. Некоторые понятия, используемые в термодинамике
- •2.3. Формулировка первого начала термодинамики
- •2.4. Применение первого начала термодинамики к различным процессам
- •2.5. Теплота химической реакции (общие положения)
- •2.6. Закон Гесса
- •2.7. Следствие из закона Гесса
- •Лекция 3. Второе начало термодинамики и его применение
- •3.1. Основной смысл и значение второго закона термодинамики
- •3.2. Обратимые и необратимые процессы
- •3.3. Формулировка и математическое выражение второго начала термодинамики
- •3.4. Изменение энтропии изолированной системы
- •3.5. Статистическая природа второго начала термодинамики
- •Лекция 4. Третье начало термодинамики. Расчеты изменения энтропии при различных процессах
- •4.1. Формулировка третьего начала термодинамики
- •4.2. Абсолютные и стандартные значения энтропии
- •4.3. Расчеты изменения энтропии в различных процессах
- •1. Расчеты изменения энтропии при изотермических процессах
- •2. Расчет изменения энтропии в неизотермических процессах
- •3. Расчет изменения энтропии сложного процесса
- •4.4. Расчет изменения энтропии при протекании химического процесса
- •4.5. Критерии направления протекания процессов и достижения равновесных состояний в открытых и закрытых системах. Понятие об энергии Гиббса
- •Лекция 5. Химические реакции как открытые в термодинамическом смысле системы. Направление протекания химических реакций. Равновесные химические реакции
- •5.1. Понятие о химическом потенциале
- •5.2. Экзергонические и эндергонические реакции
- •5.3. Взаимосвязь энтальпийного и энтропийного факторов в качестве критерия самопроизвольного протекания химической реакции
- •5.4. Понятие о равновесии химической реакции. Обратимые и необратимые реакции
- •5.5. Уравнение изотермы химической реакции и вывод закона действующих масс
- •5.6. Зависимость константы химического равновесия от температуры
- •Лекция 6. Химическое равновесие в гетерогенных и гомогенных системах
- •6.1. Взаимосвязь химического потенциала с другими термодинамическими функциями
- •6.2. Летучесть
- •6.3. Идеальный раствор
- •6.4. Фазовая диаграмма содержит зоны, линии и тройную точку
- •6.5. Уравнение Клаузиуса-Клапейрона
- •6.6. Коллигативные свойства растворов
- •6.7. Понижение точки замерзания и повышение точки кипения растворов
- •6.8. Осмотическое давление
- •6.9. Растворы электролитов
- •Лекция 7. Растворы электролитов
- •7.1. Общие сведения о теории электролитической диссоциации
- •7.2. Сильные и слабые электролиты
- •7.3. Закон разведения
- •7.4. Сильные электролиты
- •7.5. Ионная сила
- •7.6. Произведение растворимости
- •7.7. Электролитическая диссоциация воды
- •7.8. Концентрация водородных ионов
- •7.9. Буферные растворы
- •7.10. Механизм действия буферных растворов
- •7.11. Буферная емкость
- •Лекция 8. Основные понятия химической кинетики
- •8.1. Химическая реакция
- •8.2. Механизм химической реакции
- •8.3. Исходные, конечные и промежуточные вещества
- •8.4. Глубина превращения реакции
- •8.5. Гомогенные и гетерогенные реакции
- •8.6. Скорость химической реакции
- •8.7. Измерение скорости реакции
- •8.8. Порядок реакции и константа скорости реакции
- •8.9. Молекулярность реакции
- •8.10. Количественные соотношения между скоростью реакции и концентрацией реагента
- •8.11. Реакция второго порядка
- •8.12. Уравнение скорости реакции третьего порядка
- •8.13. Уравнение скорости реакции нулевого порядка
- •8.14. Определение порядка реакции
- •8.15. Теоретические основы химической кинетики
- •8.15.1. Теория активных соударений
- •8.15.2. Теория активированного (переходного) комплекса (переходного состояния)
- •8.15.3. Вывод основного уравнения теории переходного состояния
- •8.15.4. Термодинамическая форма основного уравнения теории переходного состояния
- •8.15.5. Сравнение термодинамической формы основного уравнения теории переходного состояния с уравнением Аррениуса
- •Лекция 9. Основы кинетики и механизма ферментативных реакций. Гомогенный и гетерогенный катализ
- •9.1. Понятие катализа
- •9.2. Основы теории гомогенного катализа
- •9.3. Основы теории гетерогенного катализа
- •9.4. Ферменты как биологические катализаторы
- •9.5. Кинетика реакций, катализируемых ферментами
- •9.6. Физический смысл величин Km и Vmax
- •9.7. Уравнение Михаэлиса-Ментен и ферментативные механизмы
- •9.8. Общее уравнение скорости
- •Лекция 10. Электрохимия
- •10.1. Введение в электрохимию
- •10.2. Термодинамика электрохимических систем
- •10.3. Электродный потенциал
- •10.4. Двойной электрический слой на границе между металлом и раствором электролита
- •10.5. Зависимость плотности заряда от концентрации электролита
- •Лекция 11.Электродные и безэлектродные электрохимические системы
- •11.1. Правила записи эдс и электродных потенциалов электрохимических систем
- •11.2. Типы электродов
- •11.3. Диффузионный и межжидкостный потенциалы
- •На электродах протекают реакции
- •11.5. Концентрационные цепи
- •Лекция 12. Поверхностные явления и адсорбция
- •12.1. Общая характеристика поверхностных явлений
- •12.2. Поверхностные явления в дисперсных системах
- •12.3. Поверхностное натяжение и природа вещества
- •12.4. Термодинамика поверхностных явлений в однокомпонентных системах
- •12.5. Равновесие фаз при искривленной поверхности раздела. Капиллярность
- •12.6. Уравнение Томсона
- •12.7. Капиллярные явления
- •Лекция 13. Адсорбция
- •13.1. Уравнение адсорбции Гиббса
- •13.2. Обзор сорбционных явлений
- •13.3. Природа адсорбционного взаимодействия
- •13.4. Термическое уравнение адсорбции. Изотерма адсорбции
- •13.5. Мономолекулярная адсорбция и изотерма Ленгмюра
- •Литература
- •Содержание
6.4. Фазовая диаграмма содержит зоны, линии и тройную точку
Для зоны с = 1, р = 1 иf= 2. Для линий с = 1,р = 2 иf= 1. Для тройной точки с = 1,р = 3 иf= 0. Что означают различные степени свободы? То, что внутри зонf = 2, означает следующее: для описания поведения системы мы должны использовать и температуру и давление, т.е. обе величины могут меняться без изменения числа фаз, значит вода существует в жидком состоянии при различных температурах и давлениях.f= 1 означает, что мы можем установить точку на линии, т.е. описать систему только температурой или давлением. Т.е. вдоль линии каждой температуре соответствует строго определенное давление пара. При любом давлении пара для льда существует только одна точка для температуры плавления. В тройной точке система инвариантна, т.е.f= 0, т.е. система может находиться в равновесии только при одном значении температуры и давления.
6.5. Уравнение Клаузиуса-Клапейрона
Из рис. 6.1 видно, что наклон ВО и ОА на графике задается производной dp/dT, которая представляет собой скорость изменения давления пара отТ. Наклон ОС численно равенdp/dT– величина, обратная скорости, с которой точка плавления изменяется при изменении давления. Уравнение, которое связывает эти изменения с другими измеряемыми свойствами системы, было предложено в 1834 году Б. Клапейроном и позже модифицировано Р. Клаузиусом.
Это уравнение можно вывести, используя термодинамические соотношения для химического потенциала. В принципе любые свойства (такие, как объем, энтальпия, свободная энергия) зависят от количества вещества и являются экстенсивными. Однако если они относятся к одному молю вещества в строго определенных условиях, они становятся характеристичными свойствами вещества при данных условиях.
Объем, реально занимаемый одним молем растворенного вещества, называется парциальным молярным объемом растворенного вещества. Он соответствует изменению общего объема очень большого количества раствора при добавлении одного моля растворенного вещества. Очевидно, что при добавлении одного моля растворенного вещества концентрация не будет меняться только при условии бесконечно большого объема исходного раствора.
В этом случае для парциального объема можно записать:
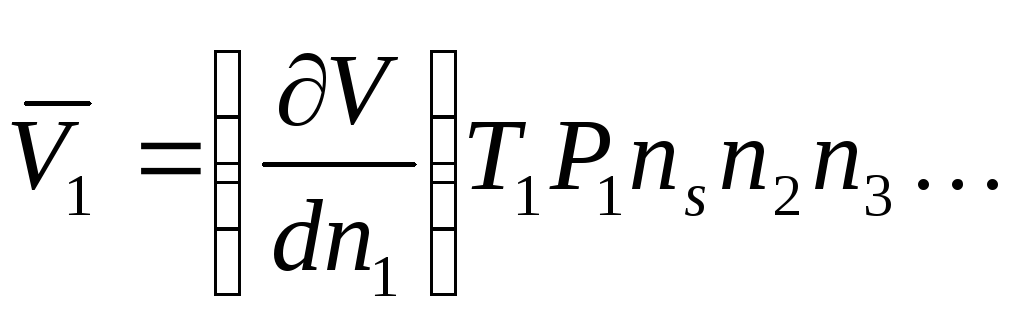 ,
,
где V– общий объем раствора,Т– температура,Р–давление,n – число молей других веществ. ВеличинаVявляется функциейТиР, а также состава раствора.
Если компонент распределен между двумя фазами и, то при равновесии. В случае однокомпонентной системы химический потенциал равен величине свободной энергии, приходящейся на 1 моль: =G и = G.
Если
будет слегка меняться при небольших
измененияхТ иР, то аналогичное
изменение будет наблюдаться и для(при сохранении равновесия). Поэтому
можно записать![]() .
.
Далее мы знаем, что
dG=Vdp-SdT. (6.4.)
Подставим в это уравнение выражение для парциальных молярных величин
![]() dp-SdT=Vdp-SdT.
(6.5)
dp-SdT=Vdp-SdT.
(6.5)
Преобразуем выражение (6.5) в виде члена dp/dT
![]() .(6.6)
.(6.6)
Выражение Sпо второму началу термодинамики![]() ,
гдеQобрпредставляет
собой молярную теплоту испарения или
молярную теплоту плавления.
,
гдеQобрпредставляет
собой молярную теплоту испарения или
молярную теплоту плавления.
Подставим Sв уравнение (6.6) и получим уравнение Клапейрона:
![]() .(6.7)
.(6.7)
В таком виде это
уравнение нельзя проинтегрировать.
Р. Клаузиус предложил несколько
допущений, что позволяет преобразовывать
уравнение в более удобную форму –
например, в случае равновесия
пар – вода
![]() равно (
равно (![]() ).
ВеличинаVждля воды составляет приблизительно
0,1% отVги поэтомуVжможно не учитывать в членеV(г)
– V(ж).
Тогда придем к уравнению
).
ВеличинаVждля воды составляет приблизительно
0,1% отVги поэтомуVжможно не учитывать в членеV(г)
– V(ж).
Тогда придем к уравнению
![]() .(6.8)
.(6.8)
Если
принять, что пар подчиняется законам
идеального газа, то вместо
![]() запишемRT /P:
запишемRT /P:
![]() .
.
Заменим выражение для Qболее традиционнымНV, получим уравнение Клаузиуса-Клапейрона в обычной форме:
![]() .(6.9)
.(6.9)
Это уравнение можно проинтегрировать, если предположить, что молярная теплота испарения НVявляется постоянной, т.е. не зависит от температуры. После интегрирования в пределах междуР1, Т1иР2, Т2получаем:

или в форме
![]() .(6.10)
.(6.10)
