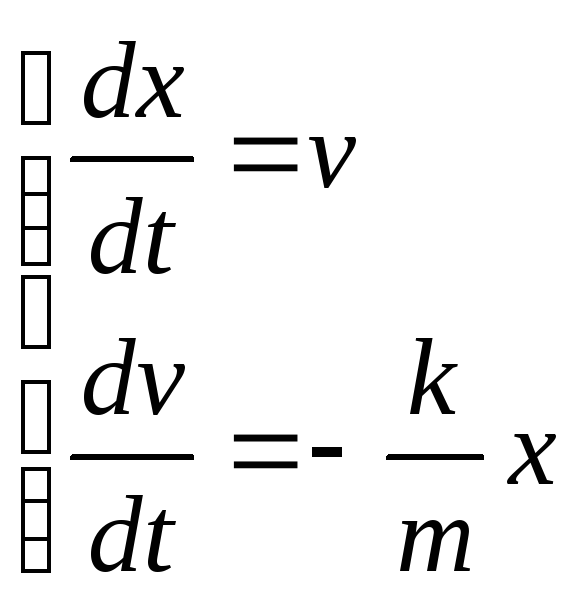8. Двумерные задачи с оду 2-го порядка

Следующим этапом является рассмотрение двумерных задач динамики. Типичным представителем этого класса является баллистическая задача

Баллистическая задача без учёта сопротивления среды

Рассмотрим тело, брошенное под углом к горизонту. В первом приближении можно пренебречь. Тогда на тело действует только сила тяжести. Уравнение динамики записывается в виде

и может быть расписано вдоль горизонтальной и вертикальной осей

,(18)

Как видно из уравнений, движение вдоль разных осей никак не связано друг с другом и может быть описано по отдельности, а для решения задачи можно воспользоваться уже имеющимися у нас алгоритмами.

Так как вдоль горизонтальной оси не действует никакая сила, проекция скорости на эту ось остаётся постоянной. . Вдоль вертикальной оси движение является равноускоренным с начальной скоростью. Следовательно, скорость обнулится за время. За это же время тело достигнет верхней точки траектории. Приведём пример расчёта траектории для тела, брошенного под углом 45 градусов к горизонту.

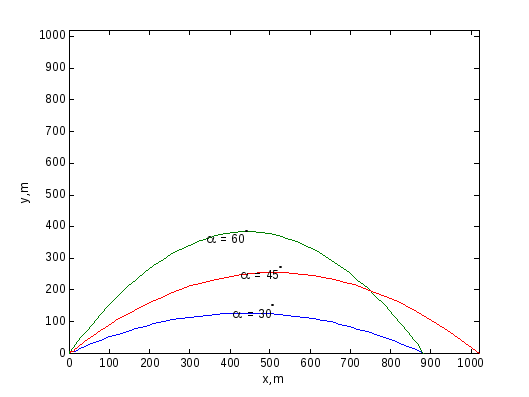
Рис. 8. Траектории тел, вылетевших под различными углами с начальной скоростью 100 м/с (без учёта сопротивления воздуха)

g=9.8;

alpha = 45*pi/180; V0=100;

Vx=V0*cos(alpha); Vy=V0*sin(alpha);

T=Vy/g;

[t1,y1]=ode45(@fall,[0 2*T],[0 Vy],[],g);

x1=Vx*t1;

plot(,x1,y1(:,1));

xlabel('x,m');ylabel('y,m');

axis([0 Vx*T 0 g*T*T]);

text(x1(30)y1(30.1),'\alpha = 45^{\circ}')

Баллистическая задача cучётом сопротивления среды

Как было показано в предыдущем разделе, турбулентное трение является основной силой, влияющей на движение тела в атмосфере. Оно описывается формулой (16). Уравнение динамики записывается в виде

Для проекций на оси получим

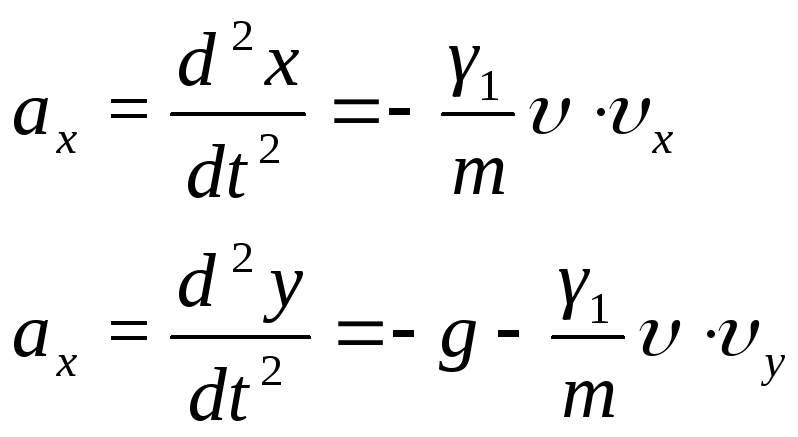(19)

где модуль скорости

Как видим из (19), в результате турбулентного трения движение по разным координатам уже нельзя рассматривать независимо, уравнения оказываются связанными т.к. скорость и модуль скорости зависит от обеих компонент. Совершив замену

,,,.

мы получим четырехкомпонентый вектор, для которого уравнения (19) запишутся в виде

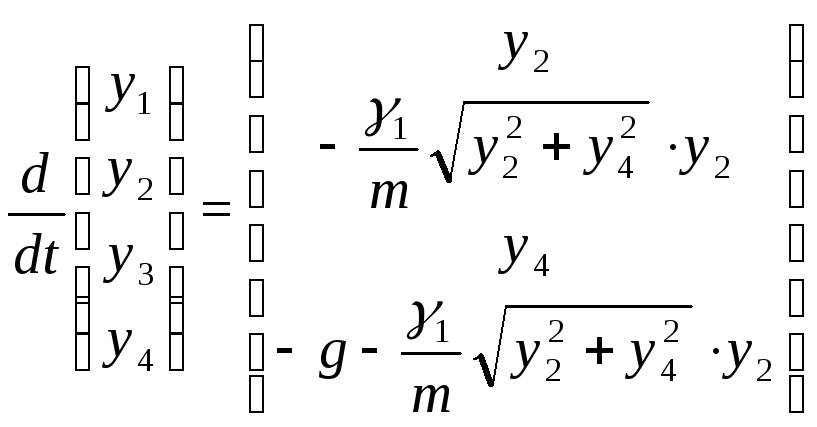
9. Алгоритм

Создаем функцию в отдельном М-файле

function dy = ballist(t,y,g,gamma)

V=sqrt(y(2)*y(2)+y(4)*y(4)));

dy=[y(2); - gamma*v*y(2);y(4);-g-gamma*v*y(4)];

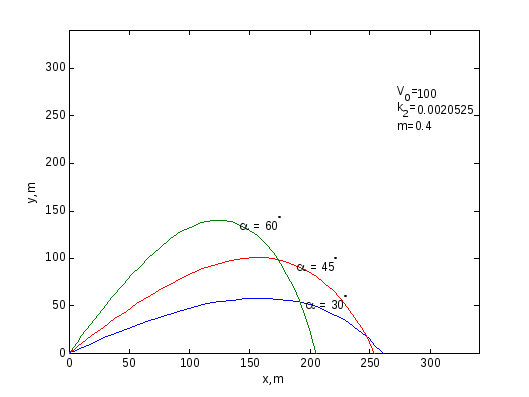
Рис. 9. Траектории тел, вылетевших под различными углами с начальной скоростью 100 м/с с учётом сопротивления воздуха

Произведём расчёт, используя эту функцию.

g=9.8; eta=1.86e-5; ro=7800; R=5e-2;

gamma=9*eta/(2*ro*R*R);

Vo=100; alpha=30*pi/180;

xmax=Vx*T/3; ymax=g*T*T/2/3;

[t,y]=ode45(@ballist,[0,T],[0 Vx 0 Vy],[],9.8,1e-3]);

plot(y(:,1),y(:,3)); xlabel(‘x,m’), ylabel(‘y,m’)

axis([0 Vx*T/3 0 g*T*T/2/3]);

text(xmax*0.8,ymax*0.8,'V_0='), text(xmax*0.85,ymax*0.8,V_0)

text(xmax*0.8,ymax*0.75,'k_2='), text(xmax*0.85,ymax*0.75,K)

В результате действия турбулентого трения траектории тела брошенного под углом 30^0- и 60⁰уже не совпадает - по настильной траектории тело летит дальше. Это связано с большим временем движения при броске навесом, в результате сила трения успевает совершить большую работу.

10. Колебания Механический (пружинный) маятник

Из второго закона Ньютона и закона Гука нетрудно получить уравнение динамики для маятника

,

которое легко преобразуется в уравнение свободных колебаний

,

где - квадрат циклической частоты собственных колебаний.

Математическая постановка задачи сводится к замене переменных, в результате которой мы из ОДУ второго порядка получаем систему ОДУ первого порядка