Задача 3. Нелинейная модель динамики численности популяции

Ещё один фактор, который необходимо учитывать в популяционной динамике, состоит в наличии пола. В таком случае прирост популяции определяется вероятностью встреч особей противоположного пола и поэтому пропорционален квадрату численности популяции (при равенстве долей обоих полов в ней): . Количество смертей, между тем, пропорционально численности популяции:. В результате получим уравнение

(11)

Как видим, уравнение подобно модели Мальтуса с показателем. Его значение зависит от численности популяции, соответственно, возможно три поведения системы:

1. – происходит убыль численности;

2. – состояние не меняется;

3. – идёт быстрый рост популяции.

3. Алгоритм

Создадим отдельный файл model_nl.m, описывающий функцию для решения дифференциального уравнения

function dn = model _nl(t,n,alpha,beta)

dn = alpha* n.* n – beta * n;

4. Модели на основе систем обыкновенных дифференциальных уравнений Задача 1. Популяционная задача с учетом полового состава

Динамика численности популяции с учётом полового состава определяется двумя уравнениями типа (11), образующими систему

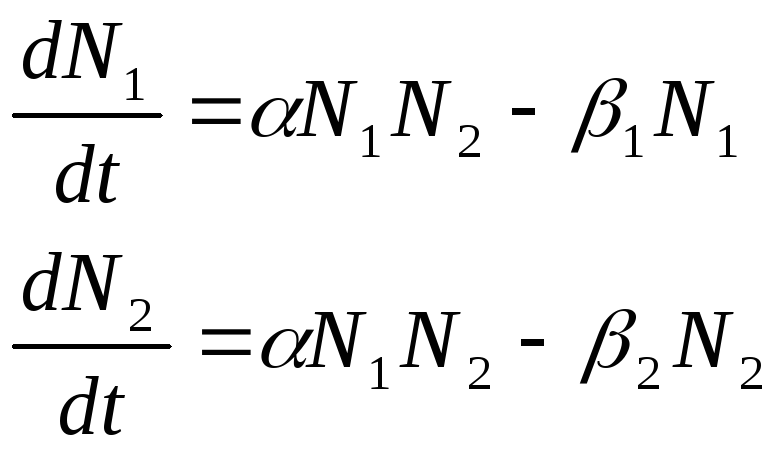(12)

5. Алгоритм

Создадим отдельный М-файл, где зададим функцию, описывающую ОДУ

function dy=popul(t,y,alpha,beta);

dy=[alpha*y(1)*y(2)-beta*y(1);

alpha*y(1)*y(2)-beta*y(2)];

Получим решение при помощи оператора решателя ОДУ по схеме Рунге-Кутты 4-5 порядков¹для различных начальных значений численности особей одного пола.

[t,y]=ode45(@popul, [0 20], [100 100],[],0.001,0.1);

[t1,y1]=ode45(@popul, [0 20], [110 100],[],0.001,0.1);

[t0,y0]=ode45(@popul, [0 20], [90 100],[],0.001,0.1);

Графически представим результаты расчетов, разбив графическое окно на два подокна: сверху – зависимость от времени численности особей одного поля, снизу – другого. Подпишем оси, нанесём сетку, в заголовок выпишем значения параметров.

subplot(211), plot(t,y(:,1),t1,y1(:,1),’--‘,t0,y0(:,1),’-.’), grid, xlabel('t'), ylabel('n_1')

title('dn_1/dt=\alphan_1\cdotn_2-\betan_1;\alpha=0.001; \beta=0.1; n_{10}=100; 110; 90; n_{20}=100')

subplot(212), plot(t,y(:,2),t1,y1(:,2),’--‘,t0,y0(:,2),’-.’), grid, xlabel('t'), ylabel('n_2'), title('dn_2/dt=\alphan_1\cdotn_2-\betan_2'), legend(‘n_{10}=100’, ‘n_{10}=110’, ‘n_{10}=90’)

Как видим, при наблюдается рост популяции, при- уменьшение её численности.

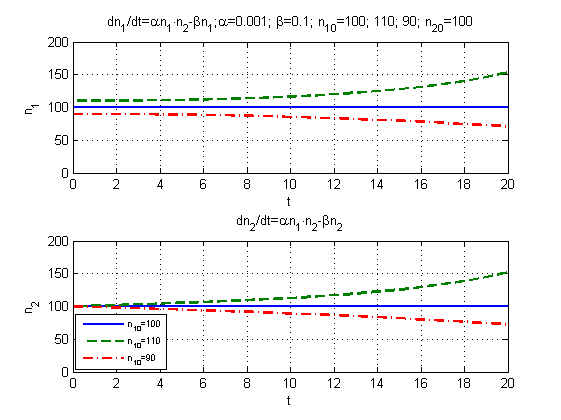
Рис. 5. Зависимости численности особей различных полов от времени в зависимости от начальных условий

6. Математические модели на основе обыкновенных дифференциальных уравнений 2-ого порядка. Задача 1: Свободное падение тела

Рассмотрим свободно падающее тело. На него действует лишь сила тяжести. Тогда второй закон Ньютона записывается ,

откуда

.

Для преобразования дифференциального уравнения второго порядка в систему дифференциальных уравнений первого порядка сделаем замену:

,.

Тогда получим

(13)

Алгоритм

Создадим отдельный М-файл, где зададим функцию, описывающую ОДУ

function dy=fall(t,y,g)

dy=[y(2); -g];

Получим решение при помощи оператора решателя ОДУ по схеме Рунге-Кутты 4-5 порядков (для различных значений ускорения свободного падения: на Земле, на Юпитере и на Луне) для тела, падающего с высоты 100 м без начальной скорости в интервале времени от 0 до 15 секунд.

[t,y]=ode45(@fall, [0 15], [100 0],[],9.8);

[t1,y1]=ode45(@fall, [0 15], [100 0],[],24.9);

[t0,y0]=ode45(@fall, [0 15], [100 0],[],1.62);

Графически представим результаты расчетов, разбив графическое окно на два подокна: слева – зависимость координаты от времени, справа – скорости. Обратите внимание на оператор axis, не позволяющий отображать результаты, лежащие ниже нулевого уровня.

subplot(121), plot(t,y(:,1),t1,y1(:,1),’--',t0,y0(:,1),’:’),

grid, xlabel('t'), ylabel('z'), title(‘dz/dt=V_z’)

axis([0 15 0 100])

legend('g=9.8m/s^2’; 'g=24.9 m/s^2’, 'g=1.62 m/s^2’)

subplot(122), plot(t,y(:,2),t1,y1(:,2),’--',t0,y0(:,2),’:’),

grid, xlabel('t'), ylabel('V_z'), title(‘dV_z/dt=-g’)

Результаты представлены на рисунке 6. Как и ожидалось, зависимость высоты от времени представляет собой отрезок параболы, а график скорости – линейную зависимость. Скорость нарастает тем быстрее, чем больше ускорение свободного падения. Проверив себя на данном примере, можем перейти к более сложным задачам.

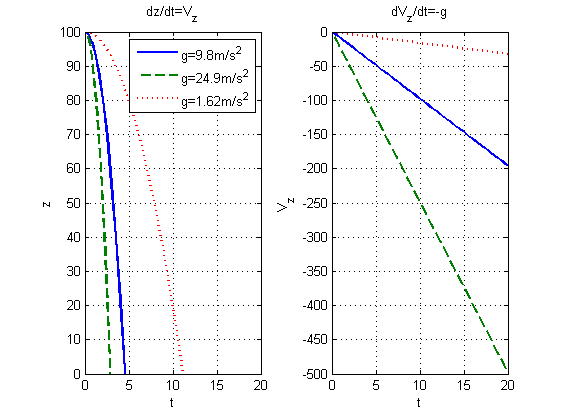
Рис. 6. Зависимости высоты и скорости тела от времени при свободном падении