18. Падение тела с большой высоты

    1. Задание

1. Смоделируйте падение тела на поверхность Земли с высоты 1000 км, учитывая изменение ускорения свободного падения с расстоянием до Земли. Сопротивлением атмосферы пренебречь, падение считать строго вертикальным. За какое время тело упадет на Землю? Какой скоростью оно будет обладать в конце пути? Будет ли результат расчета зависеть от массы тела?

2. Произведите аналогичный расчет для высоты 100 км и 10 000 км. Во сколько раз изменилось время падения и конечная скорость?

3. Введите в модель турбулентное трение атмосферы. При этом необходимо учесть изменение плотности атмосферы с высотой (считать, что оно подчиняется распределению Больцмана). Произведите расчет для железного метеора (плотность 7800 кг/м³) в форме шара диаметром 1 мм, упавшего с высоты 100 000 км. Коэффициент трения принять равным 10^-3.

4. Какая часть кинетической энергии метеора перейдет в тепло? Считая, что половина этой энергии ушла на нагрев метеора, рассчитать его температуру. Теплоемкость железа приведена в таблице, по ней построить аппроксимацию полиномом.

Т,К	20	40	80	150	250	400	600	1000	1500
с, Дж/(кг·К)	4.6	30	138	324	422	489	574	975	654

Температура плавления железа 1538 С, кипения 2872 С. Теплота плавления 13.8 кДж/моль, испарения – 350 кДж/моль, молярная масса 56 г/моль.

5. Произведите расчет температуры для метеоров диаметром 10, 100 мкм и 10 мм, считая, что коэффициент трения пропорционален квадрату радиуса. Долетит ли какой-нибудь из них до поверхности Земли?

19. 3.2. Краткое Содержание лекций

    1. Математическое моделирование

Математическое моделирование позволяет глубже понять физический процесс, а также рассмотреть условия, которые преимущественно не могут быть достигнуты в эксперименте.

Этапы построения модели:

1. Создаётся физическая модель – осуществляется выбор закона, описывающего явление, оцениваются значения параметров задачи и т. д.

2. Создаётся математическая модель – производится запись уравнений, которые затем требуется решить.

3. Осуществляется выбор алгоритма для решения математической модели.

4. Производится подгонка параметров модели и проверка её адекватности.

Характерной особенностью является наличие общих математических моделей для многих процессов. Таким образом, разработав алгоритм решения одной задачи, мы можем получить возможность к решению целого спектра задач.

Пример 1.Радиоактивный распад описывается дифференциальным уравнением

(1)

где - константа распада,N - количество радиоактивных ядер. Решением этого уравнения является выражение

, (2)

из которого видно, что время релаксации - время, за которое количество ядер уменьшается вeраз. Оно связано с периодом полураспадаTформулой, которую можно получить из соотношения

Пример 2.Процесс теплопроводности от тела с температуройT в окружающую среду с температуройчерез материал с теплопроводностьюописывается уравнением

. (3)

Как и в предыдущей задаче, разность температур спадает по экспоненте

. (4)

Пример 3. Как известно, при движении в вязкой среде возникает вязкое трение. Уравнение движения записывается в данном случае в виде, аналогичном (1)

, (5)

где – коэффициент, зависящий от вязкости среды, формы тела и его массы.

Соответственно, скорость тела в вязкой среде должна спадать по экспоненте: , где- время релаксации. Заметим, что такая зависимость наблюдается только при ламинарном обтекании тела, при возникновении турбулентных вихрей сила сопротивления становится пропорциональна квадрату скорости

Пример 4.Диффузия также описывается дифференциальным уравнением, аналогичным (3). Рассмотрим процесс диффузии с поверхности

. (6)

Здесь N- количество молекул, продиффундировавших через площадкуSза счёт градиента концентрации,- коэффициент диффузии,– характерный масштаб изменения концентрации вещества. В результате диффузии разность концентраций будет спадать по экспоненте.

где - время релаксации.

Пример 5. Разрядка конденсатора с зарядоми ёмкостьючерез резистор с сопротивлениемописывается аналогичным уравнением. Действительно, согласно 2-му правилу Кирхгофа напряжение в такой схеме складывается из напряжений на конденсаторе и на резисторе

Отсюда получим дифференциальное уравнение

. (7)

с решением

.

Пример 6. Спад тока, протекающего через индуктивностьс сопротивлением, описывается уравнением того же типа. ЭДС самоиндукции в катушке компенсируется падением напряжения на сопротивлении:, откуда получаеми

. (8)

Решение, как и в предыдущих случаях – экспонента.

Пример 7.Кинетика химических реакций типаописывается теми же уравнениями: изменение концентрации вещества А прямо пропорционально произведению концентраций обоих веществ.

(9)

Отличие состоит в том, что время релаксации здесь определяется концентрацией второго вещества .

Пример 8.Аналогичные модели используются в популяционных задачах. Рассмотрим модель Мальтуса. Численность популяцииза времяизменяется благодаря рождаемостии смертности. При сложении этих изменений получим дифференциальное уравнение первого порядка

(9)

с решением . В случае, если рождаемость превышает смертность, получаем экспоненциальный рост численности, в обратном случае - спад. При равенстве этих показателей численность не меняется.

Проведём моделирование этой задачи в среде MATLAB. В отдельном файлеmaltus.mзададим функцию, описывающую дифференциальное уравнение

function dn = maltus (t,n,alpha,beta)

dn = (alpha-beta)*n;

Теперь зададим коэффициенты и используем эту функцию в операторе решения обыкновенных дифференциальных уравнений по схеме Рунге-Кутта 2-3 порядка

alpha = 0.01; beta = 0.02;

[t,n]=ode23(@maltus,[0 20],100,[],alpha,beta);

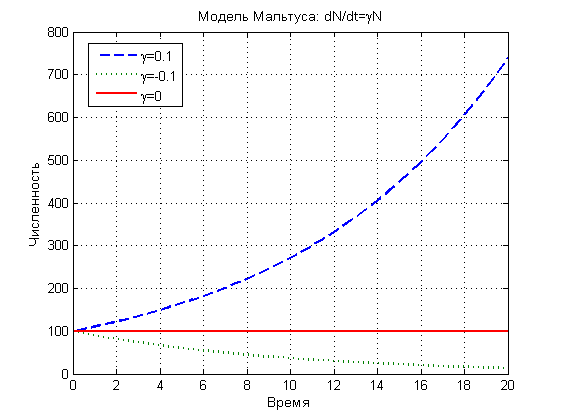
Рис. 1. Зависимости численности популяции от времени в модели Мальтуса

Результат отобразим в виде графика, подписав оси и дав заголовок графику.

plot(t,n)

xlabel(‘Время ‘)

ylabel(‘Численность’)

title(‘Модель Мальтуса: dN/dt=\gammaN’).

На рисунке 1 показаны результаты расчёта для трёх ситуаций: ,,. Как видно из него, за 10 лет численность популяции меняется вeраз.