
- •Введение
- •Основные понятия и аксиомы статики
- •1.1 Сила и система сил
- •1.3. Аксиомы статики
- •Связи и их реакции
- •4. Связь с неподвижным центром вращения (сферический шарнир)
- •5. Опорный стержень
- •3. Система сходящихся сил
- •3.1 Теорема о равновесии тела под действием сходящейся системы сил(векторные условия равновесия)
- •Аналитические условия равновесия тела, загруженного сходящейся системой сил
- •Теорема о трех непараллельных силах (правило трех сил)
- •4. Момент силы
- •4.1. Момент силы относительно оси
- •4.2. Момент силы относительно полюса (центра, точки)
- •4.3. Момент силы относительно полюса как векторное произведение
- •4.4 Связь между моментами силы относительно полюса и оси
- •4.5. Главный момент системы сил
- •4.6. Зависимость между главными моментами системы сил относительно двух полюсов
- •4.7. Теорема Вариньона (частный случай)
- •Элементарные операции статики. Эквивалентные системы сил
- •Элементарные операции статики
- •5.2. Эквивалентные преобразования. Эквивалентные системы сил. Равнодействующая
- •5.3. Обобщенная теорема Вариньона
- •6. Условия равновесия. Условия равновесия в общем и частных случаях
- •6.1. Основная лемма статики
- •6.2. Основная теорема статики (общие условия равновесия системы сил)
- •6.3. Аналитические условия равновесия произвольной системы сил (шесть уравнений статики абсолютно твердого тела)
- •6.4 Частные случаи аналитических условий равновесия
- •7. Общий признак эквивалентности двух систем сил (критерий эквивалентности)
- •8. Теория пар сил
- •8.1. Момент пары сил
- •8.2. Признак эквивалентности двух пар сил
- •8.3. Следствия из признака эквивалентности пар
- •8.4. Теорема о "сложении" пар
- •9. Приведение системы сил к заданному центру
- •9.1. Лемма о параллельном переносе силы
- •9.2. Теорема Пуансо (о приведении системы сил к заданному центру)
- •9.3. Частные случаи приведения системы сил к заданному центру
- •9.4. Инварианты системы сил
- •10. Центр параллельных сил. Центр тяжести
- •10.1. Центр системы параллельных сил
- •10.2. Центр тяжести твердого тела
- •2. Центр тяжести плоской фигуры
- •3. Центр тяжести линии
- •10.3. Статические моменты
- •10.4. Центры тяжести симметричных тел
- •10.5. Основные способы определения центра тяжести
- •11. Трение скольжения
- •11.1. Сила трения и коэффициент трения
- •11.2. Угол трения. Конус трения
9.2. Теорема Пуансо (о приведении системы сил к заданному центру)
Теорема.Любая система сил эквивалентна системе, состоящей из силы и пары сил. Сила приложена в любой наперед заданной точке (центре приведения) и геометрически равна главному вектору системы сил. Момент пары равен главному моменту исходной системы сил относительно центра приведения.
Доказательство.
 Пусть
точка
Пусть
точка![]() – центр приведения (полюс приведения).
Приведем исходную систему сил
– центр приведения (полюс приведения).
Приведем исходную систему сил![]() к центру
к центру![]() ,
пользуясь леммой о параллельном переносе
силы.
,
пользуясь леммой о параллельном переносе
силы.
Вначале
приведем силу
![]() к заданному центру (рис. 41), которая будет
эквивалентна силе
к заданному центру (рис. 41), которая будет
эквивалентна силе![]() и паре
и паре![]() :
:
![]() ,
, ![]() .
.
 Аналогично
поступим с остальными силами исходной
системы
Аналогично
поступим с остальными силами исходной
системы![]() (рис. 42).
(рис. 42).
Получим,
что система
![]() ~
~
![]() и парам
и парам![]() ,
,![]() ,…,
,…,![]() .
Силы
.
Силы
![]() приложены в точке
приложены в точке ![]() (сходящиеся силы) и могут быть заменены
одной силой, приложенной в точке
(сходящиеся силы) и могут быть заменены
одной силой, приложенной в точке![]() и геометрически равной главному вектору
и геометрически равной главному вектору
![]() .
.
Система
пар
![]() ,
,![]() ,…,
,…,![]() по теореме о "сложении" пар
эквивалентна одной паре
по теореме о "сложении" пар
эквивалентна одной паре![]() ,
момент которой равен сумме моментов
всех пар системы, которая в свою очередь
равна главному моменту исходной системы
сил относительно центра приведения
,
момент которой равен сумме моментов
всех пар системы, которая в свою очередь
равна главному моменту исходной системы
сил относительно центра приведения
![]()
![]() .
.
Теорема доказана.
9.3. Частные случаи приведения системы сил к заданному центру
Пусть
в результате приведения системы сил к
заданному центру
![]() получилось:
получилось:
 ,
,
 — система находится в равновесии; можно
сказать, что она приводится кпрямо
противоположным силам.
— система находится в равновесии; можно
сказать, что она приводится кпрямо
противоположным силам.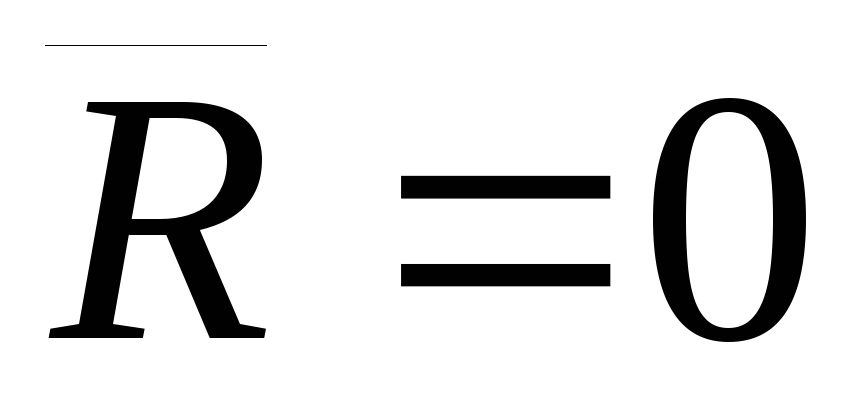 ,
,
 — сила отсутствует, система приводится
кпаре сил.Выбор полюса приведения
не влияет на момент пары сил.
— сила отсутствует, система приводится
кпаре сил.Выбор полюса приведения
не влияет на момент пары сил. ,
,
 — система приводится к одной силе –равнодействующей.
— система приводится к одной силе –равнодействующей.
 ,
,
 ,
,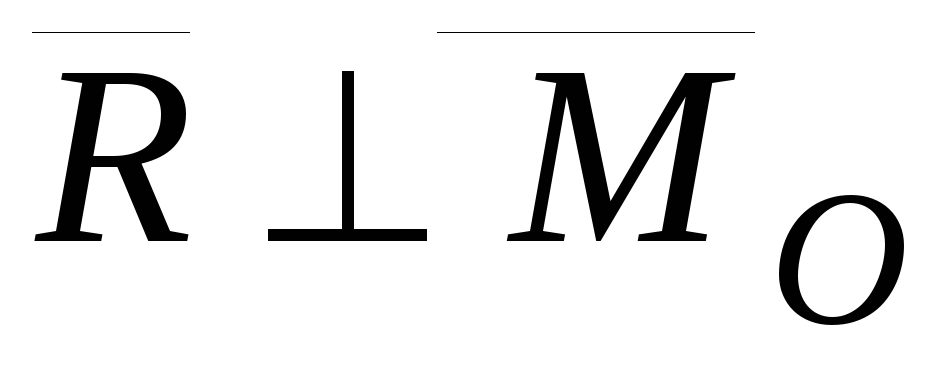
Через точку
![]() проведем плоскость, перпендикулярную
вектору момента
проведем плоскость, перпендикулярную
вектору момента![]() (рис. 43). Приведем систему сил к силе
(рис. 43). Приведем систему сил к силе![]() и паре сил
и паре сил![]() ,
,![]() – центр приведения. Сила
– центр приведения. Сила![]() лежит в проведенной плоскости, приложена
в центре приведения
лежит в проведенной плоскости, приложена
в центре приведения![]() и равна главному вектору:
и равна главному вектору:![]() .
Пара сил
.
Пара сил![]()
с
моментом
![]() также лежит в проведенной плоскости.
Одну из сил пары выберем равной и прямо
противоположной силе
также лежит в проведенной плоскости.
Одну из сил пары выберем равной и прямо
противоположной силе![]() :
:![]() .
Другую силу пары
.
Другую силу пары![]() (
(![]() )
проводим так, чтобы момент пары был
равен главному моменту системы сил, то
есть
)
проводим так, чтобы момент пары был
равен главному моменту системы сил, то
есть![]() .
.
Полученная
система сил
![]() эквивалентна одной силе
эквивалентна одной силе![]() ,
так как применяя элементарную операцию,
прямо противоположные силы
,
так как применяя элементарную операцию,
прямо противоположные силы![]() и
и![]() можно отбросить. Система сил приводится
к равнодействующей.
можно отбросить. Система сил приводится
к равнодействующей.
Общий признак существования равнодействующей
Объединяя частные случаи 2 и 4 можно установить общий признак существования равнодействующей.
Система сил приводится к равнодействующей, если главный вектор не равен нулю, а скалярное произведение главного вектора на главный момент равно нулю:
![]() ,
, ![]() .
.
Действительно,
![]() (при
(при![]() ),
если
),
если![]() или
или![]() ,
то есть
,
то есть![]() .
.
 ,
,
 ,
, //
// .
.
П лоскость
пары перпендикулярна векторам силы
лоскость
пары перпендикулярна векторам силы![]() и момента
и момента![]() .
Таким образом, система эквивалентна
силе
.
Таким образом, система эквивалентна
силе![]() и паре
и паре![]() ,
плоскость которой перпендикулярна силе
(рис. 44)
,
плоскость которой перпендикулярна силе
(рис. 44)
Определение. Совокупность силы и пары сил, которая лежит в плоскости, перпендикулярной этой силе называют динамическим винтом или динамой.
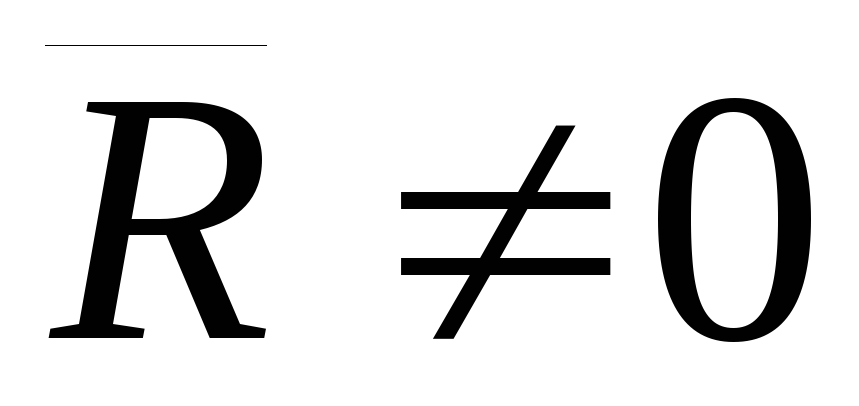
 ,
,
 ,
, (рис. 45а).
(рис. 45а).
Разложим
вектор момента
![]() на две составляющие:
на две составляющие:![]() //
//![]() ,
,![]() (рис 45б). Через точку
(рис 45б). Через точку![]() проведем плоскость, перпендикулярную
вектору
проведем плоскость, перпендикулярную
вектору![]() и построим пару
и построим пару
![]() такую, что
такую, что![]() ,
,![]() ,
а момент пары
,
а момент пары![]() (рис. 45в). Таким образом, сила
(рис. 45в). Таким образом, сила![]() и пара сил с моментом
и пара сил с моментом![]() эквивалентны силе
эквивалентны силе![]() ,
приложенной в точек
,
приложенной в точек![]() ,
на расстоянии:
,
на расстоянии:
![]() .
.
Следовательно,
исходная система сил эквивалентна силе
![]() и паре сил с моментом
и паре сил с моментом![]() ,
причем векторы
,
причем векторы![]() и
и![]() параллельны. Система приводится к
динаме.
параллельны. Система приводится к
динаме.
Общий признак приведения системы сил к динаме
Объединяя случаи 5 и 6, получим:
Система сил эквивалентна динаме, если скалярное произведение её главного вектора на главный момент не равно нулю:
![]() .
.
Теорема Пуансо и частные случаи из нее позволяют привести заданную систему сил к простейшему виду.
Простейшие виды системы сил Условия приведения
1.
Прямопротивоположные силы ![]() .
.
2.
Пара сил ![]() .
.
3.
Одна сила (равнодействующая) ![]() .
.
4.
Динама ![]() .
.
