7. Общий признак эквивалентности двух систем сил (критерий эквивалентности)

Теорема.Для того, чтобы две системы силбыли эквивалентны, необходимо и достаточно, чтобы у этих систем были геометрически равны соответственно главные векторы и главные моменты относительно одного и того же полюса.

Доказательство.

Необходимость.

Дано: .

Следует доказать, что у этих систем сил равны главные векторы и главные моменты относительно одного и того же полюса, то есть что

, .

Доказательство: Системы сил иэквивалентны, следовательно, одна из другой могут быть получены с помощью элементарных операций. Но элементарные операции не изменяют главный вектор и главный момент системы сил – второе (геометрическое) свойство элементарных операций, поэтому,.

Достаточность.

Дано: две системы сил и, главные векторы и главные моменты которых равны, то есть,.

Доказать, что системы иэквивалентны.

Доказательство: Не ограничиваясь в общности, проводим доказательство в предположении, что каждая из системисостоит из двух сил, то есть пусть даны системы сили(рис 34а). В силу основной леммы статики системы сили, содержащие произвольное число сил всегда при помощи элементарных операций могут быть приведены к двум силам, при этом главные векторы и главные моменты этих систем сил не изменяются.

Рассмотрим дополнительную систему , силы которой пряморотивоположны силам системы:

, .

Тогда ,.

Системы сил (рис. 34а) и(рис. 34в) эквивалентны:

,

так как система может быть получена из системыотбрасыванием прямопротивоположных сил и.

Рассмотрим систему , состоящую из сил.

Главный вектор: .

Главный момент:

.

Согласно основной лемме статики систему сил можно заменить двумя силами. Тогда~. У эквивалентных систем сил равны главные моменты и главные вектор: поэтому

,

,

то есть – прямопротивоположные силы, которые можно отбросить. Таким образом:

,

или .

Теорема доказана.

8. Теория пар сил

8.1. Момент пары сил

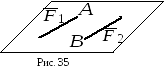Рассмотрим пару сил. По определению – это совокупность двух равных по величине и параллельных сил, направленных в противоположные стороны (рис. 35).

Плоскость, в которой лежит пара сил, называется плоскостью пары.Как уже отмечалось, главный момент пары не зависит выбора полюса и отличен от нуля.

Главный момент пары, не зависящий от выбора полюса, называется моментом пары. Обозначение:, или.

Момент пары – это свободный вектор, перпендикулярный плоскости пары, направленный в ту сторону, откуда видно, что пара стремится вращать тело против часовой стрелки, и равный по величине произведению одной из сил пары на кратчайшее расстояние между линиями действия сил пары (плечо пары).

Д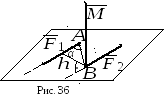ля доказательства этого утверждения рассмотрим пару(рис. 36).

8.2. Признак эквивалентности двух пар сил

Теорема.Для эквивалентности двух пар сил необходимо и достаточно, чтобы моменты этих пар были геометрически равны.

Доказательство.

Необходимость.

Дано: две пары сил иэквивалентны.

Следует доказать, что моменты этих пар геометрически равны:

.

Доказательство: Воспользуемся общим признаком эквивалентности двух систем сил и, согласно которому следует, что

,.

Но главный вектор любой пары равен нулю, главный момент пары равен моменту пары:

,.

Следовательно:

.

Достаточность.

Даны две пары сил и, причем моменты этих пар геометрически равны, то есть.

Доказать, что пары эквивалентны: ~.

Доказательство:

Главные векторы пар равны нулю и следовательно равны между собой . Моменты пар равны главным моментам пар и, по условию, равны между собой:

.

Тогда, согласно общему признаку эквивалентности двух систем сил, пары эквивалентны.