7. Общая постановка и разновидности задач математического программирования
Математическое программирование - обширная область знаний. Мы рассмотрели далеко не полностью один из разделов - линейное программирование.
Общая математическая схема задачи математического программирования такова: дана некоторая функция
z = f(x1, x2, . . . , xn) (7.1)
и некоторая система ограничений , наложенных на переменные x1, x2, . . . , xn:
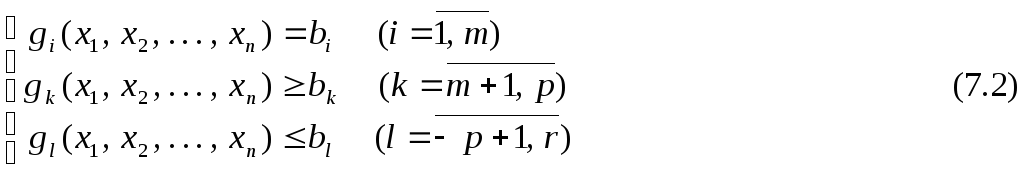
Требуется найти такой набор значений переменных x1, x2, . . . , xn, который удовлетворяет ограничениям (7.2), и при этом условии минимизирует или максимизирует функцию (7.1).
Если все фигурирующие в (7.1) и (7.2) функции линейны, то мы имеем ЗЛП. В противном случае получается задача нелинейного программирования.
Для задач нелинейного программирования нет такого универсального метода решения, каким является симплекс-метод для ЗЛП. Только для узких классов задач нелинейного программирования разработаны точные методы, основная масса решается приближенно.
В некоторых задачах математического программирования ОДР состоит из дискретного множества точек. Такие задачи называются дискретными оптимизационными задачами. Например, если в ЗЛП потребовать, чтобы переменные принимали только целые значения, то получится дискретная оптимизационная задача - задача целочисленного линейного программирования. Дискретные задачи, как правило, сложнее непрерывных. По задачам дискретной оптимизации в настоящее время проводятся интенсивные научные исследования.
Важной областью является и динамическое программирование. Здесь изучаются методы поэтапного решения оптимизационных задач. Такие методы используются в особенно сложных задачах. Например, при составлении плана работы завода на год целесообразно разбить год на месяцы и план работы на каждый месяц увязывать с планами на предыдущие и последующие месяцы.
Наконец отметим, что встречаются задачи математического программирования, в которых исходные данные являются случайными величинами. Такие задачи изучает стохастическое программирование. Стохастическое программирование использует теоретико-вероятностные, статистические и оптимизационные методы.
По математическому программированию написано уже много книг. Приводимая литература - незначительная часть их. Но в ней можно найти изложение основных положений математического программирования, а также ссылки на другие источники.
Литература
1. Крушевский А.В., Швецов К.М. Математическое программирование и моделирование в экономике.-К.: Вища шк., 1979
2. Кузнецов Ю.Н., Кузубов В.М., Волощенко А.Б. Математическое программирование.-М.: Высш.шк.,1980
3. Таха X. Введение в исследование операций. (В 2-х книгах).- М.:Мир,1985
4. Мину М. Математическое программирование. Теория и алгоритмы.-М.: Наука, 1990.
Содержание
РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ МЕТОДОМ ГАУССА – ЖОРДАНА........................................................
1.1. Основные понятия .......................
Приведение системы линейных уравнений к жордановой форме........
Понятие общего, частного и базисного решений.....
2.ОБЩИЕ СВОЙСТВА ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ ................
2.І. Пример задачи линейного программирования -
задача об использовании оборудования.....
2.2. Задача об использовании сырья..........
2.3. Задача составления рациона (задача о диете).
2.4. Общая постановка задачи линейного программирования
2.5. Геометрический метод решения ЗЛП.
2.6. Канонический вид ЗЛП.
2.7. Понятие опорного плана ЗЛП.
СИМПЛЕКСНЫЙ МЕТОД РЕШЕНИЯ ЗЛП
3.1. Общая характеристика и основные этапы симплекс –метода
3.2.Табличный вид ЗЛП. Симплекс - таблицы.
3.3. Условие оптимальности опорного плана.
3.4. Условие неразрешимости ЗЛП из-за неограниченности снизу на ОДР целевой функции.
3.5. Переход к новому опорному плану.
3.6. Табличный симплекс-алгоритм.
3.7. Отыскание исходного опорного плана ЗЛП методом искусственного базиса
3.8. Вырожденность опорного плана. Зацикливание.
4. Двойственность в линейном программировании ............................. 70
4.1. Экономическая интерпретация двойственных задач ................... 70
4.2. Понятие двойственной задачи ........................................................71
4.3. Теоремы двойственности .............................................................. 72
5. Транспортная задача......................................................................... ..........50
5.1. Задача о перевозках ................................................................ ..........50
5.2. Общая постановка транспортной задачи ..........................................51
5.3. Отыскание исходного опорного плана .......................................... 52
5.4. Циклы пересчета .............................................................................. 54
5.5. Потенциалы ........................................................................................57
5.6. Алгоритм решения транспортной задачи методом потенциалов ...60
5.7. Открытые транспортные задачи ......................................................63
6. ЦЕЛОЧИСЛЕННОЕ ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ .. 70
6.1. Общая постановка задачи целочисленного линейного программирования (ЗЦЛП).
6.2. Целочисленная задача об использовании сырья................... 70
6.3. Задача о рюкзаке. ........................................................71
6.4. Решение ЗЦЛП методом округления.
6.5. Метод ветвей и границ.
7. Общая постановка и разновидности задач математического программирования .......................................................................................
Литература .................................................................................................... 75
Содержание ................................................................................................... 89