3.7. Отыскание исходного опорного плана злп методом искусственного базиса

Чтобы начать решение ЗЛП симплекс-методом, нужно привести ее сначала к каноническому виду, а потом - к табличному. Табличный вид требует, чтобы система уравнений канонического вида была приведена к жордановой форме с неотрицательными правыми частями. Базисное решение такой жордановой формы будет исходным опорным планом ЗЛП.

Приведение системы линейных уравнений к жордановой форме не представляет труда, однако требование неотрицательности правых частей усложняет задачу. Кроме того, если ОДР задачи пуста, то жордановой формы с неотрицательными правыми частями не существует (хотя жорданову форму система линейных уравнений может иметь).

Систематическая процедура, которая либо обнаруживает неразрешимость ЗЛП из-за пустоты ОДР, либо приводит систему линейных уравнений канонического вида к жордановой форме с неотрицательными правыми частями (отыскивает исходный опорный план) называется методом искусственного базиса. Приступим к изложению этого метода.

Пусть ЗЛП записана в каноническом виде.

(3.5)

Прежде всего нужно сделать неотрицательными правые части системы (3.6). Этого можно добиться умножением на (-1) уравнений с отрицательными правыми частями. Итак, будем считать, что

(3.8)

Рассмотрим вспомогательную задачу, которая записывается следующим образом:

(3.9)

Переменные называютсяискусственными. Они образуют базис в жордановой форме (3.10), который называется искусственным базисом.

ОДР вспомогательной задачи непуста, так как ей принадлежит следующий набор значений переменных: (см.(3.10),(3.11),(3.12)(3.8)). Целевая функция (3.9), являющаяся суммой неотрицательных переменных, ограничена снизу на ОДР нулем:. Таким образом, для вспомогательной задачи ни одна из двух причин неразрешимости не имеет места, и, следовательно, вспомогательная задача разрешима. Так как система уравнений записана в жордановой форме с неотрицательными правыми частями, то мы можем привести вспомогательную задачу к табличному виду и решить симплекс-методом. После решения могут представиться два случая.

1. (3.I3)

Покажем, что тогда исходная задача (3.5 - 3.7) неразрешима из-за пустоты ОДР. Действительно, пусть, вопреки этому утверждению, есть допустимое решение исходной задачи. Тогда набор значений переменных

является, очевидно, допустимым решением вспомогательной задачи. Значение целевой функции F при этом допустимом решении равно 0, что противоречит (3.13).

2. (3.14)

Рассмотрим последнюю симплекс-таблицу для вспомогательной задачи. Выпишем соответствующую этой таблице жорданову форму с неотрицательными правыми частями. Здесь могут представиться две возможности:

а) среди базисных переменных нет искусственных. Тогда удалим из жордановой формы все члены, содержащие искусственные свободные переменные, получим жорданову форму с неотрицательными правыми частями для исходной задачи;

б) среди базисных переменных есть искусственные. Учитывая (3.9) и (3.14), можно утверждать, что в оптимальном плане значения всех искусственных переменных равны 0. Поэтому правая часть каждого уравнения, содержащего искусственную переменную в качестве базисной, равна 0, т.е. такое уравнение можно записать так:

(3.15)

Далее, если в уравнении (3.15) коэффициенты при всех переменных равны 0 (иначе говоря, оно фактически содержит только искусственные переменные), то удалим такое уравнение из жордановой формы. Если же уравнение вида (3.15) содержит какую-либо переменнуюс ненулевым коэффициентом, то поделим уравнение на коэффициент при, получим уравнение вида:

(3.16)

С помощью жордановой процедуры исключим из остальных уравнений системы. Так как правая часть уравнения (3.16) равна 0, то правые части остальных уравнений после исключенияне изменятся и останутся неотрицательными.

С помощью указанных приемов мы всегда можем получить жорданову форму с неотрицательными правыми частями, среди базисных переменных которой нет искусственных, и прийти, таким образом, к случаю а).

Пример I. Решить симплекс-методом

Задача записана в каноническом виде, однако правая часть второго уравнения системы отрицательна. Поэтому систему уравнений перепишем так:

Запишем вспомогательную задачу

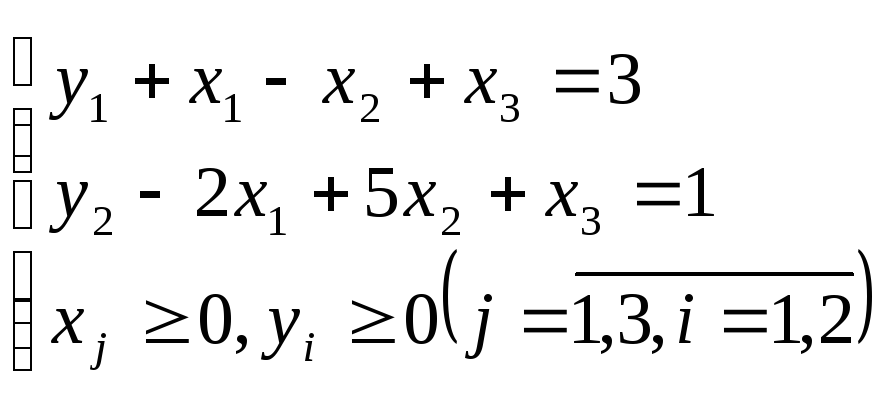
Решим вспомогательную задачу симплекс-методом. Для этого приведем ее к табличному виду

Табличный вид вспомогательной задачи таков:

Построим первую симплекс-таблицу (таблица 3.15)

Таблица 3.15

Б						Q
	1	-1	1	1	0	3
	-2	5	1	0	1	1
F	-1	4	2	0	0	4

Перейдем к новой симплекс-таблице (таблица 3.16)

Таблица 3.16

Б						Q
		0		1
		1		0
F		0		0

Переходим к следующей симплекс-таблице. Обратим внимание, что в качестве генерального столбца взят первый, а не третий столбец - это наше право!

Таблица 3.17

Б						Q
	1	0	2
	0	1	1
F	0	0	0	-1	-1	0

Мы достигли оптимального плана для вспомогательной задачи; при этом . Выпишем жорданову форму, соответствующую таблице 3.17:

Опустив искусственные переменные, получим жорданову форму с неотрицательными правыми частями для исходной задачи:

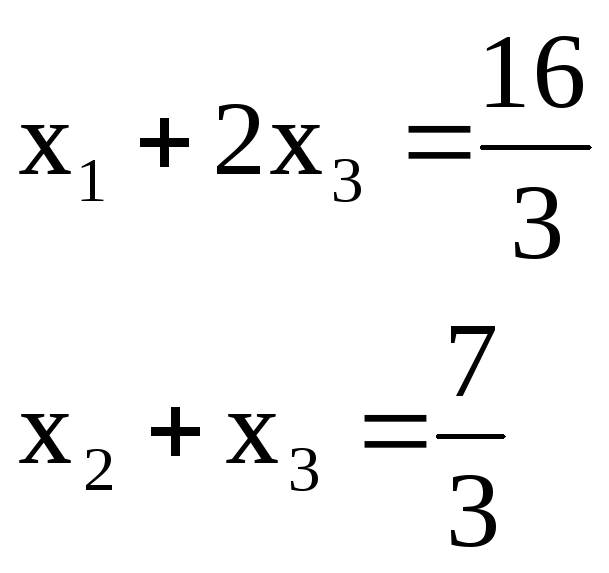
Теперь приступаем к решению исходной задачи. Приведем ее к табличному виду

Составим симплекс-таблицу для исходной задачи (таблица 3.18) и переходим к следующей таблице 3.19

Таблица 3.18

Б				Q
	1	0	2
	0	1	1
F	0	0	1

Таблица 3.19

Б				Q
	1	-2	0
	0	1	1
F	0	-1	0	-1

Получим оптимальное решение:

С целью частичного контроля правильности вычислений можно убедиться в том, что полученное решение является допустимым решением исходной задачи, значение целевой функции при котором равно -1.

Пример 2. Решить симплекс-методом

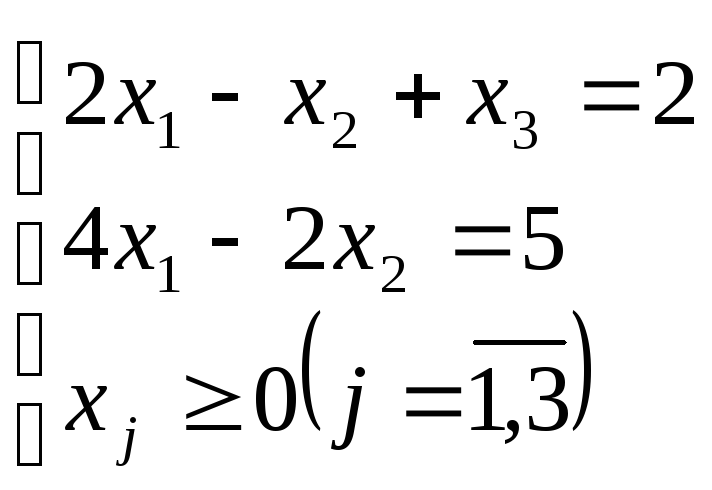
Составим вспомогательную задачу

Известными приемами приведем ее к табличному виду:

Заполним симплекс-таблицу (таблица 3.20)

Таблица 3.20

Б						Q
	2	-1	1	1	0	2
	4	-2	0	0	1	5
F	6	-3	1	0	0	7

Перейдем к новой симплекс-таблице (3.21)

Таблица 3.21

Б						Q
	1				0	1
	0	0	-2	-2	1	1
F	0	0	-2	-3	0	1

Получим оптимальный план. Значение целевой функции при оптимальном плане. Поэтому исходная ЗЛП неразрешима из-за пустоты ОДР.

Любопытно отметить, что система линейных уравнений исходной ЗЛП совместна и приводится к жордановой форме. Однако она не приводится к жордановой форме с неотрицательными правыми частями.

Сделаем еще одно полезное замечание. В рассматриваемом примере 2 можно было бы составить более простую вспомогательную задачу:

Дело в том, что цель введения искусственных переменных - получение жордановой формы с неотрицательными правыми частями для вспомогательной задачи. Здесь эта цель достигается с помощью одной искусственной переменной у . Допустимый базис состоит из переменных и у .