5.2.3. Признак оптимальности

При перемещении по циклу пересчета увеличиваются на эту величину значения переменныхX_ij в четных вершинах, а следовательно, увеличиваются и затраты на перевозку на C_ij. Одновременно уменьшаются на переменные в нечетных вершинах и на C_ij соответствующие им затраты. Отсюда следует, что значение критерия в новом, (k+1)-м решении можно определить по критерию в исходном решении и изменениям в клетках цикла:

или

, (5.15)

где

(5.16)

Здесь, как и в симплекс-методе, Δ_ij– относительная оценка переменнойX_ij, на которой построен цикл.Для базисных переменных оценка всегда равна нулю. Согласно (5.15)Δ_ijпоказывает, как изменится критерий (в какую сторону и насколько) при перемещении по циклу единицы груза ( =1).

Если Δ_ij>0, то введениеX_ij в число базисных приведет к уменьшению суммарных затрат. Если же Δ_ij<0, критерий возрастет, что противоречит цели. Следовательно, решение нельзя улучшить, когда среди оценок нет положительных, и поэтому признак оптимальности имеет вид

Δ_ij0. (5.17)

Если признак не выполняется, то новое решение целесообразно строить на основе клетки с максимальной оценкой (аналогично выбору в симплекс-методе при минимизации).

Вычисление оценок по формуле (5.16) требует построения цикла пересчета для каждой свободной клетки. Такой способ неэффективен для задач реальной размерности. Покажем, что возможен другой путь, исключающий построение циклов.

Поставим в соответствие каждому пункту отправления сбалансированной задачи некоторую величину U_i,i=1, 2,…,m, а каждому пункту назначения –V_j,j=1, 2,…,nтак, чтобы для базисных клеток выполнялись равенства

V_j -U_i=C_ij, i jбаз. (5.18)

Система (5.18) содержит m+ n-1 уравнений сm+ nнеизвестными. Присвоив одной из неизвестных некоторое произвольное значение, например, нуль, легко найти значения остальных. В таких случаях говорят о получении решения системы с точностью до постоянной величины. Дальше мы увидим, что произвольный выбор неизвестной и ее значения не влияет на конечный результат.

З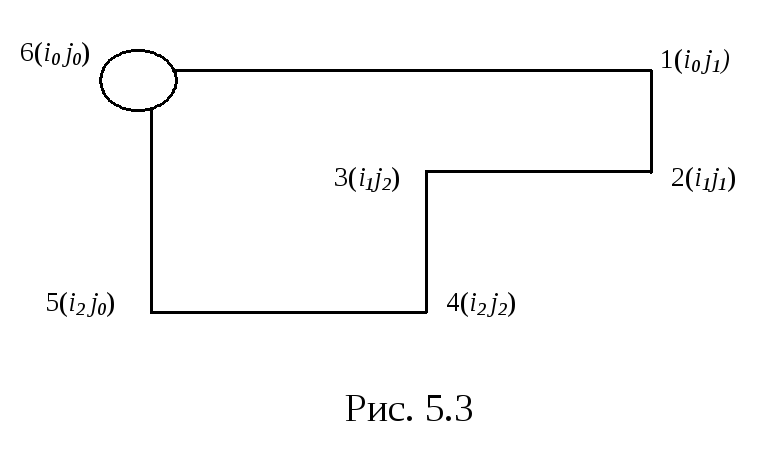наяU_i иV_j, можно вычислить относительную оценку для любого цикла в текущем плане перевозок. Покажем это на произвольно взятом цикле (рис. 5.3).

В скобках указаны индексы клеток (переменных), в которых расположены вершины цикла. Вычисляем относительную оценку свободной клетки i₀j₀ ( небазиснойпеременной X_iojo) по формуле (5.16):

Δ_iоjо=C_iоj1 - C_i1j1+ C_i1j2 - C_i2j2+ C_i2jо - C_iоjо.

Заменим в этом выражении затраты в базисных клетках согласно (5.18). Тогда получим

Δ_iоjо =V_j1 -U _iо -V_j1+U_i1+V_j2 -U_i1 -V_j2+U_i2+V_jо -U_i2 -C_iоjо =V_jo-U_io-C_iojo.

Выполненные сокращения не зависят от конфигурации цикла, так как все индексы кроме начальных входят в выражение два раза. Поэтому в итоге остаются только V_jo, U_io и C_iojo. Таким образом, для любой свододной клетки ijотносительная оценка может быть вычислена без построения цикла пересчета по формуле

Δ_ij=V_j-U_i-C_ij. (5.19)

Из сравнения (5.18) и (5.19) видно, что для базисных клеток Δ_ij=0.

Новые переменные U_iиV_jназываются потенциалами пунктов отправления и назначения соответственно, отсюда происходит название метода. Из формулы (5.19) следует, что значение постоянной величины при нахождении потенциалов из системы (5.18) не влияет на оценки.

Потенциалы можно интерпретировать как локальные цены. Если цена в пункте отправления iравнаU_i и груз из него доставляется в пункт назначения j по коммуникации ij, то локальная цена в ПН возрастет по отношению к ПО на величину транспортных затрат:

V_j=U_i+ C_ij. (5.20)

Из этого соотношения также следует, что в оптимальном решении не может иметь место неравенство

V_j >U_i+ C_ij,

так как оно означает, что локальная цена в пункте j выше, чем в случае прямой доставки из i в j.▲

Приведенный способ определения оценок через потенциалы пригоден для любого опорного плана перевозок. Однако учитывая структуру матрицы оценок (нули в базисных клетках), можно оценки нового плана получить минуя вычисления потенциалов простым преобразованием матрицы оценок предшествующего плана.

Рассмотрим конкретно преобразование матрицы ^(k)в матрицу^(k+1) на основе нового решения X^(k+1). Как отмечалось выше, новое решение получено вводом небазисной переменной с максимальной оценкой в ^(k). Пусть max _ij=_kr. В матрице^(k)отмечаем элементы, соответствующие базисным в новом решенииX^(k+1)(на рис. 5.4 помечены символом *), максимальную оценку отмечаем особо. Далее строим цепочку выделения. Она строится с особо отмеченного элемента, который соединяют с отмеченными в этой строке. Затем отмеченные элементы, попавшие в цепочку, соединяют с отмеченными в их столбцах. Далее снова проводим соединение по строкам, и так до тех пор, пока не оборвутся все ветви.

Рис.5.4

Элементы, попавшие в цепочку выделения, выделяют строку и столбец за исключением особо отмеченного элемента, который выделяет только строку. К выделенным столбцам прибавляем, а из выделенной строки вычитаем . Нетрудно увидеть, что при этом переменнойX_krбудет соответствовать нулевая оценка, как и тем перменным из решенияX^(k), которые сохранили статус базисных. Таким образом, преобразованная матрица соответствует новому опорному плану.

Провести выделение можно и иначе: сначала вычеркивать строку с максимальным элементом, затем вычеркивать столбцы, где есть элементы, отмеченные в этой строке, и т.д. Вычеркнутые строки и столбцы являются выделенными.