Методы классического анализа

Глава 3. Методы классического анализа

Когда величина является макси-

мальной или минимальной, в этот

момент она не течет ни вперед,

ни назад.

И. Ньютон

Рассматриваемые здесь методы известны с XVIII века. Они применимы к гладким или кусочно-гладким функциям, т.е. предполагается дифференцируемость на всей области определения функции за исключением отдельных точек.

3.1. Основные положения теории экстремумов

Опуская строгие определения и доказательства, приведем в этом разделе основные понятия и результаты теории экстремумов, имеющие прикладное значение.

Любая задача оптимизации может быть представлена как задача максимизации или как задача минимизации: для перехода от одного вида задачи к другому достаточно изменить знак целевой функции. Так, задача минимизации функции f=(x-5)² эквивалентна задаче максимизации функции f₁=-(x-5)², и наоборот.

Различают локальный и глобальный оптимумы (иногда применяют термины-синонимы: относительный и абсолютный оптимумы). Значение целевой функции, наилучшее на всей области D, называют глобальным оптимумом, а соответствующую точку X^* – точкой глобального экстремума или глобальным решением. Если же f(X^*) – наилучшее значение на окрестности точки X^* в области D, то говорят о локальном экстремуме.

Другой признак, по которому различают задачи и экстремумы, – наличие условий-ограничений, накладываемых на искомые переменные. Если модель задачи оптимизации не содержит условий (область D совпадает со всем евклидовым пространством), то имеем задачу на безусловный экстремум. В иных случаях, то есть при наличии ограничений, говорят о задаче на условный экстремум.

Очевидны следующие фундаментальные свойства задачи оптимизации. Для одной и той же целевой функции условный экстремум не может быть лучше безусловного. Сужение (расширение) множества D не может улучшить (ухудшить) глобальный экстремум.

Решение задачи оптимизации. Не для всех задач может быть найдено оптимальное решение. Простейший пример: нельзя найти минимум функции f=10-x как при отсутствии ограничений, так и при условии x³5. Для существования решения задачи оптимизации целевая функция и допустимое множество должны обладать определенными свойствами. В общем случае существование решения устанавливается следующей теоремой Вейерштрасса.

Теорема. Всякая функция, непрерывная на непустом замкнутом и ограниченном множестве, обладает наибольшим и наименьшим значениями, которые достигаются либо внутри множества, либо на его границе.

Условия теоремы гарантируют существование глобального оптимума, однако конкретная задача может иметь решение и на неограниченном или открытом множестве. На практике задачи исследования операций удовлетворяют условиям приведенной теоремы. Отметим, что теорема не требует непрерывности производных целевой функции.

Для определения глобального экстремума необходимо выявить и исследовать все точки, подозреваемые на экстремум. Эти точки называют также экстремальными или критическими. Из необходимых условий экстремума и теоремы Вейерштрасса следует, что возможны только три вида экстремальных точек:

- точки, в которых все частные производные первого порядка целевой функции одновременно обращаются в нуль, – стационарные точки;

- точки, в которых одна или большее число частных производных первого порядка перестают существовать (терпят разрыв);

- точки на границе допустимого множества.

Для случая функции одной переменной и a£x£b на рис.3.1 показаны все три вида точек: A,B,C - стационарные точки, D,E,F - точки разрыва производной, a, b - граничные точки. При этом в точке D имеем глобальный максимум, а в точке a - глобальный минимум.

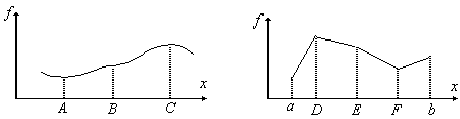
Рис.3.1

Очевидно, что не всякая "подозрительная" точка представляет интерес. Среди точек первых двух видов следует отбраковать те, в которых нет экстремума (например, точки B и E на рис.3.1) и которые не соответствуют искомому типу экстремума. С этой целью используются достаточные условия экстремума.

Для функции одной переменной имеется несколько вариантов достаточных условий. Если f(x^*±e) > f(x^*), где e - малая положительная величина, в точке x^* имеем локальный минимум. Сменив знак неравенства на обратный, получим условие максимума. Второй вариант заключается в проверке знака первой производной в точках (x^*-e) и (x^*+e): смена знака с минуса на плюс указывает на минимум, а с плюса на минус - на максимум. Наконец, для дважды дифференцируемой функции в точке x^* - минимум, если вторая производная положительна, и максимум, если она отрицательна. Для непрерывно дифференцируемой функции точке x^* соответствует экстремум, если в ней порядок первой ненулевой производной четный (в частности, второй).

При исследовании функции одной переменной могут оказаться полезными следующие простые свойства. У непрерывной функции максимумы и минимумы чередуются между собой. Поэтому, если между установленными точками максимума и минимума (или наоборот) имеется одна "подозрительная" точка, то в ней экстремума нет. Если функция строго возрастает на интервале , т.е.df/dx>0 на всем интервале, то x^*_max=b, а x^*_min=a. Это справедливо и при нестрогом возрастании, но тогда решение может быть не единственным. Если производная положительна в точке a, то x^*_max¹a, если же она отрицательна, то x^*_min¹a.

Определение экстремума облегчается, когда функция обладает свойством выпуклости или вогнутости. Это свойство устанавливается с помощью различных соотношений. Для одномерного случая справедливы следующие определения.

Функция f(x) выпукла на интервале [a, b], если для любых точек x₁, x₂Î[a,b] выполняется неравенство

. (3.1)

Функция f(x) выпукла на интервале [a, b], если для любых точек x₁,x₂Î[a,b] и произвольного числа [0, 1] выполняется неравенство

. (3.2)

Дважды дифференцируемая на интервале [a, b] функция f(x) выпукла, если на этом интервале

. (3.3)

Условия (3.1),(3.2) не требуют дифференцируемости функции. Их геометрический смысл иллюстрируется рис.3.2. Для выпуклой функции хорда, соединяющая две произвольные точки графика функции, лежит не ниже этой части графика. По условию (3.1) это устанавливается проверкой только в точке (x₁+x₂)/2, а согласно (3.2) при изменении  от 0 до 1 мы д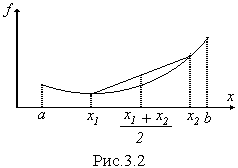вижемся от точкиx₂ к точке x₁ одновременно по графику функции (левая часть неравенства) и по хорде (правая часть неравенства), то есть проверка осуществляется на всем отрезке [x_1, x₂].

Изменение знаков неравенств в (3.1)-(3.3) на противоположные приводит к определению вогнутой функции. Если знаки неравенств заменить строгими, исключить случай x₁ = x₂ и граничные значения , то получим определение строго выпуклой или строго вогнутой функции. Очевидно, что если f(x) выпукла, то - f(x) – вогнута, и наоборот.

В теории оптимизации наиболее употребительно второе определение выпуклости. Оно легко обобщается на n-мерные функции: функция f(X) выпукла на выпуклом множестве D, если для любых двух точек X⁽¹⁾, X⁽²⁾ÎD и произвольного числа [0,I] выполняется неравенство

, (3.4)

где X⁽¹⁾, X⁽²⁾ - n-мерные векторы переменных.

Рассмотрим пример. Покажем, что функция f(x)=x² выпукла на интервале [-1,1]. Для этой функции условие выпуклости (3.2) принимает вид

.

Справедливость данного неравенства для =0 и =1 очевидна. Теперь докажем, что оно выполняется и для 0<<1. Возведя в квадрат левую часть и сделав элементарные преобразования, получим

или

.

Так как (1-)¹0, то из этого неравенства следует

или ,

что всегда справедливо, а при x₁¹x₂ имеем строгое неравенство. Таким образом, функция f(x)=x² является строго выпуклой.

Приведем некоторые полезные свойства выпуклых (вогнутых) функций на выпуклом множестве D.

1. Если функции f₁,f₂,...,f_m выпуклы на выпуклом множестве D и числа C₁,C₂,...,C_m не отрицательны, то функция также выпукла наD.

2. Если функции f₁,f₂,...,f_m выпуклы на множестве D, то выпукла на D и функция f(X)= f_i(X).

3. Если функция f(X) выпукла на множестве D, то для любого числа множество {XÎD|f(X)£a} является выпуклым.

4. Функция f(X), строго выпуклая (вогнутая) на D, имеет не более одного локального минимума (максимума). Любой локальный минимум (максимум) является глобальным.

5. Функция f(X), строго выпуклая (вогнутая) на D, достигает наибольшего (наименьшего) значения на границе множества D.

Теперь остановимся на особенностях исследования функций многих переменных. Определение стационарных точек даже функции одной переменной может вызвать затруднения, если необходимое условие приводит к сложному нелинейному уравнению (например, транс-цендентному). При n переменных необходимые условия дают систему n уравнений, в общем случае нелинейных. Решение системы нелинейных уравнений представляет собой самостоятельную сложную задачу, и здесь не обойтись без методов нелинейного программирования. Но последние можно применить непосредственно к функции, не используя необходимые условия, что нередко оказывается более эффективным.

Если стационарные точки найдены, то из них нужно выделить те, в которых функция имеет экстремум искомого типа. При этом недостаточно исследовать поведение функции по отдельным переменным. Так, например, для функции двух переменных малые отклонения от стационарной точки A как по x₁, так и x₂ приводят к уменьшению значения функции (рис.3.3), что, казалось бы, указывает на наличие в этой точке максимума. Однако в точке A нет ни максимума, ни минимума. 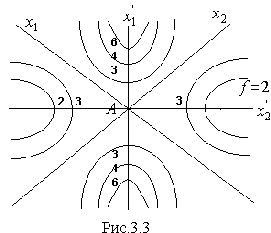Действительно, если повернуть оси координат на , то при отклонении поx₁¢ функция возрастает, а по x₂¢ - убывает. Такую точку называют седловой (аналог точки перегиба функции одной переменной). Точно так же в случае функции многих переменных стационарная точка является седловой, если функция ведет себя по-разному в окрестности этой точки. Таким образом, для установления экстремума необходимо исследовать всю окрестность стационарной точки, что можно сделать с помощью ряда Тейлора. В нем слагаемые первого порядка содержат первые производные, которые в стационарной точке равны нулю; слагаемые порядка выше второго стремятся к нулю быстрее слагаемых второго порядка. Следовательно, локальные свойства функции определяются производными второго порядка. Опуская выкладки, приведем достаточные условия экстремума в окончательном виде.

Составим квадратную матрицу n-го порядка из вторых частных производных (матрицу Гессе или гессиан):

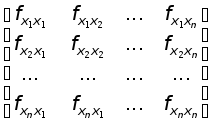
где - частные производные функцииf(X) по x_i и x_j в исследуемой стационарной точке. В стационарной точке имеем локальный минимум, если все диагональные определители матрицы Гессе положительны, то есть

D_i>0, i=1,n (3.5)

и локальный максимум, если

D_i<0, i=1,3,5,..., D_i>0, i=2,4,6,... (3.6)

В частности, для функции двух переменных условия минимума (3.5) имеют вид

(3.7)

а условия максимума (3.6)

(3.8)

Из приведенных выражений видно, что увеличение размерности функции ведет к непропорционально увеличивающемуся объему вычислений, необходимых для проверки достаточных условий. Еще большие трудности возникают при исследовании точек разрыва производных. Поэтому на практике часто отказываются от проверки достаточных условий, а точку глобального экстремума находят прямым сравнением значений функции во всех критических точках.

При решении задач на условный экстремум приходится выявлять также "подозрительные" точки третьего вида - точки на границе допустимой области. В задачах с одной переменной граница D - это точки на концах интервала, а в многомерном случае граница представляет собой линию или поверхность и ее исследование с целью выявления экстремальных точек становится весьма проблематичным.

Проиллюстрируем это на примере следующей задачи:

f(X) ® min, (3.9)

j₁(X)³0, (3.10)

j₂(X)³0, (3.11)

j₃(X)³0. (3.12)

Как решать такую задачу? Сначала найдем все точки, в которых может быть экстремум. Для этого нам потребуется решить ряд задач меньшей размерности.

Задача 1: найти экстремальные точки (далее - э.т.) внутри допустимой области. С этой целью решаем задачу на безусловный экстремум: f(X)®min. Предположим, что необходимые условия экстремума дают систему уравнений, которая поддается решению, и мы находим все э.т. Из них оставим только те, которые удовлетворяют условиям (3.10)-(3.12). Можно также отсеять точки, в которых не минимум, но для этого надо проверять достаточные условия.

Задача 2: найти э.т. на границе допустимой области, порождаемой ограничением (3.10). Для этого нужно решить задачу на условный экстремум

f(X)® min , j₁ (X)=0.

Здесь возможны два подхода: метод исключения и метод множителей Лагранжа. Применим первый из них (второй будет рассмотрен в следующем разделе). Из условия-равенства выразим одну переменную через остальные и подставим в f(X). Таким образом, задачу на условный экстремум с n переменными сводим к задаче на безусловный экстремум с n-1 переменной. Снова предположим, что нам удается разрешить систему необходимых условий для этой задачи и найти ее э.т. Оставляем только те из них, которые удовлетворяют неравенствам (3.11) и (3.12).

Задача 3 аналогична задаче 2, но рассматривается граница j₂(X)=0 и оставляемые э.т. должны удовлетворять неравенствам (3.10) и (3.12). Такова же и задача 4, в которой исследуются точки на границе j₃(X)=0.

Следующие три задачи заключаются в исследовании границ, образованных одновременно двумя ограничениями. Так, задача 5 имеет вид

f(X) ® min,

j₁ (X)=0,

j₂ (X)=0.

Предполагая, что два уравнения можно разрешить относительно двух переменных, и подставив выражения этих переменных в f(X), сведем задачу 5 к задаче на безусловный экстремум размерности n-2. Если она разрешима, получим соответствующие э.т., которые следует "просеять" через условие (3.12). Оставшиеся точки добавляем к ранее выделенным.

Задачи 6 и 7 аналогичны задаче 5, но границы порождаются другими парами условий. Еще одна граница образуется пересечением границ всех трех условий. Для ее исследования решаем задачу 8:

f(X)® min,

j₁(X)=0, j₂(X)=0,

j₃(X)=0.

Если три представленных уравнения разрешимы относительно трех переменных, то задача 8 сводится к задаче на безусловный экстремум размерности n-3. Так как при этом использовались все условия исходной задачи, то проверять найденные э.т. на принадлежность допустимой области не надо. Последняя задача 9 состоит в определении глобального минимума. Для этого вычисляются значения функции f(X) во всех точках, выявленных в задачах 1-8, и из них выбирается наименьшее.

Рассмотренный пример высвечивает все проблемы, возникающие при решении задачи математического программирования методом классического анализа. На каждом этапе решения нам приходилось делать оговорки типа "если", "предполагая". Невыполнение какой-либо одной из них создает неразрешимую ситуацию. Но и при возможности реализации приведенной схемы трудоемкость решения задачи весьма велика.

Завершая раздел, рассмотрим в качестве примера задачу исследования операций, которая может быть решена вышеприведенным способом. Это простая детерминированная задача управления запасами в следующей постановке. За период времени T склад должен поставить потребителю R единиц продукции, причем поставка должна быть равномерной. Пополнение склада производится партиями без задержки с момента заказа. Допустим дефицит продукции на складе, но он вызывает потери. Известны: С₁ - затраты на хранение единицы продукции в единицу времени; С₂ - потери от дефицита единицы продукции в единицу времени; С₃ - затраты на пополнение склада одной партией (не зависят от объема партии).

Требуется определить, как часто нужно пополнять склад и в каком объеме.

Построим математическую модель задачи. Характер изменения запасов на складе и продукции у потребителя показан на рис.3.4.

Неизвестными на графике являются: q - объем партии; s - максимальный запас на складе; t_ц - продолжительность одного цикла, t₁ - часть времени цикла, в течение которого запас есть; t₂ - часть времени

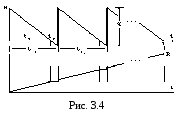
цикла, когда имеется дефицит. За критерий оптимальности принимаются суммарные затраты, связанные с запасами.

Общие затраты определим как затраты за цикл, умноженные на число циклов m. Затраты за цикл следующие:

• затраты на хранение за время ,

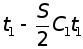• потери от дефицита в течение времени ,

• затраты на пополнение склада одной партией - С₃.

Таким образом, суммарные затраты

. (3.13)

Учитывая, что , получаем

. (3.14)

Из подобия треугольников (см. рис.3.4) и (3.14) имеем

Подставив выражения t₁, t₂ и m в (3.13), приходим к окончательному виду целевой функции

. (3.15)

Формализация задачи завершается записью ограничений, которые вытекают из физического смысла переменных:

s³0, q³0, q-s³0. (3.16)

Таким образом, поставлена задача оптимизации с двумя переменными и тремя условиями. Малая размерность, дифференцируемость целевой функции и простота условий позволяют решать эту задачу методами классического анализа. Здесь мы не будем приводить решение, оставляя его для самостоятельной работы (см. раздел 3.3).