Транспортные задачи

Глава 5. Транспортные задачи

Задачи, называемые транспортными, составляют большой подкласс распределительных задач. С содержательной стороны они не обязательно связаны с доставкой или перевозкой грузов, а выделяются из других задач особой структурой математической модели. Поэтому правильнее говорить о моделях транспортного типа.

Если удельные затраты на перевозку не зависят от количества перевозимого груза, транспортная задача описывается линейной моделью. При этом ее особенности позволяют применять специальные методы линейного программирования, которые более эффективны, чем универсальные. Ниже рассматриваются только линейные задачи.

5.1. Основные модели транспортных задач

5.1.1. Простейшая транспортная задача (т-задача)

Эта задача является основополагающей для всех транспортных задач. Пример такой задачи приведен в разд. 4.9.

В общем случае исходными данными являются:

m – число пунктов отправления (ПО) или производства;

n – число пунктов назначения (ПН) или потребления;

C_ij – затраты на перевозку единицы груза из пунктаi в пункт j, ij;

a_i – количество груза в пунктеi, i (возможности ПО);

b_j – потребность в грузе в пунктеj, j.

Критерием задачи являются суммарные затраты на перевозку. Безотносительно к значениям a_iиb_jмодель записывается в виде

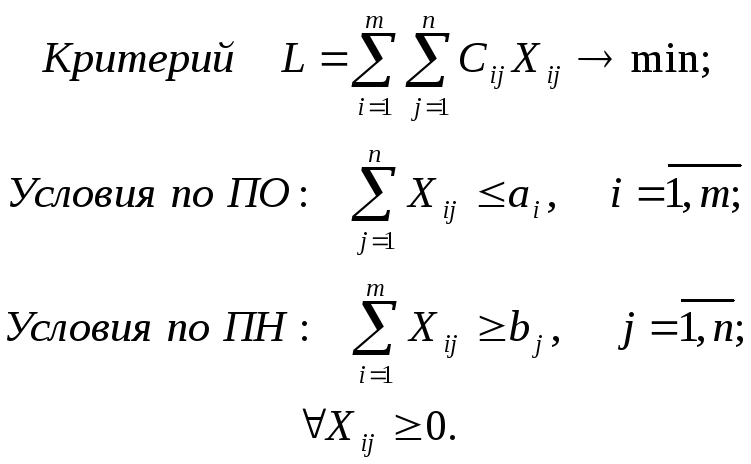
Однако такая запись модели корректна только тогда, когда Напомним, что задача, в которой суммарные потребности равны суммарной возможности, то есть

(5.1)

называется сбалансированной или закрытой. Как будет показано в этой главе, любая несбалансированная задача легко приводится к закрытой. Поэтому здесь рассмотрим только сбалансированную задачу:

(5.2)

(5.3)

(5.4)

X_ij  0. (5.5)

Элементы модели:

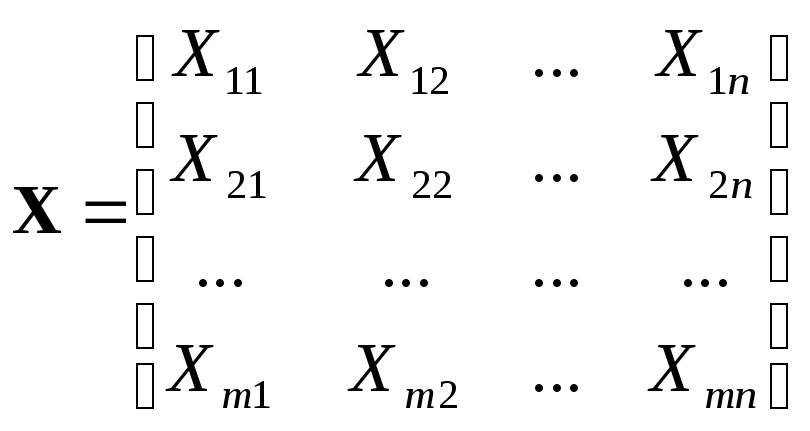– матрица перевозок;

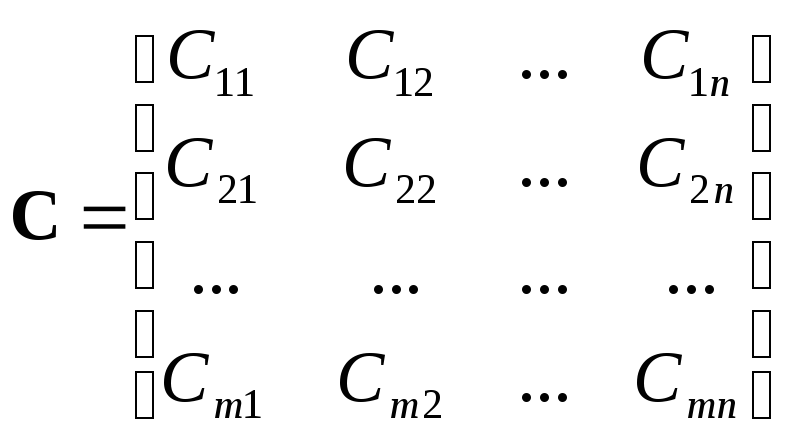– матрица транспортных затрат;

a=(a₁, a₂, . . . , a_m) – вектор возможностей ПО;

b=(b₁, b₂, . . . , b_n) – вектор потребностей ПН.

Отметим особенности рассматриваемой задачи:

• Модель содержит две группы условий, размерность которых равна соответствующему числу ПО и ПН; число переменных равно произведению mn;

• Все коэффициенты при переменных в условиях (5.3), (5.4) равны единице;

• Каждая переменная входит в условия ровно 2 раза, один и только один раз в группу (5.3) и также один раз в группу (5.4);

• Задача имеет простые условия разрешимости, которые определяются следующей теоремой.

Теорема.

Для разрешимости Т-задачи необходимо и достаточно, чтобы она быласбалансированной.

Замечание. Теорема справедлива при конечных значенияхС_ij.

Приведем доказательство.

Необходимость доказывается исходя из того, что задача (5.2)-(5.5) разрешима. В этом случае все условия задачи выполняются. Просуммируем условия (5.3) по i, а условия (5.4) по j:

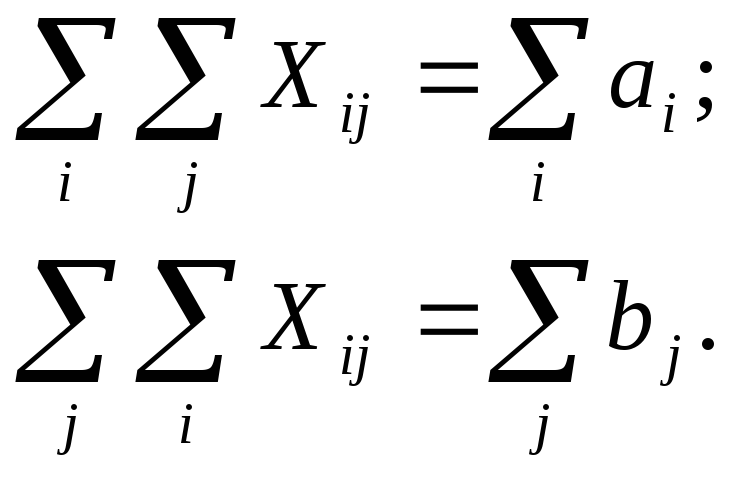
Так как левые части равенств равны, то равны и правые. Таким образом, в разрешимой задаче всегда имеет место формальный баланс возможностей и потребностей.

Достаточность доказывается конструктивным способом.

Вспомним, что задача линейного программирования всегда разрешима, если допустимое множество – выпуклый многогранник, то есть непустое и ограниченное.

Ограниченность переменных снизу задана явно, а ограничение сверху следует из конечности всех a_i и b_j, больше которых переменные быть не могут. Следовательно, множество ограничено.

Теперь покажем, что оно непустое. Для этого достаточно найти хотя бы одно допустимое решение. Одно из таких решений всегда можно построить, если задача сбалансирована, следующим образом:

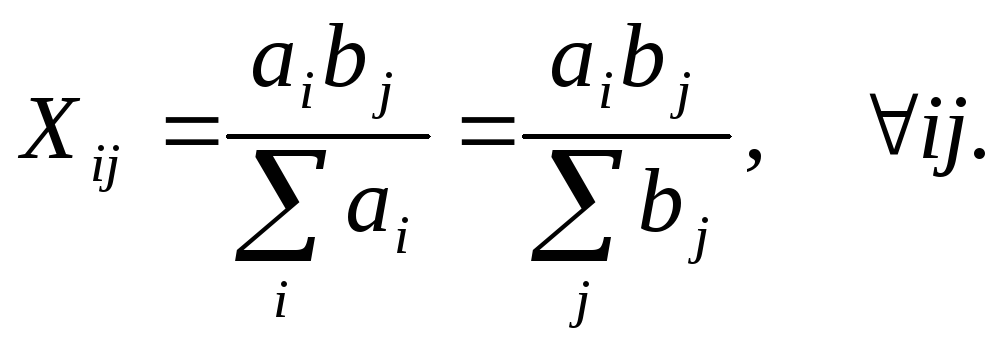(5.6)

Очевидно, что оно неотрицательно. Остается проверить выполнение основных условий задачи. Подставив (5.6) в левую часть(5.3), получим:

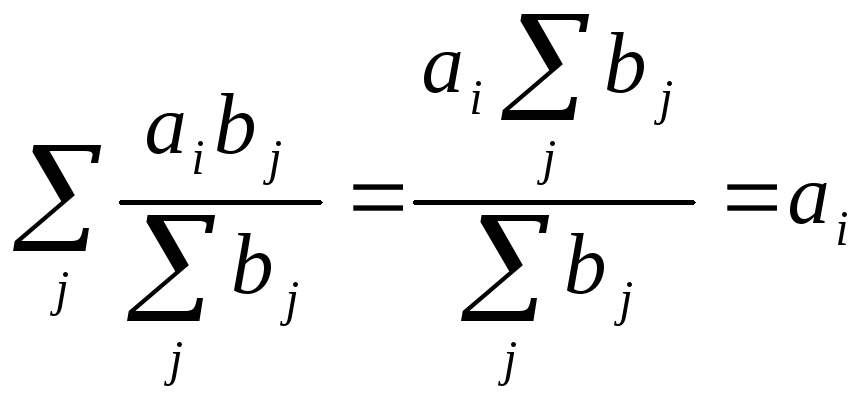решение удовлетворяет условиям (5.3).

Подставив первый вариант (5.6) в (5.4), также убеждаемся в выполнении этих условий:

.

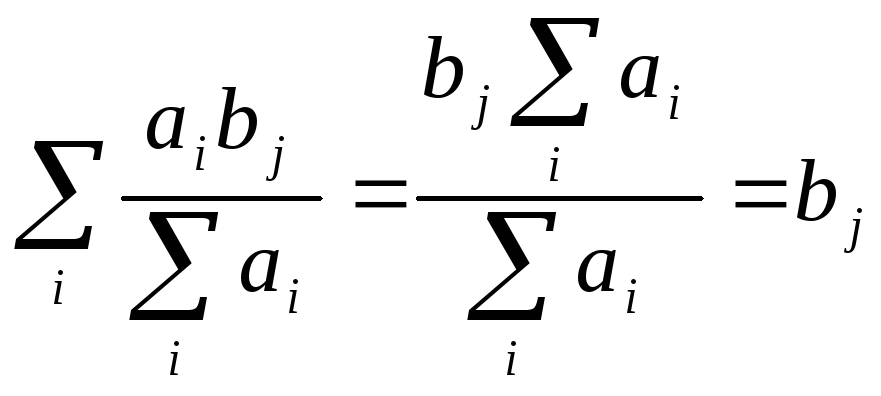Таким образом, допустимое множество сбалансированной задачи непустое и ограниченное, а, значит, задача всегда разрешима. ▲

Условия (5.3), (5.4) – линейно зависимы из-за сбалансированности задачи. Действительно, пусть известны все равенства (5.3) и (n-1) равенство (5.4). Просуммируем отдельно первые и вторые и затем из первой суммы вычтем вторую. В результате получим недостающее равенство, описывающее пункт потребления, не включенный в исходную систему (5.4). Можно строго показать, что число линейно-независимых уравнений или, иначе, ранг системы (5.3), (5.4) равенm+n-1. Следовательно, такую размерность имеют базис и базисное решение Т-задачи.