5.5. Решение задачи по критерию времени

Как было показано в разд. 5.1.5, такая задача исходно является нелинейной, но может быть легко преобразована к линейной. Однако получаемая линейная модель громоздка и для нахождения решения требует применения универсальных методов линейного программирования.

Поэтому может оказаться целесообразным обратиться к приближенным, но более простым методам решения. Один из них рассмотрен ниже. Он использует идеи методов решения обычных транспортных задач и заключается в следующем.

Любым из способов строится начальный план перевозок. Затем определяется текущее значение критерия Т⁽⁰⁾ как максимальное время в занятых клетках (x_ij>0). Далее рассмотрим действия в цикле.

Пусть на k-й итерации получен план со значением критерияТ^(k).Оно может быть уменьшено, если освободить клетку сt_ij= Т^(k). С этой целью на клетке строится разгрузочный цикл так, чтобы в нечетных вершинах выполнялось неравенство t_ij<Т^(k), а в четных –x_ij>0 (исходная вершина – четная). Очевидно, что такие правила позволяют в общем случае строить более одного цикла на выбранной клетки. В цикле вычисляется ₀ как минимальная перевозка в четных вершинах. Вычитая ₀ вчетных вершинах и прибавляя в нечетных, получаем новый план. Если клетка с максимальным временем была единственной и перевозка в ней стала равна нулю, новый план улучшил значение критерия. Если клетка не обнулилась, то на ней строится другой разгрузочный цикл. В случае нескольких клеток со временемТ^(k)для улучшения критерия необходимо разгрузить все. Решение завершается, когда нельзя разгрузить клетку (клетки), определяющую значение критерия.

Естественно, что рассмотренный метод не гарантирует получение оптимального решения.

5.6. Транспортные задачи в сетевой постановке (транспортные сети)

Транспортную задачу можно представить в виде ориентированного графа с одним истоком (в него не входит ни одна дуга) и с одним стоком (из него не выходят дуги), который называют в этом случае сетью. Вершинам графа ставятся в соответствие пункты отправления, назначения и промежуточные пункты. Основной параметр вершины – количество груза. Дуги отображают коммуникации. Им могут быть приписаны такие параметры как количество груза, затраты на перевозку, пропускная способность.

Исходный граф транспортной задачи легко сводится к сети с одним стоком и одним истоком путем введения фиктивных пунктовt (исток) и s (сток). Фиктивным дугам приписываются значения параметров: d_ti=a_i, d_js=b_j, C_ti=C_js=0. Пример сети транспортной задачи без промежуточных пунктов приведен на рис. 5.6.

Модель Т_d-задачи в сетевой постановке имеет вид:

C_ijx_ijmin; (5.29)

kt, ks; (5.30)

(5.31)

В сбалансированной транспортной задаче

Z=a_i=b_j; (5.32)

0x_ijd_ij. (5.33)

Равенства (5.30) отражают условия баланса для всех пунктов кроме источника и стока. Баланс для последних представлен уравнением (5.31). В модели использованы обозначения: –множество дуг, входящих в вершинуkи выходящих из нее, Z – новая величина, называемаяпотоком сети.

Наибольший интерес представляет постановка задачи, в которой критерием является поток сети:

Z max; (5.34)

kt, ks; (5.35)

(5.36)

0x_ijd_ij. (5.37)

Задача (5.34) – (5.37) называется задачей о максимальном потоке. Она имеет большое практическое значение. Для нее разработаны алгоритмы, которые эффективнее методов решения транспортных задач. Они работают непосредственно с сетью как разновидностью графов.

В связи с этим напомним понятие разреза графа (сети), которое используется в основополагающей теореме Форда-Фалкерсона.

Пусть дан ориентированный граф G=(V,U), гдеV и U - множества вершин и дуг соответственно. Разрезом сети на подмножестве вершин AV, A, AV, tA, sV\A называется множество дугijU таких, чтоiA  jV\A. Обозначим егоP(A). Сумма пропускных способностей дуг разреза называетсявеличиной(пропускной способностью)разреза:

Пример 5.5. Построим один из разрезов сети, приведенной на рис.5.7.

ЕслиA={t,1,2,3}, то разрезом будет множество дуг P(A)={1,4; 1,6; 2,5; 3,6}, а его величина определяется как d(A)=d₁₄+d₁₆+d₂₅+d₃₆. Дуги, составляющие этот разрез, выделены жирными линиями.▲

Разрез сети, имеющий минимальную пропускную способность, называется минимальным разрезом.

Можно показать, что задачи максимизации потока и минимизации величины разреза являются двойственной парой. Из этого факта следует Теорема Форда и Фалкерсона:

Величина потока сети (от истока к стоку) не превосходит пропускной способности минимального разреза и существует максимальный поток, величина которого равна пропускной способности минимального разреза.

Методы решения задачи о максимальном потоке основаны на последовательном увеличении потока при соблюдении условий (5.35)-(5.37). При этом легко увидеть аналогию с перемещением по циклу в методах решения транспортных задач.

Аналогом цикла пересчета является увеличивающая цепь. Это цепь, соединяющая исток и сток, все дуги которой допустимые. Дуга является допустимой увеличивающей, если ее направление совпадает с направлением потока и поток на ней меньше пропускной способности, то есть x_ij<d_ij. Дуга считается допустимой уменьшающей, если направление дуги противоположно потоку и x_ij >0.

На увеличивающей дуге поток может возрасти на величину _ij=d_ij-x_ij, а на уменьшающей дуге возможно снижение потока, равное_ij=x_ij. Следовательно, максимальное допустимое изменение величины потока по увеличивающей цепи определяется как минимальное из возможных:

₀=(5.38)

Таким образом, максимальный поток сети может быть определен по следующему алгоритму.

1. Задать начальную величину потока, обеспечиваемую потоками дуг при выполнении условий (5.35)-(5.37).

Примечание. Очевидно, что в качестве начального всегда можно взять нулевой поток.

2. Построить увеличивающую цепь. Если построить невозможно, то решение завершено.

3. По формуле (5.38) вычислить ₀.

4. Переместить вдоль цепи ₀, прибавляя к потокам на увеличивающих дугах и вычитая из потоков уменьшающих дуг. В результате поток сети увеличивается на ₀. Перейти на шаг 2.

П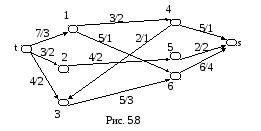ример 5.6. Определить максимальный поток сети на рис. 5.8. Пропускные способности дуг показаны у стрелок перед косой чертой.

Задаем начальный поток. Значения начальных потоков дуг даны за косой чертой, они удовлетворяют условиям задачи. Величина потока сети Z⁽⁰⁾=7.

Первая итерация.

Строим увеличивающую цепь. Она показана на рис. 5.8 утолщенными линиями. Определяем приращение потока: ₀ = min(7-3, 5-1, 6-4)=2. Увеличиваем потоки дуг цепи на 2 (рис. 5.9).Z⁽¹⁾= Z⁽⁰⁾ + ₀=7+2=9.

Вторая итерация.

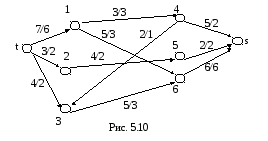Строим увеличивающую цепь{t,1; 1,4; 4,s} (рис. 5.9). ₀ = min(7-5, 3-2, 5-1)=1.Увеличиваем потоки по дугам цепи на ₀ (рис. 5.10). Z⁽²⁾= Z⁽¹⁾ + ₀ = 9+1=10.

Третья итерация.

Новая цепь состоит из увеличивающих дуг t,3 и 4,s и уменьшающей дуги 4,3 (рис. 5.10). ₀ = min(4-2, 1, 5-2)=1. Изменяем потоки: на дугах t,3 и 4,s увеличиваем, а на дуге 4,3 уменьшаем на величину ₀. Тогда получаем Z⁽³⁾= Z⁽²⁾ + ₀ = 10+1=11 (рис. 5.11).

Так как увеличивающую цепь построить нельзя, последнее решение является оптимальным. Максимальный поток сети равен 11.

Минимальный разрез рассмотренной сети соответствует множеству вершин А={t,1,2,3,5,6}, то есть P(A)={1,4; 5,s; 6,s}. Его пропускная способностьd(A)=d₁₄+d_5s+d_6s=3+2+6=11 равна величине максимального потока, что согласно теореме Форда-Фалкерсона также является признаком оптимальности найденного решения.