5.1.4. Многоиндексные задачи
Для учета дополнительных условий перевозки вводятся переменные с числом индексов более двух. В таких случаях говорят о многоиндексных транспортных задачах. Например, если существенное значение имеет вид транспорта, то в модели используются переменныеXijk, означающие количество груза, перевозимое изi-го пункта вj-йk-ым видом транспорта. Модель трехиндексной задачи зависит от конкретных условий. Если в исходных данных имеем производительность каждого вида транспортаpk и не учитываются пропускные способности, то задача описываетсятрипланарной моделью:
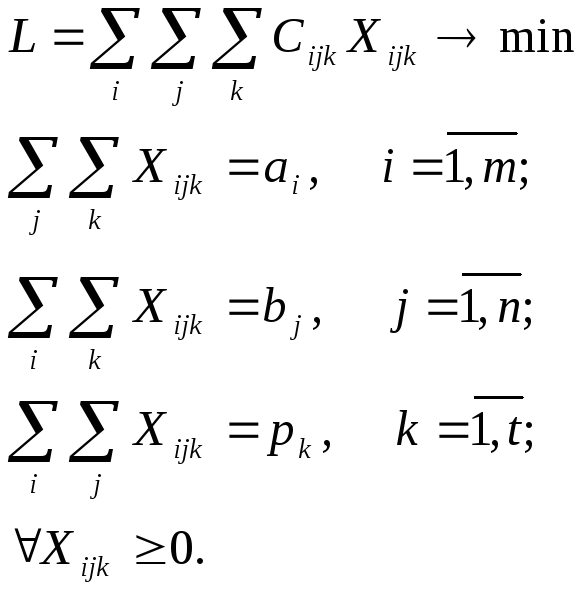
Она идентична Т-задаче. Отличие лишь в числе переменных и групп условий. Поэтому каждая переменная входит в модель ровно три раза, а сбалансированность, как необходимое и достаточное условие разрешимости задачи, записывается в виде
Если транспортные средства принадлежат разным перевозчикам, то в модели будут фигурировать четырехиндексные переменные Xijkl, гдеl – индекс перевозчика.
Дальнейшая детализация условий транспортировки может потребовать переменных с пятью и более индексами. В ряде случаев многоиндексные задачи удается свести к двухиндексным.
5.1.5. Транспортные задачи по критерию времени
При осуществлении перевозок определяющим показателем могут быть не затраты, а время доставки. Характерными примерами являются чрезвычайные ситуации, перевозка раненых, скоропортящихся продуктов и т. п. В таких задачах главное – как можно быстрее доставить все грузы. Тогда вместо матрицы транспортных затрат дается матрица времени [tij], а критерий выражает время завершения всех перевозок:
где максимум берется по коммуникациям, на которых перевозки больше нуля. Предполагается, что перевозки между всеми пунктами начинаются одновременно и ведутся параллельно. Условия задачи записываются как и в случаях с критерием-затратами. Однако здесь критериальная функция нелинейна, что принципиально отличает эту задачу от ранее рассмотренных. В то же время она легко преобразуется к линейному виду, и решение задачи может быть получено любым универсальным методом линейного программирования. Один приближенный метод рассмотрен в разд. 5.5.▲
Для решения транспортных задач применяют специальные методы, которые учитывают их особенности и поэтому более эффективны, чем универсальные. К ним относятся распределительный метод, метод потенциалов, венгерский метод, метод Глейзала и др. Основными являются методы венгерский и потенциалов. Они применяются для решения задач как типа Т, так и Тd. Ниже рассматривается второй из них.
5.2. Метод потенциалов
Концепция метода потенциалов та же, что и в симплекс-методе. Оптимальное решение ищется путем последовательных переходов от одного базисного решения (опорного плана) к другому с лучшим значением критерия. Но все шаги алгоритма выполняются проще, чем в симплекс-методе. В то же время метод потенциалов имеет много общего с распределительным методом и в связи с этим его иногда называют модифицированным распределительным методом.
Сначала рассмотрим метод применительно к Т-задаче, а затем сделаем дополнения, позволяющие решать Тd-задачу.
5.2.1. Построение начального плана перевозок
Как было показано выше, размерность базисного решения или плана перевозок равна m+n-1, где m и n – число ПО и ПН сбалансированной задачи. Если задача открытая, то сначала ее необходимо сбалансировать.
Следует также иметь в виду, что в транспортных задачах вырожденность базисного решения встречается очень часто. В задаче заведомо будут вырожденные решения, если имеются такие неполные группы пунктов отправления и назначения, что суммарная возможность первых равна суммарной потребности вторых. Вырожденным может оказаться и начальное решение.
Для построения начального плана перевозок применяют правила северо-западного угла, минимального элемента и алгоритм Фогеля. Последний можно применять и как приближенный метод решения Т-задачи.
Здесь мы рассмотрим только первые два способа. Хотя по аналогии легко предложить и другие правила. При этом важно соблюдать принцип: очередной переменной, включаемой в план, присваивать максимально допустимое значение. Этим обеспечится построение базисного решения.