Макроскопическая работа и теплота

При взаимодействии термодинамической системы с окружающей средой происходит обмен энергией. Возможны два способа передачи энергии от системы к внешним телам и от внешних тел к системе. Первый способ связан с совершением работы, а второй с теплообменом.

При совершении работы изменяются внешние параметры системы. Работа как процесспредставляет собой макроскопическую передачу энергии в упорядоченной форме путем взаимного действия системы и внешних тел друг на друга.Работа как результат– это энергия, переданная системой указанным способом.

При теплообмене (без совершения работы) внешние параметры остаются неизменными. Энергия, переданная системе в результате теплообмена от окружающих тел, называется количеством теплоты, полученным системой в таком процессе.

Работа и количество теплотыявляются функциями процесса, который совершает система. Состоянию системы не соответствует какое либо значениеи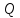. По этой причине не имеет смысла говорить о запасе количества теплоты или работы в теле.

Определим работу, которую совершает газ, находящийся в цилиндрическом сосуде с поршнем (рис. 8.1), в результате его квазистатического расширения с изменением объема от до. В данном случае– это единственный изменяющийся внешний параметр системы.

Рис. 8.1.

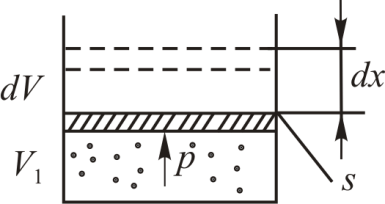
Для вычисления работы надо прежде всего найти силу, действующую на поршень. Газ действует на поршень, площадь сечения которого , с силой давления. Рис.8.1.

Бесконечно малая или элементарная работа, совершаемая газом при перемещении поршня на , равна. Полную макроскопическую работу можно получить интегрированием согласно (8.5).

Положительной считается работа, совершаемая газом против внешних сил при его расширении: ; отрицательной – совершаемая над газом внешними силами при его сжатии:.

На диаграмме (рис. 8.2) величина макроскопической работы выражается площадью под линией, изображающей определенный

процесс.

Величина зависит от процесса или «пути», которым перевели систему в данное состояние. На рис.8.2 видно, что работа по замкнутому контуру, т.е. работа за цикл, не равна нулю.Работа не является функцией состояния.

Говоря о теплообмене, отметим, что он может осуществляться путем передачи энергии макросистеме от внешних тел к, от внешних тел при непосредственном контакте с ними, а так же через излучение. Количество теплоты может, как сообщаться системе, так и забираться от неё. Количествотеплоты, полученное системой, не является функцией состояния.

Рис. 8.2

С молекулярно-кинетической точки зрения количество теплоты – это мера обмена энергией между хаотически движущимися молекулами взаимодействующих макроскопических тел.

В заключение еще раз подчеркнем, что можно говорить о приращении внутренней энергии, но нельзя говорить о приращении работы или теплоты. Можно говорить только о количестве теплоты, полученном системой, и совершенной ею работе в том или ином процессе.

8.6. Калорическое и термическое уравнения состояния

Эти термины используются в термодинамике для именования хорошо известных вам уравнений. Калорическое уравнение состоянияилиуравнение энергии– это, конечно,.Термическое уравнение состояния– это обобщенное уравнение состояния, выражающее функциональную связь между макроскопическими параметрами системы, одним из которых является температура. Для систем, у которых внешним параметром является только объем, это уравнение определяется функциональной зависимостью.

В дальнейшем мы убедимся, что термическое и калорическое уравнения состояния не являются независимыми. Они связаны дифференциальными уравнениями в частных производных. Вывести уравнения состояния на основе начал термодинамики нельзя. Они или находятся из опыта или выводятся методами статистической физики. Для идеального газа термическим уравнением состояния является уравнение Клапейрона-Менделеева, калорическим –.

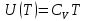Из термического уравнения состояния можно вывести три термических коэффициента. Термические коэффициенты– это величины характеризующие изменение какого-либо параметра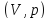, входящего в термическое уравнение состояния макросистемы, в зависимости от другого параметра в определённом термодинамическом процессе. Формулы для этих коэффициентов приведены на схеме 8.6.1.

Термические коэффициенты описывают важные в практическом отношении свойства различных веществ. Из (8.6) следует, что если известны два любых термических коэффициента, то можно вычислить третий. Это особенно актуально для нахождения у твердых тел и жидкостей, поскольку их экспериментальное определение в значительной степени затруднено, так как эти тела практически невозможно нагреть без изменения их объема.

Схема 8.6.1.

Подобно трём термическим коэффициентам употребляются также три термодинамических коэффициента(см. схему 8.6.2).

Схема 8.6.2.

Следует отметить, что в учебной литературе по термодинамике многие авторы не делают строгого разграничения между термическими и термодинамическими коэффициентами, за исключением И.П. Базарова [1]. Зачастую коэффициенты обеих групп называют термическими или даже тепловыми.

Контрольные вопросы

1. Какова функциональная роль каждого из четырех начал термодинамики?

2. Сформулируйте нулевое начало. Какова область его применимости?

3. Каким образом вводится температура в термодинамике?

4. Как следует понимать свойство транзитивности термодинамического равновесия? В чем состоит его практическое значение?

5. Какой процесс называется: а) термодинамическим; б)квазистатическим; в) релаксацией; г) обратимым в узком смысле слова; д) обратимым в широком смысле слова?

6. Каким образом можно установить является данная термодинамическая величина функцией состояния или нет?

7. Дайте микроскопическую и макроскопическую трактовку внутренней энергии системы.

8. Определите следующие понятия: работа как процесс и работа как результат.

9. Что называется количеством теплоты? Дайте микроскопическую трактовку этому понятию.

10. Какие из перечисленных ниже величин являются функциями состояния: ?

11. Запишите формулу для вычисления работы, совершенной газом, в результате его квазистатического расширения. Поясните ее смысл с помощью графика процесса.

12. Что характеризуют термические коэффициенты? Запишите формулы для термических коэффициентов расширения, сжатия и давления, а также соотношение связывающее их между собой.

ЛЕКЦИЯ 9

ПЕРВОЕ НАЧАЛО ТЕРМОДИНАМИКИ