Матан. М.В.Ишханян

Точки разрыва функции классифицируются в зависимости от того, какое условие непрерывности нарушено:

собой пределы. Такая точка называется точкой неустранимого разрыва первого рода или точкой разрыва с ко-

нечным скачком функции (говорят, что f ( x) терпит в

точке x0 скачок);

(3)Если в точке x0 функция f ( x) имеет бесконечный предел справа или слева или один из этих пределов не существует, то точка x0 называется точка разрыва второ-

го рода.

Пример 1 Исследовать на непрерывность функцию

деление f ( x) , являются непрерывными элементарными функ-

циями, то функция f ( x) непрерывна всюду кроме, может быть,

точек «склейки» x1 = -1 и x2 = 2 . Исследуем поведение функции в окрестности этих точек:

а) Рассмотрим точку x1 = -1 .

80

f (-1) = -(-1) =1.

Так как f (-1- 0) = f (-1+ 0) = f (-1) =1 , то функция непре-

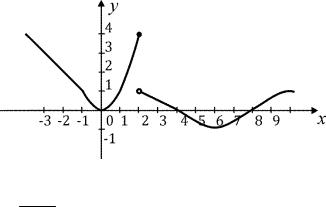
Так как f (2 - 0) = f (2) = 4 ¹ f (2 + 0) =1, то f ( x) в точке x2 = 2 терпит разрыв первого рода. Сделаем чертёж (рис.4.1).

1

f ( x) = 2x2 (x2 −1) . Сделать эскиз графика.

Решение Функция является элементарной, поэтому непрерывна во всех точках, кроме точек x1 = -1 , x2 = 0 , x3 = 1 , в которых она не определена. Найдём характер разрыва в этих точках.

81

а) Рассмотрим точку x1 = −1 .

x1 = −1 терпит разрыв второго рода. б) Рассмотрим точку x2 = 0 .

Так как f (1− 0) = +0 , f (1+ 0) = +∞ , то x3 = 1 является точкой разрыва второго рода.

Для построения эскиза графика исследуем поведение функции при x → +∞ и x → −∞ :

,

82

больше 1).

Опираясь на полученные данные, сделаем эскиз графика (рис. 4.2).

Рис. 4.2.

4.4.Свойства функций, непрерывных на отрезке

Первая теорема Больцано – Коши (о нуле непрерывной функции). Если функция f ( x) непрерывна на отрезке

на концах его имеет значения, противоположные по знаку, то f ( x) обращается в нуль по крайней мере в одной точке интер-

вала(a;b).

Вторая теорема Больцано – Коши (о промежуточных зна-

чениях непрерывной функции). Пусть функция f ( x) непрерыв-

на на отрезке [a;b] , причем f (a) = A , f (b) = B . Тогда, каким бы ни было число C , заключенное между числами A и B , на

83

отрезке [a;b] найдется по крайней мере одна точка c , такая, что f (c) = C.

Эти теоремы устанавливают, что, переходя от одного своего значения к другому, функция хотя бы одни раз принимает каждое свое промежуточное значение между ее значениями на концах отрезка.

Первая теорема Вейерштрасса (об ограниченности непре-

рывной на отрезке функции). Если функция f ( x) непрерывна на отрезке [a;b] , то она ограничена на нем сверху и снизу, т.е.

существуют такие числаm и M , что для всех x [a;b] спра-

ведливо неравенство m ≤ f ( x) ≤ M .

Вторая теорема Вейерштрасса (о достижении непрерывной на отрезке функции своих верхней и нижней граней). Если

функция f ( x) непрерывна на отрезке [a;b] , то она достигает на этом отрезке свои наименьшее и наибольшее значения.

Задачи

Найти и классифицировать точки разрыва:

Задачи для самостоятельного решения

Задание 14

84