Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Московский государственный университет путей сообщения

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Матан. М.В.Ишханян

.pdf

Скачиваний:

266

Добавлен:

09.06.2015

Размер:

1.39 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 45 / 185 6 7 8 9 10 11 12 13 14 15 16 17 18 > Следующая >>>

3.25. y =

3.29. y =

−

3x + 5

− 2

3.26. y =

7x + 5

3.30. y =

+ 5

5x + 6

3.27. y =

+ 5

3.28. y =

4 − x

5 + 2x

Задание 4

Используя элементарные преобразования, построить эскизы графиков функций:

	9
4.1.	y = log3
		x −1
4.2.	y = ln(2x + 1)

4.3. y = log1

2 − x

4.4. y = log2

(x − 2)3

4.5. y = log2

x + 2

4.6. y = log1

3 − 3x

4.7. y = log3

x +1

4.8.y = 2 lg (1− x)

4.9.y = lg 2 − x

4.10. y = log2 1− 2x

4.11.y = 2 + log2 (x −1)

4.12.y = 2 log9 (3x − 6)

4.13.y = ln(2x −1)

4.14.y = 1 log4 (8 − 4x) 2

4.15.y = log3 (6 − 3x)

4.16.y = log8 (4 − 4x)3

4.17.y = 2 − 3lg(x +1)

4.18.y = 1− log3 (1− 2x)

4.19. y = log1		2
			1− x
	2

4.20. y = log3 (5 − x) +1

4.21. y = log3 x − 3 9

4.22. y = log3 3x −1 9

4.23. y = log 1 (1− x) + 2

4.27. y = 1+ ln (2x − 3)

4.28. y = log2

2x −1

4.24. y = log2 (2x + 4)3

4.25. y = log1 (6 + 3x)

4.29. y = log1

2 − x

1− x

4.26. y = log

4.30. y = log2

1− 2x

Задание 5

Используя элементарные преобразования, построить эскизы графиков функций:

	π			x
5.1. y =	4	+ 2 arcsin 1	+

				4

5.2.y = π − 3arccos x + 2

5.3.y = 1+ arctg(2x +1)

	y =	π	+ arcctg				2x			+
5.4.		2									1
5.4.											1
							5
	y =	π	−	1					x	−
5.5.					arcsin						1
5.5.		2		2	arcsin						1
		2		2					2
								3x			π
5.6.	y = arccos					2 +				−	4
5.6.	y = arccos					2 +				−
								4
		1				1
5.7.	y =		arctg				+ x
5.7.	y =	2	arctg				+ x
		2				4
5.8.	y = π + arctg(x +1)

	π			x
5.9. y =	2	− 2 arcsin 1	+

				2

									1
5.10.	y =	2 arcsin x +
5.10.	y =	2 arcsin x +
		π							2
		π				1					x
5.11.	y =				−		arcsin		1+
5.11.	y =	2			−	2	arcsin		1+
		2				2					2
									x		π
5.12.	y =	2 arcsin 1+								−	2
5.12.	y =	2 arcsin 1+								−
								3
5.13.	y =		1	arcctg(1+ 2x) − π
5.13.	y =			arcctg(1+ 2x) − π
		2									8
5.14.	y = π − 2 arccos								x
5.14.	y = π − 2 arccos
		2						2

								x					π
5.15.	y = 2 arcsin 1+									+
5.15.	y = 2 arcsin 1+							2		+			2
								2					2
5.16.	y = 2arcctg(1+ 2x) − π
													2
	y =	π	−		1						+		x
5.17.						arcsin 1
5.17.		4			2	arcsin 1
		4			2								3
	y =	π	− 2 arcsin					x			−
5.18.		2											1
5.18.													1
								2
5.19.	y = π − 2arctg (1+ 2x)
		2
	y =	π	−		1						+		x
5.20.						arcsin 1
5.20.		6			2	arcsin 1
		6			2								2
5.21.	y =	3π		− 2arcctg (2x −1)
5.21.	y =			− 2arcctg (2x −1)
		2
							x					2π
5.22.	y = 2arctg 1+								−
5.22.	y = 2arctg 1+								−				3
							2						3

	1	x				π
5.23. y =		arccos		−1	−
	2		2			6

	π			2x
5.24. y =	2	− 2arctg 1	+

				3

5.25. y = π − 1 arcctg (1+ 2x)

5.26.y = − π + 1 arctg (1+ 2x)

			8		2
		π		1					x
5.27.	y =		−		arccos 1+
5.27.	y =	8	−	2	arccos 1+
		8		2					2
						x			π
5.28.	y = 2 arccos 1+						−		2
5.28.	y = 2 arccos 1+						−
						3
5.29.	y = π + 2arctg (1+ 4x)
		2
		π		1				x
	y =		−		arcsin 1+
	y =		−		arcsin 1+
5.30.		4		2				6

Глава 2. Числовые последовательности

2.1.Понятие числовой последовательности

Под числовой последовательностью a1, a2 ,…, an ,… понимается функция an = f (n) , заданная на множестве натуральных чисел.

Числа a1, a2 ,…, an ,… называют членами или элементами

последовательности, an называют общим членом последовательности.

Последовательность обозначается так: {an} или an , n . Графиком последовательности является множество точек

плоскости.
Пример 1 Даны последовательности:			(3) an = n −1
(1) an =	1	(2) an = (−1)n
	n	(2) an = (−1)n

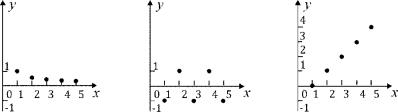
Изобразить первые пять членов на координатной плоскости. Решение Придавая n значения 1,2,3,4,5, получим:


(1)	a =		1	= 1, a		=	1	, a	=	1	, a	=	1	, a	=	1
(1)	a =			= 1, a	2	=		, a	=		, a	=		, a	=
	1	1			2	2		3	3		4	4		5	5
		1				2			3			4			5

(2)a1 = −1, a2 = 1, a3 = −1, a4 = 1, a5 = −1

(3)a1 = 0, a2 = 1, a3 = 2, a4 = 3, a5 = 4

Графики этих последовательностей изображены на рис.2.1.

Рис. 2.1.

Если для последовательности{an}справедливо неравенство an £ an+1 n , то ее называют неубывающей последовательностью.

Если для последовательности{an}справедливо неравенство an < an+1 n , то ее называют возрастающей последовательностью.

Если для последовательности{an}справедливо неравенство an ³ an+1 n , то ее называют невозрастающей последовательностью.

Если для последовательности{an}справедливо неравенство an > an+1 n , то ее называют убывающей последовательно-

стью.

Эти названия объединяют общим термином монотонная по-

следовательность.

Например, последовательность (3) из примера 1 является возрастающей.

Последовательность {an}называется ограниченной сверху , если можно указать число M , такое, что an £ M n .

Последовательность {an}называется ограниченной снизу , если можно указать число m , такое, что m £ an n .

Последовательность {an}называется ограниченной, если она ограничена и сверху, и снизу, т.е. если существуют числа m и

M , такие, что m £ an £ M n .

Геометрически это означает, что все точки, изображающие члены последовательности {an}, лежат на отрезке [m; M ] .

Например, последовательность (2) из примера 1 является ограниченной.

2.2.Предел последовательности

Введем понятие предела последовательности.

Число a называется пределом числовой последовательно-

сти {an}, если для любого, сколь угодно малого, положитель-

ного числа ε > 0 , найдется такое число N (зависящее от ε , N = N (ε ) ), что для всех членов последовательности с номе-

рами n > N верно неравенство

| an − a |< ε .

Если данное условие выполняется, то пишут lim a = a или

n→∞ n

an → a при n → ∞ .

С помощью логических символов определение предела последовательности выражается следующим образом:

lima = a ε > 0 N = N (ε ) n > N | a − a |< ε

n→∞ n n

Числовая последовательность имеет бесконечный предел, если для любого, сколь угодно большого, положительного числа ε > 0 , существует такое число N (зависящее от ε , N = N (ε ) ),

что для всех членов последовательности с номерами n > N верно неравенство | an |> ε .

Если данное условие выполняется, то пишут lim a = ∞ или

n→∞ n

an → ∞ при n → ∞ .

Последовательность, имеющая предел называется сходящей-

ся, иначе – расходящейся.

Пример 2 Используя определение предела последовательно-

сти, доказать, что lim	n + 2	=	1	. Найти номер члена последо-

n→∞ 2n +1 2				n + 2
					−	1	< 0.001
вательности, начиная с которого

				2n +1 2
45

Решение Покажем, что для произвольного сколь угодно ма-

лого действительного числа ε > 0 можно указать порядковый
номер N элемента последовательностиa =	n + 2	, начиная с
номер N элемента последовательностиa =	2n +1	, начиная с
n

которого выполняется условие

n + 2	−	1	< ε


2n +1 2

Имеем

n + 2 − (2n +1)

. Так

как n > 0 , то

4n + 2

2(2n +1)

> 0 .

4n + 2

Следовательно,

.Получаем, что

4n + 2

< ε 3 < ε (4n + 2) 4n + 2 >

4n + 2

3 − 2ε

n >

− 2

n >

4ε

	3 − 2ε
Таким образом, начиная с номера	N (ε ) =		+1(на-
		4ε

помним, что запись [x] обозначает целую часть числа. Напри-

n + 2

−

< ε . То есть

мер,

[5, 46] = 5 .) выполняется условие

2n +1 2

по

определению предела числовой

последовательности

lim

n + 2

n→∞ 2n +1 2

n + 2

−

< 0.001:

Найдем N , начиная с которого

2n +1

3 -		2 ×0.001
N (0.001) =			+1 = [749.5] +1 = 750 . То есть на-
	4
		×0.001

чиная с a750 , все члены последовательности отличаются от 1 2

менее, чем на 0.001 .

Последовательность {an } называется бесконечно малой, ес-

ли lim an = 0 .

n→∞

Последовательность {an } называется бесконечно большой,

если lim an = ¥ .

n→∞

Теорема 1. Пусть существуют конечные пределы последовательностей {xn } и { yn } .

Если порядковый номер

N , такой что n > N выпол-

няется условие xn < yn , то lim xn

£ lim yn

;

n→∞

Если порядковый номер

N , такой что n > N выпол-

няется условие xn

= C,C = const , то lim xn = C ;

( xn

± yn ) = lim xn

n→∞

lim

± lim yn ;

n→∞

lim

( xn

× yn ) = lim xn × lim yn ;

n→∞

→∞

n→∞

lim x

lim

n→∞

, где lim yn

¹ 0, yn

¹ 0 .

lim y

n→∞ y

n→∞

Теорема 2. Всякая сходящаяся числовая последовательность ограничена.

Теорема 3. Всякая монотонная ограниченная последовательность имеет предел.

Теорема 4. Числовая последовательность {an } с общим


членом a	=	1		( p > 0, p ) сходится и lim		1	= 0 .
членом a	=	n p		( p > 0, p ) сходится и lim			= 0 .
n		n p			n→+∞ n p
Теорема 5.				Если\| q \|< 1 (q ) , то последовательность с
общим членом			a = qn сходится и		lim qn = 0 .
				n	n→+∞
					n→+∞

Задачи

34.Последовательность {an } задана рекуррентным соотношением an+1 = 5an - 4, a1 = 2 . Найти пятый член этой последо-

вательности.

Написать первые десять членов последовательностей с общими членами:

35.	an		=	n	.		40.	an		=		1		.
35.	an		=		.		40.	an		=	(3n −1)(3n + 1)			.
				n + 2							(3n −1)(3n + 1)
36.	an		=	2n		.	41.	a		=	1+ (−1)n		.
				3n - 2					n		1+ (−1)n

												2
												2
37.	an		= n!.				42.	a		=	1	.
							42.	a		=		.
38.	an = -2n .								n		2n
			=	n2 −1			43.	a		= sin π n .
39.	a					.			n			2
39.	a	n		n2 + 1		.						2
		n		n2 + 1

Написать формулу общего члена последовательности по данным ее первым членам:

44.	1	,	1	,		1	,		1		,	1		,...			46.	1		,		4		,		7		,		10		,		13		,...
			6															6																26
	3			9				12			15									11				16				21
45.	1			,	1					,	1		,		1	,...	47.	3	,		7		,		11		,		15		,		19		,...
															×10			5
	3×4 5 ×6 7 ×8 9																			8 11 14 17
																	48

48.	1	,	1	,	1	,	1	,	1		,	1	,...	49.	0,	1	,	2	,	3	,	4	,	5	,... ;
48.	3	,		,	27	,		,			,	729	,...	49.	0,		,		,		,		,		,... ;
	3	9			27	81			243			729			3		4		5		6		7
Задачи для самостоятельного решения
												Задание 6*
Доказать,					что lim an					= a . Определить для каждого ε > 0 число
							n→∞

N = N (ε ) .

Заполнить таблицу:

ε 0.1 0.02 0.003

N (ε )

6.1.an

6.2.an

6.3.an

6.4.an

6.5.an

6.6.an

6.7.an

6.8.an

=	3n − 2	, a =	3
	2n −1
		2

= − 5n , a = −5
n +1
= 2n +1 , a = 2
3n − 5	3

=1− 2n , a = −2 n + 3

=3n , a = −3

2 − n

=	n	, a =	1
	3n −1
		3

=3n , a = 3 n −1

=4 + 2n , a = − 2

−3n 31

6.9. an

6.10.an

6.11.an

6.12.an

6.13.an

6.14.an

6.15.an

6.16.an

=5n +15 , a = −5

6 − n

=3 − n , a = − 1 + 2n 21

=	7n + 4	, a =	7
	2n +1
		2

=7n −1 , a = 7 n +1

=9 − n , a = − 1

+2n 21

=	1	− 2n	, a = −	1
		+ 4n
2			2

=4n −1 , a = 2

2n +1

=2n − 5 = 2

+1 , a 33n

<<< < Предыдущая 1 2 3 45 / 185 6 7 8 9 10 11 12 13 14 15 16 17 18 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
09.06.201523.18 Кб63Маржинальный анализ.docx
#
09.06.201550.34 Кб8Маркетинг лекции.docx
#
28.03.20162.5 Mб14Мастер редактирования фото и изображений.pdf
#
09.06.2015782.85 Кб32Мат.+ТКМ+Св.doc
#
09.06.2015150.17 Кб22мат.pdf
#
09.06.20151.39 Mб266Матан. М.В.Ишханян.pdf
#
09.06.2015781.97 Кб20матан.pdf
#
28.03.2016322.44 Кб19Математика КР4,5.pdf
#
19.11.20191.02 Mб5Математика новая.doc
#
09.06.20151.98 Mб285Математика ответы на билеты(1курс).docx
#
09.06.20151.05 Mб12Математика работа 1.pdf