Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Межрегианальная Академия Управления Персоналом

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Практикум з вищої математики

.pdf

Скачиваний:

Добавлен:

08.06.2015

Размер:

1.69 Mб

Скачать

☆

<<< < Предыдущая 12 / 122 3 4 5 6 7 8 9 10 11 12 > Следующая >>>

17.

∫∫x2 ydxdy; D : y =

2x − x2 , x + y = 2.

18.

∫∫(8xy + x2)dxdy; D : y =1− x2, y = − x −1.

19.

∫∫(x2 + y)dxdy;

D: y =

y = 2x, xy = 2(x ≥ 0).

20.

∫∫

dxdy; D: y =

, y =

, x =1.

D x

21.

∫∫(2x + y)dxdy;

D: y = −x2 + 2x + 3, y = 2x.

22.

∫∫(3x + 4y)dxdy;

y2 = 4x + 4, y = 2 − x.

23.

∫∫(12xy + 9x2 y2)dxdy; D: x =1, y = −x2, y =

24.

∫∫

(x + 2)

dxdy;

x + y = 2, y = x, y = 0.

25.

∫∫(2x2 + 3y2)dxdy;

D: x = 2, y = −x2, y =

Задача 2. Змініть порядок інтегрування.

412x

1. ∫dx ∫ f (x, y)dy .

03x2

412x

3. ∫dx ∫ f (x, y)dy .

03x2

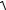
2 3− y2

5. ∫ dy ∫ f (x, y)dx .

0y2

26−x

7. ∫dx ∫ f (x, y)dy .

02x

2 4− y2

9. ∫ dy ∫ f (x, y)dx .

04y −1

21−x2

2. ∫dx ∫ f (x, y)dy .

012(1−x)2

	0				x+1		1				1− x
4.	∫ dx ∫ f (x, y)dy + ∫dx ∫ f (x, y)dy.
	−1 − x+1						0			− 1− x
							12−x
	8		2x			18	12−x
6.	∫dx ∫ f (x, y)dy + ∫ dx ∫ f (x, y)dy.
	2	4−x				8	−		2x
	3	y+4				8	10− y
8.	∫dy ∫ f (x, y)dx + ∫dy ∫ f (x, y)dx .
	0	3		y		3	3	y

310− y

10. ∫dy ∫ f (x, y)dx.

19 y

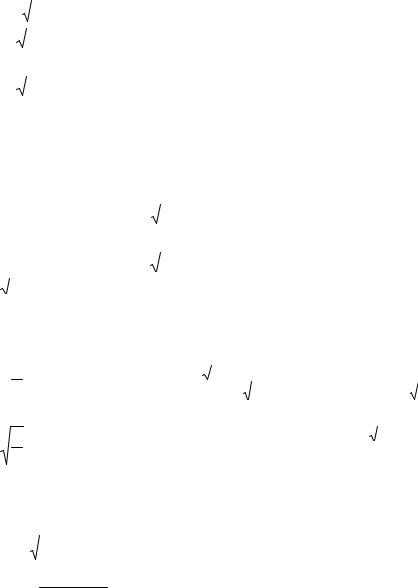
	1				1−x2					π	sin x
11.		∫ dx					∫ f (x, y)dy .		12. ∫dx ∫ f (x, y)dy.
	−1								0		0
	−1			− 1−x2					0		0
		1+
	1	1+				1− y			2		ln y
13.	∫dy				∫ f (x, y)dx .				14. ∫dy		∫ f (x, y)dx .
	0					y			1		ln	1
											ln		y
													y
	1		2− y						1/ 3		3y			81	1
15.	∫dy			∫ f (x, y)dx .					16. ∫ dy ∫ f (x, y)dx + ∫						dy ∫ f (x, y)dx.
	0			y					0			y2		1/ 3			y2
			2	y
	3				4			1+	4− y
	3		3		4			1+	4− y
17.	∫dy ∫ f (x, y)dx + ∫dy								∫ f (x, y)dx.
	0		0		3			1−	4− y
	2								1					10	1
	2			x					1		x			10	1
18. ∫dx ∫ f (x, y)dy .									19.∫dx		∫ f (x, y)dy + ∫ dx ∫ f (x, y)dy .
	0		x2						0		1		x	1	1		x
											10		x			10	x

4 y

20. ∫dy ∫ f (x, y)dx.

	2
2	2x+3
22. ∫dx	∫ f (x, y)dy .
1	2x

1	2+	7−6y− y2
24. ∫ dy		∫ f (x, y)dx .

−7 2−7−6y− y2

	2
		1− y2		0			1− y2
2		1− y2		0			1− y2
21. ∫ dy		∫ f (x, y)dx +		∫		dy	∫ f (x, y)dx.
0		y	−		2		− y
			−	2
				2

13x

23.∫dx ∫ f (x, y)dy .

02x

1	2	2	2
25. ∫	dy ∫ f (x, y)dx + ∫dy ∫ f (x, y)dx.
1/ 2	1/ y	1	y

§2. ЗАМІНА ЗМІННИХ У ПОДВІЙНОМУ ІНТЕГРАЛІ

Основні теоретичні відомості

[1] – §1, с.420-426; [2] – §1, с.574-576; [3] – глава ХІV, §5-6, с.168-178; [4] – глава VII, §2, с.271-273; [5] – глава I, §2, с.10-13.

Розглянемо подвійний інтеграл ∫∫ f (x, y)dxdy , де функція f (x, y) непе-

рервна в замкненій і обмеженій області D площини Oxy .

Нехай область D площини Oxy взаємно однозначно відображається на область D′ площини O′uv за допомогою формул x = x(u,v), y = y(u,v) , які називають формулами перетворення координат. Нехай функції x(u,v), y(u,v)

неперервні і мають неперервні частинні похідні в області D′ площини O′uv . Означення. Функціональний визначник

∂x ∂x

J (u,v) = ∂u ∂v

∂y ∂y

∂u ∂v

називають якобіаном даного відображення.

Теорема (про заміну змінних у подвійному інтегралі). Якщо J(u,v) ≠ 0 в області D′ , то має місце формула заміни змінних у подвійному інтегралі:

∫∫ f (x, y)dxdy = ∫∫ f (x(u,v), y(u,v)) J(u,v) dudv .

DD′

При переході від декартових координат (x; y) до полярних (ρ; ϕ) фор-

				x = ρ cosϕ,		а якобіан дорівнює
мули перетворення мають вигляд						а якобіан дорівнює
				y = ρ sinϕ,
	∂x ∂x		cosϕ	− ρ sinϕ
	∂x ∂x

J (u,v) =	∂ρ ∂ϕ	=			= ρ cos2 ϕ − (−ρ sin2 ϕ) = ρ .
J (u,v) =	∂ρ ∂ϕ	=			= ρ cos2 ϕ − (−ρ sin2 ϕ) = ρ .
	∂y ∂y		sinϕ	ρ cosϕ

	∂ρ ∂ϕ

Отже, має місце формула:

∫∫ f (x, y)dxdy = ∫∫ f (ρ cosϕ,ρ sinϕ)ρ dρ dϕ .

DD′

	ρ2(ϕ)		Якщо область D обмежена променями,
	ρ2(ϕ)	які утворюють з полярною віссю кути α та
	D	β	(α < β ) і кривими
ρ1(ϕ)	D
ρ1(ϕ)			ρ = ρ1(ϕ), ρ = ρ2(ϕ) (ρ1(ϕ) <ρ 2(ϕ))
β	α	(рис.3), то:
	Рис.3		β	ρ2	(ϕ)
		∫∫ f (x, y)dxdy = ∫dϕ			∫ f (ρ cos(ϕ),ρ sin(ϕ))ρdρ .
		D	α	ρ1	(ϕ)

Якщо область D охоплює початок координат, а будь-який полярний радіус перетинає границю області, яку задано рівністю ρ = ρ(ϕ), в одній то-

чці (зіркова область відносно полюса), то формула перетворення має вигляд:

	2π	ρ(ϕ)
∫∫ f (x, y)dxdy = ∫ dϕ		∫ f (ρ cos(ϕ),ρ sin(ϕ))ρdρ .
D	0	0

Питання для самоконтролю

1.Дайте означення якобіана відображення.

2.Сформулюйте теорему про заміну змінних у подвійному інтегралі.

3.Чому дорівнює якобіан у полярних координатах.

4.Як знаходяться межі інтегрування для повторного інтеграла у полярних координатах? Наведіть приклад області, для якої межі інтегрування у полярних координатах сталі.

Зразки розв’язування задач

Приклад 1. За допомогою переходу до полярних координат, обчисліть подвійний інтеграл

	∫∫	4 − (x2 + y2)dxdy,
	D
якщо область D – круг радіуса R = 2 з центром у початку координат.
Розв’язання.
y		Покладаючи x = ρ cosϕ, y = ρ sinϕ , маємо
		∫∫ 4 − (x2 + y2 )dxdy =
		D
0	2 x	= ∫∫	4 − (ρ 2 cos2 ϕ + ρ 2 sin2 ϕ)ρ dρ dϕ =
		D′
		2π	2
		= ∫ dϕ∫ 4 − ρ 2 ρdρ =

			0		0
							3
		2π	2		2π 2(4	− ρ 2)		2
= −	1			1			2		dϕ =	16π	.


	2	∫ dϕ∫ 4 − ρ 2 d(4 −ρ 2) = −		2	∫	3		0		3
	2	0	0	2	0	3				3
		0	0		0

Приклад 2. Обчисліть

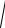∫∫x2 + y2dxdy,

якщо область D обмежена колами x2 + y2 = 2x, x2 + y2 = 4x .

Розв’язання.

Знайдемо рівняння межі області D в полярних координатах: ρ 2 cosϕ + ρ 2 sinϕ = 2ρ cosϕ ,

yx2 + y2 = 2x

x2 + y2 = 4x

звідси ρ = 2cosϕ – полярне рівняння малого кола. Аналогічно знаходимо полярне рівняння великого кола: ρ = 4cosϕ .

Отже, як видно з малюнка, якщо кут ϕ

змінюється від

−

до

, то змінна

ρ ма-

тиме межі від 2cosϕ до 4cosϕ .

Тоді маємо:

4cosϕ

∫∫

x2 + y2dxdy = ∫

dϕ

∫ ρ2dρ = ∫ dϕ ρ

∫cos3ϕ dϕ =

2cosϕ

− 2

ϕ)d

(sinϕ) =

sin3ϕ

224

∫(1− sin2

sinϕ −

− 2

Задачі для самостійного розв’язування

2.1.Обчисліть подвійні інтеграли, за допомогою переходу до полярних координат:

dxdy

а) ∫∫

, якщо область D обмежена півколом y = 1− x2

та віссю

+ y

Ox ;

б) ∫∫

sin

x2 + y

dxdy ,

якщо

область

обмежена

лініями:

+ y2

+ y

π 2

+ y

= π

;

в) ∫∫

x2 + y2dxdy ,

якщо

область

обмежена

лініями:

x2 + y2 = a2, x2 + y2 = 4a2 ;

г) ∫∫

1− x2 − y2dxdy , якщо область D – чверть круга x2 + y2 ≤1, яка знахо-

диться в першому координатному куті;

д) ∫∫

x2 + y2dxdy , якщо область D обмежена колом x2 + y2 = 2ax ;

е) ∫∫

1−

dxdy , якщо область D – круг x2

+ y2 ≤ π 2;

є) ∫∫(x2 + y2 )dxdy , якщо область D – круг x2 + y2 ≤ R2 ;

ж) ∫∫ln(x2 + y2 )dxdy , якщо область D верхнє півкільце між колами з радіу-

сами e та e2 і центром у початку координат;

з) ∫∫ydxdy , якщо область D – верхній півкруг радіуса R з центром у точці

(R;0);

і) ∫∫(x2 + y2 )dxdy , якщо область D – круг x2 + (y + 2)2 ≤ 4.

Відповіді: 2.1. а)

π ln2

;

б) 3π ; в)

14πa3

;

г)

;

д)

; е) 2π 3;

є)

πR4

; ж) πe2(3e2 −1);

з) 0; і) 48π .

Розрахункові завдання

Задача 3. Обчисліть подвійний інтеграл ∫∫dxdy по області D , що обмеже-

на заданими лініями (як буде показано у §3, такий подвійний інтеграл дорівнює площі замкненої обмеженої області D ).

y2 − 2y + x2 = 0, y2 − 4y + x2 = 0, y = x /

3, y = 3x.

2. x2 − 4x + y2 = 0, x2 −8x + y2 = 0, y = 0, y = x /

y2 − 6y + x2 = 0, y2 −8y + x2 = 0, y = x /

3, y = 3x.

4. x2 − 2x + y2 = 0, x2 − 4x + y2 = 0, y = 0, y = x.

y2 − 8y + x2 = 0, y2 −10y + x2 = 0, y = x /

3, y = 3x.

6. x2 − 4x + y2 = 0, x2 −8x + y2 = 0, y = 0, y = x.

y2 − 4y + x2 = 0, y2 − 6y + x2 = 0, y = x, x = 0.

8. x2 − 2x + y2 = 0, x2 −10x + y2 = 0, y = 0, y = 3x.

9.y2 − 6y + x2 = 0, y2 −10y + x2 = 0, y = x, x = 0.

10.x2 − 2x + y2 = 0, x2 − 4x + y2 = 0, y = x / 3, y = 3x.

11.y2 − 2y + x2 = 0, y2 − 4y + x2 = 0, y = 3x, x = 0.

12.x2 − 2x + y2 = 0, x2 − 6x + y2 = 0, y = x / 3, y = 3x.

13.y2 − 4y + x2 = 0, y2 − 6y + x2 = 0, y = 3x, x = 0.

14.x2 − 2x + y2 = 0, x2 −8x + y2 = 0, y = x / 3, y = 3x.

15.y2 − 2y + x2 = 0, y2 − 4y + x2 = 0, y = 3x, x = 0.

16.x2 − 2x + y2 = 0, x2 − 4x + y2 = 0, y = x / 3, y = 0.

17.y2 − 2y + x2 = 0, y2 −10y + x2 = 0, y = 3x, y = x / 3.

18.x2 − 2x + y2 = 0, x2 − 6x + y2 = 0, y = x / 3, y = 0.

19.y2 − 4y + x2 = 0, y2 −10y + x2 = 0, y = 3x, y = x / 3.

20.x2 − 2x + y2 = 0, x2 − 6x + y2 = 0, y = x, y = 0.

21.y2 − 2y + x2 = 0, y2 − 4y + x2 = 0, y = x, x = 0.

22.x2 − 2x + y2 = 0, x2 − 4x + y2 = 0, y = 3x, y = 0.

23.y2 − 6y + x2 = 0, y2 −8y + x2 = 0, y = x, x = 0.

24.x2 − 4x + y2 = 0, x2 −8x + y2 = 0, y = 3x, y = 0.

25.y2 − 4y + x2 = 0, y2 −8y + x2 = 0, y = x, x = 0.

§3. ЗАСТОСУВАННЯ ПОДВІЙНОГО ІНТЕГРАЛА ДО ЗАДАЧ ГЕОМЕТРІЇ ТА МЕХАНІКИ

Основні теоретичні відомості

[1] – §1, с.427-429; [2] – §1, с.577-581; [3] – глава ХІV, §4, с.166, §7-10, с.179-189; [4] – глава VII, §3-5, с.274-285; [5] – глава I, §3-6, с.14-22.

Площа плоскої фігури, яка має форму замкненої обмеженої області D площини Oxy , обчислюється за формулою:

S = ∫∫dxdy .

Об’єм циліндричного тіла, яке обмежене зверху неперервною поверхнею z = f (x, y) , знизу площиною z = 0, а по боках циліндричною поверхнею,

яка вирізає на площині Oxy область D , обчислюється за формулою:

V = ∫∫ f (x, y)dxdy .

Якщо гладка поверхня задана рівнянням z = f (x, y) , то площа поверхні

обчислюється за формулою:


S =		1		∂z 2		∂z	2
S =	∫∫	1	+		+		dxdy ,
	∫∫			∂x
	D			∂x		∂y
	D

де D – проекція даної поверхні на площину Oxy .

Якщо пластинка займає область D площини Oxy і має змінну густину γ = γ (x, y), то маса m пластинки обчислюється за формулою:

m = ∫∫γ (x, y)dxdy.

Статичні моменти пластинки відносно осей Ox та Oy :

M x = ∫∫yγ (x, y)dxdy,	M y =∫∫xγ (x, y)dxdy .
D	D

Координати центра мас пластинки визначаються формулами:

xc = M y , yc = M x . m m

Зокрема, у випадку однорідної пластинки, γ (x, y) = const , отримаємо:

			∫∫xdxdy				∫∫ydxdy
x	c	=	D	, y	c	=	D	.
x		=	∫∫dxdy	, y		=	∫∫dxdy	.
			∫∫dxdy				∫∫dxdy
			D				D

Моменти інерції пластинки відносно осей Ox та Oy : Ix = ∫∫y2γ (x, y)dxdy, I y = ∫∫x2γ (x, y)dxdy ,

D D

Момент інерції відносно початку координат :

Io = ∫∫(x2 + y2)γ (x, y)dxdy = Ix + I y .

Питання для самоконтролю

1.Наведіть формулу для обчислення площі плоскої фігури.

2.Наведіть формулу для обчислення об’єму циліндричного тіла.

3.Наведіть формулу для обчислення площі поверхні.

4.Наведіть формулу для обчислення маси, статичних моментів та моментів інерції матеріальної пластини.

Зразки розв’язування задач Приклад 1. Знайдіть площу фігури, яка обмежена лініями:

x = y 2

Розв’язання.

yx − y = 0

3x = y2 − 2y

-1 0

3 x

− 2 y , x − y = 0 .

Знайдемо ординати точок перетину даних ліній.

x = y2 − 2y, Із системи

− = 0,

x y

маємо: y1 = 0, y2 = 3.

Тоді площа даної фігури буде рівна:

	3	y
S = ∫∫dxdy = ∫dy		∫dx =
D	0	y2 −2y

3	3	3		2		y	3	3		27		27		27

= ∫(y − y2	+ 2y)dy = ∫(3y − y2 )dy =		y		−				=		−		=		(кв.од).

		2				3				2		3		6

0	0							0

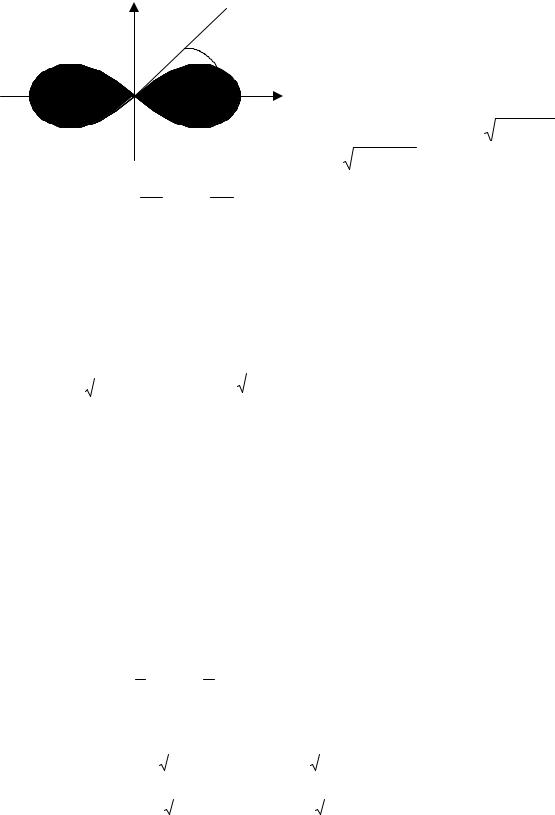
Приклад 2. За допомогою подвійного інтеграла в полярних координатах обчисліть площу фігури, що обмежена кривою, рівняння якої в декартових координатах має вигляд

(x2 + y2)2 = 2a2(x2 − y2).

Розв’язання.

Запишемо рівняння вказаної кривої в полярних координатах:

									(ρ 2 cos2 ϕ + ρ 2 sin2 ϕ)2 =
				y				π	= 2a2(ρ 2 cos2 ϕ − ρ 2 sin2 ϕ),
								π	= 2a2(ρ 2 cos2 ϕ − ρ 2 sin2 ϕ),
								4	ρ 4 = 2a2ρ 2 (cos2 ϕ − sin2 ϕ),
					0				ρ 2 = 2a2 (cos2 ϕ − sin2 ϕ),
					0			x	ρ 2 = 2a2 cos 2ϕ , ρ = a	2cos2ϕ. ρ ≥ 0 і
								x	ρ 2 = 2a2 cos 2ϕ , ρ = a	2cos2ϕ. ρ ≥ 0 і
									ρ = a 2cos 2ϕ , отже	cos2ϕ ≥ 0 , тобто
−	π	≤ ϕ ≤	π	або	3π	≤ ϕ ≤	5π	. В полярній системі координат площа області
	4		4		4		4

D обчислюється за формулою S = ∫∫ρdρdϕ . Із парності функції cos2ϕ слі-

дує, що дана фігура симетрична відносно осі Ox . Враховуючи періодичність функції cos2ϕ , маємо, що фігура симетрична також відносно осі Oy , тому

достатньо обчислити площу тієї частини фігури, яка знаходиться в першій чверті площини Oxy , і збільшити результат в 4 рази:

2cos2ϕ

2 cos2ϕ dϕ =

S = 4

∫

dϕ

∫

ρdρ = 4

∫

dϕ = 4

∫

= 4a2

4 = 2a2 (кв.од.)

∫cos2ϕdϕ = 2a2 sin 2ϕ

Приклад 3. Знайдіть об’єм тіла, обмеженого циліндром y = x2 та

площинами z = 0,

z = 2 − y .

Розв’язання.

Зробимо рисунок тіла та його проекції на площину Oxy . Областю D (проекція тіла на площинуOxy ) є параболічний сегмент, який обмежений

x2 ≤ y ≤ 2 та − 2 ≤ x ≤ 2 . Об’єм вказаного тіла шукаємо за формулою

V = ∫∫ f (x, y)dxdy .

V = ∫∫(2 − y)dxdy =

∫

dx ∫(2 − y)dy =

∫

2y −

dx =

− 2

														y			y = x2
																	y = x2
														2			y = 2
																	y = 2
														D
											− 2			0		2	x
	2	x	4	− 2x2 + 2		x	5		2	x3		2		32	2	(куб.од).
=	∫	x			dx =	x		−	2		+ 2x		=	32	2
=	∫	2			dx =	5		−	3		+ 2x		=	15
−		2				5			3			2		15
−	2										−	2
Приклад 4. Знайдіть площу частини конуса z =																x2 + y2 , яка вирі-

зана циліндром x2 + y2 − 2x = 0.

Розв’язання.

Площу заданої поверхні будемо обраховувати за відомою формулою


S =		1		∂z 2		∂z	2
S =	∫∫	1	+		+		dx dy .
	∫∫			∂x
	D			∂x		∂y
	D

Проекцію поверхні на площинуOxy (область D ) знайдемо із системи

	=		x	2	+ y	2
z	=		x		+ y		z	2 − 2x = 0 z	2 = 2x x2 + y2 = 2x.
	2			2			z	2 − 2x = 0 z	2 = 2x x2 + y2 = 2x.
	2	+ y		2	− 2x = 0
x		+ y			− 2x = 0

Маємо круг, обмежений колом x2 + y2 = 2x. У полярній системі коор-

динат ( x = ρ cosϕ , y = ρ sinϕ ) рівняння кола набуде вигляду
			ρ 2 cos2 ϕ + ρ 2 sin2 ϕ = 2ρ cosϕ ρ = 2cosϕ .
Отже −		π	≤ ϕ ≤ π	, а 0 ≤ ρ ≤ 2cosϕ .
		2	2
			z
					y
					D
			0	y	0	2 x
				y	0	2 x
x	2
x

<<< < Предыдущая 12 / 122 3 4 5 6 7 8 9 10 11 12 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
13.11.2019103.94 Кб5Практика МЭО.doc
#
04.05.20192.6 Mб3ПРАКТИКА ОД.doc
#
08.06.2015128.51 Кб6практика.doc
#
08.06.2015239.1 Кб9практика.doc
#
08.06.2015109.06 Кб21Практика_адвокат_заочка.doc
#
08.06.20151.69 Mб29Практикум з вищої математики.pdf
#
08.06.201519.22 Кб25Практическая 4.docx
#
01.07.202524.41 Кб0Практичні навички переддипломна 2014.docx
#
01.04.202538.43 Кб0практичні заняття МПП.docx
#
03.08.2019214.53 Кб2Практична робота5.doc
#
07.05.2019326.14 Кб3Практичне занятт1.doc