Практикум з вищої математики

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Межрегианальная Академия Управления Персоналом

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

а) ∫ dx ∫ f (x, y)dy ;

б) ∫dx ∫ f (x, y)dy;

в) ∫dy ∫ f (x, y)dx ;

г) ∫ dy ∫ f (x, y)dx ;

.pdf

Скачиваний:

Добавлен:

08.06.2015

Размер:

2 Мб

Скачать

☆

1 / 121 2 3 4 5 6 7 8 9 10 11 12 > Следующая >>>

М І Н І С Т Е Р С Т В О О С В І Т И І Н А У К И У К Р А Ї Н И ЧЕРКАСЬКИЙ ДЕРЖАВНИЙ ТЕХНОЛОГІЧНИЙ УНІВЕРСИТЕТ

Р. М. Дідковський Н. В. Олексієнко О. П. Грижук Н. Ю. Вовненко

ПРАКТИКУМ З ВИЩОЇ МАТЕМАТИКИ

•Кратні, криволінійні та поверхневі інтеграли

•Елементи теорії векторного поля

Черкаси 2008

МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ ЧЕРКАСЬКИЙ ДЕРЖАВНИЙ ТЕХНОЛОГІЧНИЙ УНІВЕРСИТЕТ

ПРАКТИКУМ З ВИЩОЇ МАТЕМАТИКИ

•Кратні, криволінійні та поверхневі інтеграли

•Елементи теорії векторного поля

Затверджено

на засіданні кафедри вищої математики протокол № 8 від 13.02.2008 р.

та Методичною радою ЧДТУ, протокол № __ від __.__.2008 р.

Черкаси ЧДТУ 2008

УДК 517 ББК 22.161.1

Дідковський Руслан Михайлович, к.т.н., доцент, Олексієнко Наталія Володимирівна, к.т.н., доцент, Грижук Олександра Павлівна, Вовненко Наталія Юріївна

Рецензент: Ламзіна Тетяна Борисівна, к.ф.-м.н.

Дідковський Р.М., Олексієнко Н.В., Грижук О.П., Вовненко Н.Ю. Практикум з вищої математики: Кратні, криволінійні та поверхневі інтеграли. Елементи теорії векторного поля – Черкаси: ЧДТУ, 2008. – 112 с.

Практикум містить перелік літературних джерел, короткі теоретичні відомості, питання для самоконтролю, зразки розв’язування типових завдань, задачі для самостійного розв’язування з відповідями, набори розрахункових завдань для індивідуальної роботи студентів.

Для студентів технічних спеціальностей всіх форм навчання.

УДК 517 ББК 22.161.1

Навчальне видання

ПРАКТИКУМ З ВИЩОЇ МАТЕМАТИКИ Кратні, криволінійні та поверхневі інтеграли.

Елементи теорії векторного поля

Підписано до друку __.__.2008. Формат 60х84 1/16. Папір офісн. Гарн. Times New Roman. Друк оперативний. Ум. др. арк. ___. Обл.-вид.арк. ___. Тираж ___ прим. Зам. №_____

Черкаський державний технологічний університет Свідоцтво про державну реєстрацію ДК № 896 від 16.04.2002 р. Надруковано в редакційно-видавничому центрі ЧДТУ бульвар Шевченка, 460, м. Черкаси, 18006.

ПЕРЕДМОВА

Даний посібник призначений для студентів технічних спеціальностей вищих навчальних закладів освіти, які вивчають курс вищої математики.

Посібник містить 17 параграфів, у кожному з яких подано:

•перелік літературних джерел;

•короткі теоретичні відомості;

•питання для самоконтролю;

•зразки розв’язування типових завдань;

•задачі для самостійного розв’язування з відповідями;

•набори розрахункових завдань для індивідуальної роботи студен-

тів.

Посібник може бути застосований при проведенні практичних занять та для організації самостійної роботи студентів.

Посібник рекомендовано для студентів денної форми навчання, а також може бути використаний студентами заочної форми навчання для самостійного опрацювання матеріалу.

§1. ПОНЯТТЯ ПОДВІЙНОГО ІНТЕГРАЛА ТА ЙОГО ОБЧИСЛЕННЯ

Основні теоретичні відомості

[1] – гл.VIII, §1, с.408-419; [2] – §1, с.564-569; [3] – глава ХІV, §1-3, с.152-167; [4] – глава VII, §1, с.262-270; [5] – глава I, §1, с.6-9.

Нехай функція z = f (x, D R2. Розіб’ємо область D1, D2 , …, Dn , які не мають Di позначимо Si , i =1,2,...,n Mi (xi; yi ) і утворимо суму

y) визначена в замкненій обмеженій області D сіткою довільних кривих на n частин спільних внутрішніх точок. Площі цих частин

. У кожній області Di візьмемо довільну точку

n
In = ∑ f (xi, yi ) Si,	(1)
i=1
яку назвемо інтегральною сумою функції z = f (x, y)	по області D .

Позначимо λ = max diam(Di ) – найбільший із діаметрів областей i=1,2,..,n

Di.

Означення. Якщо інтегральна сума (1) при λ → 0 має скінченну границю, яка не залежить ні від способу розбиття області D на частини Di, ні

від вибору в них точок Mi , то ця границя називається подвійним інтегралом функції f (x, y) по області D і позначається одним із символів:

∫∫ f (x, y) dS , або ∫∫ f (x, y) dxdy .

D D

При цьому область D називається областю інтегрування, а функція f (x, y)

називається інтегровною в цій області.

Теорема (достатня умова інтегровності функції). Якщо функція z = f (x, y) неперервна в замкненій обмеженій області D , то вона інтегровна

в цій області.

Деякі властивості подвійного інтеграла.

Вважатимемо підінтегральні функції інтегровними.

1. (Лінійність подвійного інтеграла.) Якщо C1 і C2 сталі числа, то

∫∫(C1 f (x, y) ± C2g(x, y)) dxdy = C1∫∫ f (x, y) dxdy ± C2 ∫∫g(x, y) dxdy.

D D D

2.(Адитивність подвійного інтеграла.) Якщо область інтегрування D функції f (x, y) розбити на області D1 і D2 , які не мають спільних внут-

рішніх точок, то

∫∫ f (x, y) dxdy = ∫∫ f (x, y) dxdy + ∫∫ f (x, y) dxdy.

D	D1	D2
3. Якщо в області D має місце нерівність		f (x, y) ≥ 0, то

∫∫ f (x, y) dxdy ≥ 0.

4. Якщо в області D f (x, y) ≥ g(x, y), то

∫∫ f (x, y)dxdy ≥ ∫∫g(x, y)dxdy .

Обчислення подвійного інтеграла.

y = y2(x)

Якщо

подвійному

інтегралі

∫∫ f (x, y)dxdy

область інтегрування

обмежена знизу і зверху двома непере-

y = y (x)

рвними кривими:

y = y1(x), y

= y2(x), y1

(x) ≤ y2(x),

а зліва і справа двома прямими x = a

та

Рис. 1

x = b (рис. 1), то

x = x1(y)

b y2 (x)

∫∫ f (x, y)dxdy = ∫

∫ f (x, y)dy dx.

(x)

a y1

У повторному інтегралі, що стоїть в цій фо-

рмулі справа, спочатку обчислюють внутрішній

інтеграл по

змінній y ,

вважаючи

величиною

x = x2(y)

сталою. Потім від одержаного результату беруть

зовнішній інтеграл по x на проміжку [a, b]. По-

Рис. 2

вторний інтеграл записують у вигляді:

y2 (x)

b y2 (x)

∫

f (x, y)dy

dx = ∫dx ∫ f (x, y)dy.

(x)

a y1(x)

a y1

Зауваження 1. Область D = {(x, y) | a ≤ x ≤ b,

y1(x) ≤ y ≤ y2(x)} назива-

ється правильною в напрямку осі Oy .

Якщо ж область D обмежена знизу і зверху, дивлячись в напрямі осі

Ox , неперервними кривими: x = x1(y),

x = x2(y),

x1(y) ≤ x2(y) , а з боків пря-

мими

y = c,

y = d , тобто

c ≤ y ≤ d

(область правильна в напрямку осі Ox )

(рис. 2), то

x2 (y)

∫∫ f (x, y)dxdy = ∫dy

∫ f (x, y)dx .

c x1(y)

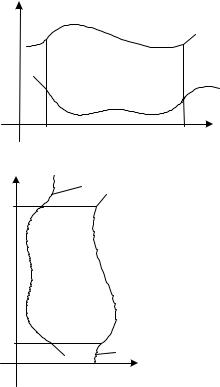
Зауваження 2. Якщо область D не є правильною ні в напрямку осі Ox ,

ні в напрямку осі Oy (тобто існують вертикальні і горизонтальні прямі, які,

проходячи через внутрішні точки області, перетинають її межу більше, ніж у

двох точках), то таку область необхідно розбити на частини, кожна з яких є

правильною областю в напрямку осі Ox чи Oy . Нехай D розбиваємо на об-

ласті D1, D2 , D3, тоді за властивістю 2 подвійного інтеграла отримаємо:

∫∫ f (x, y)dxdy = ∫∫ f (x, y)dxdy + ∫∫ f (x, y)dxdy + ∫∫ f (x, y)dxdy .

Питання для самоконтролю

1. Дайте означення подвійного інтеграла від функції f (x, y) по області D .

2. Сформулюйте достатню умову існування подвійного інтеграла.

3. Назвіть основні властивості подвійного інтеграла.

4. Дайте означення області, яка є правильною в напрямку осі Oy .

5. Дайте означення області, яка є правильною в напрямку осі Ox .

6. Сформулюйте правило розстановки меж інтегрування у повторному інтегралі.

Зразки розв’язування задач

Приклад 1. Обчисліть подвійний інтеграл

∫∫(x + y)dxdy ,

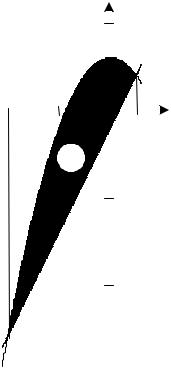
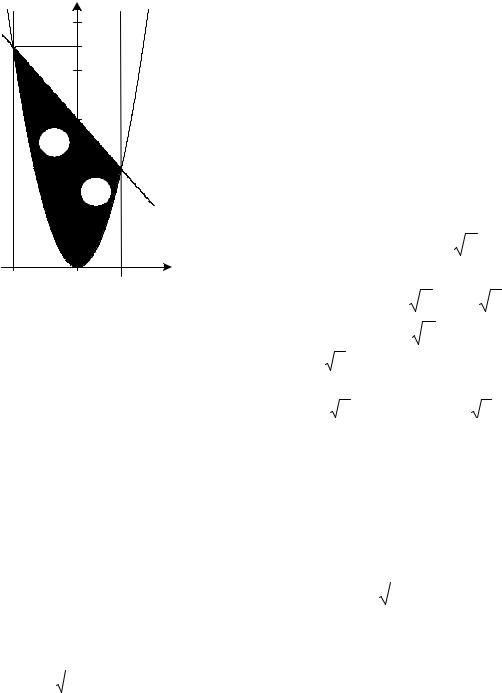
якщо область D обмежена лініями y = 3 − x2 і y = 3x −1.

Розв’язання.

Побудуємо область D . Лінія y = 3 − x2 – парабола з вершиною в точці

(0; 3),

симетрична

відносно

осі Oy і обмежує область

D зверху. Лінія

y = 3x −1 – пряма, яка обмежує область знизу.

Знайдемо координати точок перетину цих ліній:

= 3

− x

A(−4; −13),

B(1; 2).

= 3x −1;

Оскільки область

D є правильною в напрямку

осі Oy , то маємо

-4

-2

0 1 x

3−x

3−x2

∫∫(x + y)dxdy= ∫ dx

∫(x + y)dy = ∫

xy +

dx =

-5

−4 3x−1

−4

3x−1

− x2)2

−

(3x −1)2

= ∫

x(3− x2) +

− x(3x −1)

−4

-10

3x − x3

− 3x2 +

− 3x2

(3x −1)2

= ∫

+ x −

dx =

−4

x2 −

− 2x3 +

(3x −1)3

−

512

2197

−4

−

− 2 +

−

− 24 + 64 +18 +

−128 − 8 −

= −93,75.

	Приклад 2. Змініть порядок інтегрування у повторному інтегралі
					2	6−x
					∫ dx ∫ f (x, y)dy .
					−3	x2
	Розв’язання.
	10	y			Побудуємо			область	D ,	яка обмежена зліва і
	10	y			справа прямими			x = −3, x = 2		відповідно, знизу пара-
	9				справа прямими			x = −3, x = 2		відповідно, знизу пара-
	9				болою y = x2, зверху прямою y = 6 − x (рис. 2).
	8				болою y = x2, зверху прямою y = 6 − x (рис. 2).
	8				Область правильна відносно вісі Oy . Тобто
					Область правильна відносно вісі Oy . Тобто
		6				D = {(x; y) \| −3 ≤ x ≤ 2, x2 ≤ y ≤ 6 − x .
	D1				Спроектуємо область D на вісь Oy . Проекцією
	4				буде відрізок [0; 9].
	D2				Оскільки лінія, на якій містяться точки виходу з
	2				області (під час руху зліва направо), задана двома різ-
					ними рівняннями			x = 6 − y	і x =		y , то дану область
-3	0	2	x		потрібно розбити на дві частини D1 і D2. Маємо:
			x			D1 = {0 ≤ y ≤ 4; − y ≤ x ≤ y };
						D1 = {0 ≤ y ≤ 4; − y ≤ x ≤ y };
						D2 = {4 ≤ y ≤ 9; − y ≤ x ≤ 6 − y }.
			2		6− x	4		y		9	6− y
	Тому		∫	dx	∫ f (x, y)dy = ∫dy			∫ f (x, y)dx + ∫dy			∫ f (x, y)dx.
			−3		x2	0	−	y		4	− y

Задачі для самостійного розв’язування

1.1.Обчисліть повторні інтеграли:

2	3	2 + 2xy)dy;	2	y2
а) ∫dx∫(x		2 + 2xy)dy;	б) ∫dy ∫(x + 2y)dx ;
0	0		0	0
2π		a	5	5−x
	cos2 xdx∫ ydy ;
в) ∫	cos2 xdx∫ ydy ;		г) ∫dx	∫	4 + x + y	dy .
0		0	0	0

1.2.Змініть порядок інтегрування:

e	ln x				π	sin x
д) ∫dx ∫ f (x, y)dy ;					е) ∫dx ∫ f (x, y)dy
1	0				0	0
9/16				3/ 4	3/ 4
9/16			y	3/ 4	3/ 4
є)	∫ dy ∫ f (x, y)dx + ∫ dy ∫ f (x, y)dx ;
	0	y		9/16	y
2 x2				4 10−x	7 10−x

ж) ∫dx ∫ f (x, y)dy + ∫dx ∫ f (x, y)dy + ∫dx ∫ f (x, y)dy.

0 0 2 0 4 x−4

1.3.Обчисліть подвійні інтеграли по областях, що обмежені заданими лініями:

а) ∫∫(x + 2y)dxdy, D : y = x, y = 2x, x = 2, x = 3;

б) ∫∫(3x2 − 2xy + y)dxdy,D :x = 0, x = y2, y = 2;

в) ∫∫yln xdxdy,D :xy =1, y =

,x = 2;

г) ∫∫(3x + y)dxdy,D :x2 + y2 ≤ 9, y ≥ x + 3;

д) ∫∫y2 cos xydxdy, D :x = 0, y =

, y = 2x;

е) ∫∫(xy − 4x3 y3)dxdy,

D :x =1, y = x3, y = −

є) ∫∫(cos2x + sin y)dxdy, D : x = 0, y = 0, 4x + 4y − π = 0.

πa

y−1

Відповіді: 1.1. а) 17;

б) 11,2; в)

1.2. а)

∫ f (x, y)dx ;

; г) 60,4.

∫ dy

−1

−

1− y2

2− y

б) ∫dy∫ f (x, y)dx + ∫dy ∫ f (x, y)dx ;

в) ∫ dx ∫ f (x, y)dy + ∫dx∫ f (x, y)dy ;

1/ 2 1/ x

π −arcsin y

г) ∫dx ∫ f (x, y)dy + ∫dx ∫ f

(x, y)dy ; д) ∫dy ∫ f (x, y)dx ; е) ∫dy

∫ f (x, y)dx

−

e y

arcsin y

3/ 4

y+4

8 10− y

є) ∫ dx ∫ f (x, y)dy ; ж) ∫dy ∫ f (x, y)dx + ∫dy ∫ f (x, y)dx.

5(2ln2 −1)

1.3. а)

;

б) 244 ;

в)

;

г) –90; д) 1;

е) −

;

є)

+ 1− 2

Розрахункові завдання

Задача 1. Обчисліть подвійний інтеграл по області D , що обмежена заданими лініями.

1. ∫∫(x − y)dxdy; D: y = 0, y = x, x + y = 2.

∫∫

dxdy;

D: x = 2, y = x, xy =1.

D y

D: x = y2 −1, x = −1, y = 2.

∫∫e y dxdy;

∫∫(9x2 y2 + 48x3y3)dxdy; D: x =1, y =

, y = −x2.

∫∫cos(x + y)dxdy;

D : x = 0, y = π , y = x.

∫∫xdxdy; D: x = 0, y = x3, y + x = 2.

∫∫

dxdy; D: x = 0, y = x2 +1, y = 2x.

∫∫sin(x + y)dxdy;

D: y = 0, y + x = π , y = x.

∫∫x2(y − x)dxdy;

D: x = y2, y = x2.

10. ∫∫x2 y3dxdy; D:y = 0, y =1− x2.

11. ∫∫x2(y − x)dxdy;

D: y = −

, y = x2, x = 2.

12. ∫∫(x + 2y)dxdy; D : y = 3, y = −3, x = 5,x = y2 − 4.

D
13. ∫∫(x + y)dxdy;				D : y2 = 2x, x + y = 4, x + y =12.
D
14. ∫∫xydxdy; D : xy =1, x + y = 5.
D				2
D
15. ∫∫ydxdy;			D: x+ y = 2, x =		y2	−1.
15. ∫∫ydxdy;			D: x+ y = 2, x =			−1.
D				4
D
16. ∫∫		x2	dxdy;	D : x =1, y = x, y = 0.
16. ∫∫	1	+ y2	dxdy;	D : x =1, y = x, y = 0.
D	1	+ y2
D

1 / 121 2 3 4 5 6 7 8 9 10 11 12 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
13.11.2019104 Кб6Практика МЭО.doc
#
04.05.20193 Мб4ПРАКТИКА ОД.doc
#
08.06.2015109 Кб21Практика_адвокат_заочка.doc
#
08.06.2015129 Кб6практика.doc
#
08.06.2015239 Кб11практика.doc
#
08.06.20152 Мб29Практикум з вищої математики.pdf
#
08.06.201519 Кб25Практическая 4.docx
#
03.08.2019215 Кб2Практична робота5.doc
#
07.05.2019326 Кб5Практичне занятт1.doc
#
01.07.20251 Мб12Практичний посібник роботодавця с ОП.docx
#
01.07.202524 Кб1Практичні навички переддипломна 2014.docx