Практикум з вищої математики

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Межрегианальная Академия Управления Персоналом

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Частини сфери x2 + y

2 + z2 = 4, яка вирізана циліндром

Частини площини

z = x, яка

розташована всередині циліндра

x2 + y2 = 4 вище площини z = 0.

.pdf

Скачиваний:

Добавлен:

08.06.2015

Размер:

1.69 Mб

Скачать

☆

<<< < Предыдущая 1 23 / 123 4 5 6 7 8 9 10 11 12 > Следующая >>>

Із рівняння конуса маємо:
∂z =	x	,	∂z =	y	.
∂z =		,	∂z =		.
∂x	x2 + y2		∂y	x2 + y2

S = ∫∫

dxdy =

∫∫

dxdy

+ y

2cosϕ

ρ 2

2cosϕ

∫∫dxdy =

∫∫ρdρdϕ =

∫

dϕ

∫ρ dρ =

∫

dϕ =

D′

− 2

−

+ cos2ϕ

= 2

2 ∫cos2 ϕ dϕ = 2

2 ∫

dϕ =

2 ϕ

sin2ϕ

2π (кв.од.).

− 2

−

− 2

Простіші обрахунки шуканої площі можна провести враховуючи,

що∫∫dxdy

– це площа області

D , яка дорівнює

Sкруга = πR2 . R=1, тому

Sкруга = π (кв.од.). Отже,

S = ∫∫

dxdy =

Sкруга =

π (кв.од.).

∫∫dxdy =

2 + y

2 + y2

Приклад 5. Знайдіть центр ваги однорідної пластинки (γ =1), обмеженої кривою y = cosϕ, − π2 ≤ x ≤ π2 та віссю Ox .

Розв’язання.

Внаслідок симетрії пластинки відносно осі Oy маємо xc = 0. Для знаходжен-

ня yc скористаємось формулою

∫∫ydxdy

M x

. У даному випадку

∫∫dxdy

-2

2 x

≤ y ≤ cosx, −

≤ x ≤

D = 0

Обчислимо M x, m

cos x

cos2 x

M x = ∫

dx ∫

ydy = ∫

dx =

∫(1+ cos2x)dx = ∫(1+ cos2x)dx =

− 2

−

− 2

(x +

1 sin 2x)

π .

−

cos x

M x

m = ∫ dx

∫

dy = ∫ cosxdx = sin x

= 2 . Тоді yc =

−

− 2

Отже, центр ваги даної пластинки міститься в точці

Задачі для самостійного розв’язування

3.1. Обчисліть площі фігур, які обмежені заданими лініями: а) y = 2 − x, y2 = 4x + 4 ;

б) y2 = 2x, y2 = 4x − x2 (поза параболою); в) 5x2 = 9y, 3y2 = 25x ;

г) y = cos x, y = cos2x, y = 0 (площа ближньої від початку координат фігури); д) ρ = 2 − cosϕ, ρ = 2 (поза кардіоїдою);

е) ρ = 2(1+ cosϕ), ρ = 2cosϕ .

3.2. Обчисліть об’єми тіл, які обмежені заданими поверхнями: а) x2 + y2 = 8,x = 0, y = 0,z = 0,x + y + z = 4;

б) x2 + y2 = z, y = x2, y =1, z = 0;

в) z = 4 − x2,2x + y = 4,x = 0, y = 0,z = 0; г) z = 5x, x2 + y2 = 9, z = 0 ;

д) x + y + z = 6, 3x + 2y =12,3x + y = 6, y = 0, z = 0 ; е) z = x + y +1, y2 = x,x =1, y = 0, z = 0 .

3.3.Знайдіть площу частини поверхні y = x2 + z2, яка вирізана циліндром x2 + z2 =1 і розташована в першому октанті.

3.4.Знайдіть площу тієї частини площини z = x, яка розташована всередині циліндра x2 + y2 = 4 вище площини z = 0.

3.5.Обчисліть площу поверхні конуса x2 − y2 − z2 = 0, яка розташована

всередині циліндра x2 + y2 =1.

3.6. Знайдіть площу поверхні циліндра z = x2 , яка вирізана площинами x + y = 2, x = 0, y = 0.

3.7.Обчисліть площу поверхні циліндра x2 + z2 = 4 , яка розташована всередині циліндра x2 + y2 = 4.

3.8.найдіть центр ваги площі, яка обмежена параболами y2 = x, x2 = y .

3.9.Визначте координати центра ваги площадки, яка обмежена лініями y = x2, y = 2x2, x =1, x = 2.

3.10.Знайдіть центр ваги площі, яка обмежена однією петлею кривої

ρ= asin2θ .

3.11.Знайдіть центр ваги площі, яка обмежена лініями y = 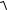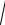2x − x2 , y = 0.


3.12. Обчисліть			момент	інерції	площі,	яка	обмежена	лініями
y = 4 − x2, y = 0, відносно осі Ox .
3.13. Обчисліть			момент	інерції	площі,	яка	обмежена	лініями

y = 2	x	,x + y = 3, y = 0, відносно осі Ox .

3.14.Обчисліть масу круглої пластинки радіуса R , якщо її густина обернено пропорційна віддалі точки від центра і рівна δ на краю пластинки.

Відповіді: 3.1. а)																			64		;			б) 2π −											16		;		в) 5;				г) 1		; д) 8 − π ;									е)5π .
																		3															3
																																										2
3.2. а)8π −								32 2							; б)					88			; в)					40			;				г)90;					д)12; е)					19			.
							3																																						60
																		105				3
3.3. π (5						5	−1) .								3.4.2π											. 5.π .													5	+			2	ln(3 + 2								).
																							2										3.6.																		2			3.7. 32.
																																						6				2
					24
3.8.		=			9		,					=			9		.	3.9.								=	45			,						=		279			.	3.10.					=			=			128a		.
	x									y														x										y												x			y
					20									20
																						28																70														105π
3.11.				=1,							=		4			.		3.12.							4096				.			3.13. 2,4.										3.14. 2πR2δ .
			x						y
													3π												105

Розрахункові завдання

Задача 4. Перейшовши до полярних або еліптичних координат, обчисліть площі плоских фігур, які обмежені заданими кривими (параметр a > 0).

1.(x2 + y2 )2 = 2ax3.	2. (x2 + y2 )2 = a(x3 − 3xy2).
3. (x2 + y2 )2 = 4ay3.	4. (x2 + y2 )3 = 4a2x2 y2 .
5. (x2 + y2 )2 = a(x3 + y3) .	6. (x2 + y2 )2 = a2(x2 − y2).
7. (x2 + y2 )2 = ax2 y .	8. (x2 + y2 )2 = 2a2xy .
9. (x2 + y2 )3 = 4x2 y2.	10 (x2 + y2 )3 = 2x5.
11. x4 + y4 = a2(x2 + y2)3.	12. y6 = a2(y4 − x4).

13. x6 = a2(x4 − y4).				14. x6 = 4(x4 − y4) .
15.(x2 + y2 )2 = 2ay3.				16.(x2 + y2 )3 = 6x2 y2 .
17.	(x2	+ y2 )2	= xy2.	18.	(x2	+ y2 )2 = 2a2 y3.
19.	(x2	+ y2 )2	=16(x2 − y2).	20.	(x2	+ y2 )3 = 2a2x2 y2 .
21.	(x2	+ y2 )3 = 9x5.		22.	y6 = 4a2(y4 − x4) .
23.	(x2	+ y2 )2	= 4xy2 .	24.	(x2	+ y2 )3 = a2x2 y2 .

25. x4 + y4 = 9(x2 + y2)3.

Задача 5. Обчисліть площі вказаних поверхонь.

1.Частини сфери x2 + y2 + z2 =16, яка вирізана циліндром x2 + y2 = 4.

2. Частини конуса y2 = x2 + z2, яка вирізана циліндром x2 + z2 = 2z .

3.Частини сфери x2 + y2 + z2 = R2 , яка вирізана циліндром x2 + z2 = Rz .

4.	Частини	сфери	x2 + y2 + z2 = 9, яка		вирізана	циліндром	x2 + y2 = 3
	(всередині циліндра).
5.	Частини	сфери	x2 + y2 + z2 =100	,	яка	обмежена	площинами
	x = −8, x = 6.
6.	Частини конуса y2 + z2 = x2, яку відсікає циліндр x2 = 2py.

7.Частини сфери x2 + y2 + z2 =1, яка вирізана циліндром x2 + y2 = 14 (всередині циліндра).

8.Частини параболоїда y = x2 + z2, яка вирізана циліндром x2 + z2 =1 і розташована в першому октанті.

9.Частини конуса y2 + x2 = z2, яка розташована над площиною Oxy і від-

	різана площиною z =					x		+
						x
					2				1 .
					2		2		1 .
							2
10.	Частини параболоїда 2z = x2 + y2, яка вирізана циліндром x2 + y2 =1 .
11.	Частини конуса z2 = 2xy , яка вирізана площинами									z = 0,x =1, y = 4.
12.	Частини	циліндра	x2 + z2 = 4 , яка розташована							всередині циліндра
	x2 + y2 = 4.
				z = x2 ,
13.	Частини	циліндра		z = x2 ,					яка вирізана площинами x + y =		2	,
	x = 0, y = 0.

14.Частини параболоїда y = x2 + z2, яка вирізана циліндром x2 + z2 =1 і розташована в першому октанті.

17.Частини параболоїда ay = x2 + z2 , яка розташована в першому октанті і обмежена площиною y = 2a (a > 0) .

18.	Частини циліндра x2 + y2 =16 (z ≥ 0) , яка розташована між площинами
	z = 4x, z = 2x.
19.	Частини конуса	x2 + y2 − z2 = 0, яка розташована всередині циліндра
	x2 + y2 =1.
	Частини сфери x2 + y2 + z2 = 4, яка обмежена площинами x = 0, x =													.
20.													2	.
21.	Частини конуса x	2	+ z	2	= y	2	, яка вирізана параболоїдом y = x		2	+	z2	.
21.	Частини конуса x		+ z		= y		, яка вирізана параболоїдом y = x			+	4	.
											4
22.	Частини конуса x2 + z2 = y2, яка вирізана циліндром y2 = 4x .
23.	Частини сфери		x2 + y2 + z2 = 8, розташованої					всередині			конуса
	x2 + y2 = z2.

24.Частини площини x + y + z = 3, яка вирізана циліндром y2 = 3x та площиною x = 3.

25.Частини параболоїда z = x2 + y2, яка вирізана циліндром x2 + y2 = 9.

	Задача 6. Знайдіть масу пластинки D , яка обмежена заданими кривими і
	має поверхневу густину γ .
1.	D :x = 1, y = 0, y2 = 4x(y ≥ 0); γ = 7x2 + y.
2.	D :x = 0, y = 0, x2 + y2 = 1, x2 + y2 = 4 (x ≥ 0, y ≥ 0); γ = 7x2 + y.
3.	D :x = 1, y = 0, y2 = 4x(y ≥ 0); γ = 7x2 / 2 + 5y.
4.	D :x = 0, y = 0, x2 + y2 = 9, x2 + y2 = 16 (x ≥ 0, y ≥ 0); γ = (2x + 5y) /(x2 + y2 ).
5.	D :x = 2, y = 0, y2 = 2x(y ≥ 0); γ = 7x2 /8+ 2y.
6.	D :x = 0, y = 0, x2 + y2 = 1, x2 + y2 = 16 (x ≥ 0, y ≥ 0); γ = (x + y)/(x2 + y2 ).
7.	D :x = 2, y = 0, y2 = x / 2(y ≥ 0); γ = 7x2 / 2 + 6y.
8.	D :x = 0, y = 0, x2 + y2 = 4, x2 + y2 = 25 (x ≥ 0, y ≤ 0); γ = (2x − 3y)/(x2 + y2 ).
9.	D :x = 1, y = 0, y2 = 4x (y ≥ 0); γ = x + 3y2.

10.	D :x = 0, y = 0, x2 + y2 = 1, x2 + y2 = 9 (x ≥ 0, y ≤ 0); γ = (x − y)/(x2 + y2 ).
11.	D :x = 1, y = 0, y2 = x (y ≥ 0); γ = 3x + 6y2.

12. D :x = 0, y = 0, x2 + y2	= 9, x2 + y2	= 25 (x ≤ 0, y ≥ 0); γ = (2y − x) /(x2 + y2 ).
13. D :x = 2, y = 0, y2 = x / 2 (y ≥ 0); γ = 2x + 3y2.
14. D :x = 0, y = 0, x2 + y2	= 4, x2 + y2	= 16 (x ≤ 0, y ≥ 0);γ = (2y − 3x) /(x2 + y2 ).

15.D :x = 1/ 2, y = 0, y2 = 8x (y ≥ 0); γ = 7x + 3y2.

16.D :x = 0, y = 0, x2 + y2 = 9, x2 + y2 = 16 (x ≤ 0, y ≥ 0);γ = (2y − 5x) /(x2 + y2 ).

17.D :x = 1, y = 0, y2 = 4x (y ≥ 0); γ = 7x2 + 2y.

18.D :x = 0, y = 0, x2 + y2 = 1, x2 + y2 = 16 (x ≥ 0, y ≥ 0);γ = (x + 3y) /(x2 + y2 ).

19.D :x = 2, y = 0, y2 = 2x (y ≥ 0); γ = 7x2 / 4 + y / 2.

20.	D :x = 0, y = 0, x2	+ y2 = 1, x2 + y2 = 4 (x ≥ 0, y ≥ 0);γ = (x + 2y) /(x2 + y2 ).
21.	D :x = 1/ 4, y = 0, y2 = 16x (y ≥ 0); γ = 16x + 9y2 / 2.
22.	D :x = 0, y = 0, x2 + y2 = 1, x2 + y2 = 9 (x ≥ 0, y ≤ 0);γ = (2x − y) /(x2 + y2 ).
23.	D :x = 2, y = 0, y2 = x / 2 (y ≥ 0); γ = 7x2 / 2 + 8y.
24.	D :x = 0, y = 0, x2	+ y2 = 1, x2 + y2 = 25 (x ≥ 0, y ≤ 0);γ = (x − 4y) /(x2 + y2 ).
25.	D :x = 1, y = 0, y2	= 4x (y ≥ 0); γ = 6x + 3y2.

§4. ПОНЯТТЯ ПОТРІЙНОГО ІНТЕГРАЛА ТА ЙОГО ОБЧИСЛЕННЯ

Основні теоретичні відомості

[1] – гл.VIII,§1,с.429-440; [2] – гл.10,§1, с.585-587; [3] – глава ХІV, §1-3, с.190-196; [4] –глава VII, §1,с.286-293; [5] - глава I, §1,с.23-28.

Нехай функція u = f (x, y,z) визначена в замкненій обмеженій області G R3. Розіб’ємо область G сіткою поверхонь на n частин Gi , які не мають

спільних внутрішніх точок і об’єми яких дорівнюють			Vi , i =1,2,...,n. У ко-
жній області Gi	візьмемо довільну точку Mi (xi; yi;zi ) і утворимо суму
	n
	In = ∑ f (xi, yi,zi )	Vi ,	(2)
	i=1
яку назвемо інтегральною сумою для функції		f (x, y,z)	по області G .
Нехай λ =	max diam(Gi ) – найбільший з діаметрів областей Gi .
	i=1,2,..,n

Означення. Якщо інтегральна сума (2) при λ → 0 має скінченну границю, яка не залежить ні від способу розбиття області G на частинні області Gi , ні від вибору точок Pi в них, то ця границя називається потрійним інтег-

ралом і позначається одним із таких символів:

∫∫∫ f (x, y,z) dV , або ∫∫∫ f (x, y,z) dxdydz.

G G

Теорема (достатня умова інтегрованості функції). Якщо функція f (x, y, z) неперервна в замкнутій обмеженій області G , то вона інтегрова-

на в цій області.

Основні властивості потрійного інтеграла

1.(Лінійність потрійного інтеграла.) Якщо C1 і C2 сталі числа, то

∫∫∫(C1 f (x, y,z) ± C2ϕ(x, y,z))dV = C1∫∫∫ f (x, y,z) dV ± C2 ∫∫∫ϕ(x, y,z) dV.

G G G

2. (Адитивність потрійного інтеграла.) Якщо область інтегрування G функції f (x, y,z) розбити на частини G1 і G2, які не мають спільних внутрі-

шніх точок, то

∫∫∫ f (x, y, z) dV = ∫∫∫ f (x, y,z) dV + ∫∫∫ f (x, y,z) dV.

3. Якщо в області G має місце нерівність f (x, y, z) ≥ 0, то і

∫∫∫ f (x, y, z)dxdydz ≥ 0.

4. Якщо в області D f (x, y, z) ≥ g(x, y, z) , то і

∫∫∫ f (x, y, z)dxdydz ≥ ∫∫∫g(x, y, z)dxdydz.

G G

Обчислення потрійного інтеграла

Якщо область інтегрування G така, що її проекція на площину Oxy область D , правильна в напрямку осі Oy , а всяка пряма, що проходить через

внутрішню точку області D паралельно осі Oz перетинає границю області G рівно в двох точках, які лежать на поверхнях z = z1(x, y), z = z2(x, y) (рис.4),

то:

		z2 (x, y)	b y2 (x)		z2 (x, y)
∫∫∫ f (x, y, z)dxdydz = ∫∫dxdy		∫ f (x, y, z)dz = ∫dx		∫ dy	∫ f (x, y, z)dz.
G	D	z1(x, y)	a y1(x)		z1(x, y)
	z		z=z2(x,y)		У	цій	формулі
	z		z=z2(x,y)	спочатку		обчислюється
				спочатку		обчислюється
				інтеграл		по	змінній z
				при умові, що x, y –
				сталі	величини, після
			z=z1(x,y)	чого отримують подвій-
			z=z1(x,y)	ний інтеграл по змінних
				y і x .
	O
	a		y
	a
	y=y1(x)
b			y=y2(x)
x	Рис. 4
	Рис. 4

Питання для самоконтролю

1.Дайте означення потрійного інтеграла функції f (x, y, z) по області G .

2.Сформулюйте достатню умову інтегрованості функції.

3.Назвіть основні властивості потрійного інтеграла.

4.Сформулюйте правило розстановки меж інтегрування у повторному інтегралі.

Зразки розв’язування задач

Приклад 1. Обчисліть ∫∫∫xdxdydz, якщо область G обмежена пло-

щинами x = 0, y = 0, z = 0, y = 3, x + z = 2.

Розв’язання.

Область G проектується на площину

	z					Oxy	у прямокутник D = {0 ≤ x ≤ 2; 0 ≤ y ≤ 3}.
						Oxy	у прямокутник D = {0 ≤ x ≤ 2; 0 ≤ y ≤ 3}.
						Оскільки			z1 = 0 (вхід),								z2 = 2 − x						(вихід), то
						маємо
										2			3			2−x
				3	y	∫∫∫xdxdydz = ∫dx∫dy										∫xdz =
				3	y	G				0			0			0
2								2		3				2− x				2			3
2								= ∫xdx∫						2− x
								= ∫xdx∫				z		0		dy = ∫xdx∫(2 − x)dy =
x								0		0								0			0
x

2					2										3		2
2			3		2		2				2			x	3		2				8
								)dx =3 x

= ∫	x (2	− x) y		dx =3∫(2x − x									−				=	3	4	−			= 4.
0			0		0									3								3
			0
																	0
																	0

Приклад 2. Обчисліть ∫∫∫ycos(z + x)dxdydz , якщо область G обме-

жена циліндром y = x та площинами y = 0, z = 0, x + z = π2 .

Розв’язання.

y = x

π	G	O		D
π		O	O	π
2		y	O	π	x
					x
x				2

Область		0	≤ x ≤	π	; 0	≤ y ≤		є проекцією просторової об-

	D = (x, y)			2			x

ласті G на площину Oxy . У напрямку осі Oz область G обмежена площинами z = 0 та x + z = π2 . Тому 0 ≤ z ≤ π2 − x . Тоді маємо:

										π								π		− x
										2					x			2		− x
										2					x			2
∫∫∫ycos(z + x)dxdydz = ∫ dx														∫ dy						∫ ycos(z + x)dz =
G										0			0						0
	π											π			−x					π
	2											π								2
					x	(ysin(z + x))							2											x					π
					x								2											x					π
= ∫dx ∫																	dy = ∫dx ∫ (ysin												2	− x + x				− ysin x)dy =
	0			0										0						0			0						2
	0			0										0						0			0
	π															π															π
	2																2		2												2
	2				x												2	y	2			sin x							x		2	x				x
= ∫dx ∫						(y − ysin x)dy								= ∫				y			−	sin x					2				= ∫	x		−		x				=
																										y				dx							sin x dx
																		2					2			y				dx			2		2		sin x dx
	0			0														2					2					0			0		2		2
	0			0													0											0			0
			π							π
		1	2					1		2							u = x										du = dx					=
			2							2
=			∫xdx −							∫xsin xdx				=
=	2		∫xdx −				2			∫xsin xdx				=													v = −cos x
	2		0				2			0							dv = sin x										v = −cos x
			0	π						0	π				π																π
				π							π				π																π
			2	2		1					2			2											π 2			1			2		π	2			1		π 2 − 8

		x
		x
=					−				− xcos x				+ ∫cos xdx										=				−		sin x		=				−			=			.
=	4				−	2			− xcos x				+ ∫cos xdx										=		16		−	2	sin x		=		16		−		2	=	16		.
	4			0		2					0			0											16			2			0		16				2		16
				0							0																				0

Задачі для самостійного розв’язування

1 2 3

4.1.Обчисліть повторний інтеграл∫dx∫dy∫dz .

0 0 0 a x y

4.2.Обчисліть повторний інтеграл ∫dx∫dy∫xyzdz.

				0	0	0
4.3.	Обчисліть	∫∫∫	dxdydz	, якщо G : x = 0, y = 0, x + y + z =1, z = 0.


		G (x + y + z +1)3
4.4.	Обчисліть	∫∫∫ x2dxdydz, якщо G обмежена площинами: x = 0, y = 0,
		G
	z = 0, x + y + z − 2 = 0 .

4.5.	Обчисліть ∫∫∫ xyzdxdydz, якщо G обмежена сферою x2 + y2 + z2 =1
				G
	та площинами: x = 0, y = 0, z = 0.
4.6.	Обчисліть			∫∫∫ ycos(z + x)dxdydz ,	якщо	G обмежена	циліндром
				G
	y =		та площинами y = 0, x + z = π , z = 0.
	y =	x	та площинами y = 0, x + z = π , z = 0.
					2
4.7.	Обчисліть ∫∫∫ xdxdydz, якщо G обмежена поверхнею z = x2 + y2 та
				G
	площиною z =1.
4.8.	Обчисліть			∫∫∫ z(x + y +1)dxdydz,	якщо G	обмежена	циліндром
				G
	x2 + z2 =1 та площинами y = 0, y =1, y ≥ 0 .
4.9.	Обчисліть ∫∫∫ xydxdydz , якщо G обмежена гіперболічним параболої-
				G
	дом z = xy та площинами z = 0, x + y =1 .

4.10. Обчисліть ∫∫∫ xy2z3dxdydz, якщо G обмежена гіперболічним парабо-

лоїдом z = xy та площинами z = 0, y = x, x =1 .
Відповіді. 4.1. 6. 4.2. a6 / 48. 4.3.					1	ln 2 −		5	. 4.4.		8	. 4.5.	1	. 4.6.	π 2	−	1	.
Відповіді. 4.1. 6. 4.2. a6 / 48. 4.3.					2	ln 2 −	16		. 4.4.	15		. 4.5.	48	. 4.6.	16	−	2	.
					2		16			15			48		16		2
4.7. 0. 4.8. 2. 4.9.	19	. 4.10.	1	.
4.7. 0. 4.8. 2. 4.9.		. 4.10.	364	.
180			364

Розрахункові завдання

Задача 7. Обчисліть потрійний інтеграл, якщо область G обмежена вказаними поверхнями.

∫∫∫ xy2z3dxdydz;

G : z = xy, y = x, x =1,

z = 0.

∫∫∫

dxdydz

;

G : x = 0,

x =1, y = 0,

y =1, z =1, z = 0.

x + y + z

∫∫∫

dxdydz

; G :

=1, x = 0, y = 0, z = 0.

G 1+

3 5 7

∫∫∫ ydxdydz;

G : y2 = 2x, x + 2y + 3z = 6, y = 0, z = 0.

<<< < Предыдущая 1 23 / 123 4 5 6 7 8 9 10 11 12 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
13.11.2019103.94 Кб2Практика МЭО.doc
#
04.05.20192.6 Mб2ПРАКТИКА ОД.doc
#
08.06.2015128.51 Кб6практика.doc
#
08.06.2015239.1 Кб9практика.doc
#
08.06.2015109.06 Кб20Практика_адвокат_заочка.doc
#
08.06.20151.69 Mб22Практикум з вищої математики.pdf
#
08.06.201519.22 Кб25Практическая 4.docx
#
03.08.2019214.53 Кб2Практична робота5.doc
#
07.05.2019326.14 Кб2Практичне занятт1.doc
#
08.06.201533.86 Кб85ПРИВАТНИЙ ВИЩИЙ НАВЧАЛЬНИЙ ЗАКЛАД.docx
#
11.11.2019264.7 Кб3программа по налоговой системе.doc