Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Межрегианальная Академия Управления Персоналом

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Практикум з вищої математики

.pdf

Скачиваний:

Добавлен:

08.06.2015

Размер:

1.69 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 56 / 126 7 8 9 10 11 12 > Следующая >>>

			Зразки розв’язування задач

Приклад 1. Знайти масу дуги кривої y =				2x x	від точки O(0; 0) до

			3
точки A	4;	16	, якщо лінійна густина в точці M кривої дорівнює довжині

		3

частини дуги OM .

Розв’язання.

Крива задана в декартовій системі координат:

y = 2x x = 2 x2 , 0 ≤ x ≤ 4 .

Знайдемо довжину частини дуги OM . Спочатку визначимо похідну

		1
y′ =	2		3

				x2 =	x	.

3		2

Тоді

ρ (M )= lOM = ∫x

d x = ∫x(1+ x)1/ 2d x = (1+ x)3/ 2

x =

−

1+ (

(1+ x)3

3/2

m = ∫ρ (x, y)dl =

4∫((1+ x)3/ 2 −1)

dx =

4∫((1+ x)2 − (1+ x)1/ 2 )dx =

1+ x

(1+ x)3

(1+ x)3/ 2

254 − 30

−

53/ 2 −

−

3/2

Приклад 2. Знайти координати центра мас дуги циклоїди

x = t − sint,

y =1− cost

(0 ≤ t ≤ π ).

Розв’язання.

Скористаємося формулами

∫x ρ (x, y) dl

M y

∫ y ρ (x, y) dl

;

∫ρ (x, y) dl

Оскільки дуга однорідна, то приймаємо ρ (x, y)=1. Тоді

m = ∫dl = ∫

(x′(t))2 + (y′(t))2dt = ∫

(1− cost)2 + sin2 t dt = ∫

2 − 2cost

dt =

= 2∫sin

dt = −4cos

= 4.

xc =		1	∫xdl =				1			π	(t − sint) 2sin												t		dt =		1	π									t		− sin			t					=
										∫																			∫			tsin												sint dt
		4					4			∫																	2		∫			tsin				2								sint dt
		4	L				4			0											2						2	0								2				2
			L							0																		0
	u = t;							du = dt												1										t			π		π								t		π			t		t



=				t												t		=					− 2tcos												− ∫− 2cos										dt − 2	∫sin2			cos		dt	=
=				t												t		=					− 2tcos												− ∫− 2cos										dt − 2	∫sin2			cos		dt	=
	dv = sin				;				v = −2cos									2										2												2								2	2
	dv = sin				;				v = −2cos									2										2												2								2	2
			2												2																		0		0											0
=	1		− 2tcos				t			+ 4sin				t	+		4		sin3					t		π					1					4				8
	1						t							t			4							t		π					1					4				8
																											=								4 +				=		.
																											=								4 +				=		.
	2						2						2 3											2		0					2					3				3
		1					1			π													t				1				π					t						t
yc =			∫ ydl =							∫(1− cos t)2sin															dt =						∫			sin				− sin						cos t dt =
yc =		4	∫ ydl =				4			∫(1− cos t)2sin													2		dt =		2				∫			sin		2		− sin						cos t dt =
		4	L				4			0													2				2				0					2				2
			L							0																					0
=	1		− 2cos			t			+		1		3t			− cos						t			π		4
	1					t					1		3t									t			π		4
												cos													=			.
												cos													=			.
	2		2								3		2								2				0		3

	Задачі для самостійного розв’язування
8.1.	Знайдіть масу відрізка лінії y = ln x між точками з абсцисами x1 і
	x2 , якщо густина лінії в кожній точці дорівнює квадрату абсциси
	точки.
8.2.	Знайдіть масу відрізка ланцюгової лінії y = ach	x	між точками з аб-

		a

сцисами x1 = 0 і x2 = a, якщо густина лінії в кожній точці обернено пропорційна ординаті точки, причому густина в точці (0;a) дорівнює S.

8.3.Знайдіть масу чверті еліпса x = acost, y = bsint , розташованої в першій чверті, якщо густина в кожній точці дорівнює ординаті цієї то-

чки.
8.4. Знайдіть	масу	першого	витка	гвинтової	лінії
x = acost,	y = asint, z = bt, густина		якої в	кожній точці	дорівнює

квадрату полярного радіуса цієї точки.

8.5.Знайдіть масу дуги лінії x = et cost, y = et sint, z = et від точки, що

відповідає t = 0, до довільної точки, якщо густина дуги обернено пропорційна квадрату полярного радиуса і в точці (1, 0,1) дорівнює

одиниці.

8.6.Знайдіть координати центра маси першого піввитка гвинтової лінії x = acost, y = asint, z = bt, якщо густина постійна.

8.7.Обчисліть статичні моменти першого витка конічної гвинтової лінії x = tcost, y = tsint, z = t , відносно площини Oxy , якщо густина про-

порційна квадрату відстані від цієї площини: S = kz2.

8.8.Обчисліть моменти інерції відносно координатних осей першого ви-

тка гвинтової лінії x = acost, y = asint, z = 2π t , якщо густина стала.

8.9.Обчислити площу частини циліндричної поверхні x2 + y2 = R2 , розміщеної між площиною Oxy і поверхнею z = k + x2 .

														k
8.10. Знайти	довжину				дуги			кривої			x = 3t, y = 3t2, z = 2t2 від точки
O(0;0;0) до A(3;3;2).
					3			3					2
Відповіді: 8.1.	1	(x2	2	+1)			− (x12 +1)			.	8.2. Sa. 8.3.	b		+	ab	arcsinε,
	1		2			2			2			b			ab		де
						2			2								де
	3										2				2ε

8π

ε – ексцентриситет еліпса. 8.4.

2πa2 +

8.6. 0;

;

. 8.7.

(3π 2

−1)(2π 2 +1)2

bπ

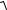a2 + b2 . 8.5. (1− e−t )3.

+1 .

8.8. J

= J

4π 2a2

+ h2 , J

= a2

4π 2a2

+ h2 .

8.9. 3πR2 .

8.10. 5.

Розрахункові завдання

Задача 12. Знайдіть масу дуг.

Півкола x2 + y2 =1,

y ≥ 0, якщо густина його в точці (x, y) дорівнює y.

−

Ланцюгової

лінії

y =

+ e

між точками

з абсцисами x = 0 і

2 

x = a, якщо густина кривої обернено пропорційна ординаті точки.

3. Кривої y = a ch x від точки A(0;a) до точки B(b;k), якщо густина маси a

в кожній точці дуги дорівнює 1.

4.Кривої y = ln x між точками з абсцисами x = 2 і x = 5, якщо лінійна густина кривої в кожній точці дорівнює квадрату абсциси точки.

5. Параболи y2 = 4x (0 ≤ x ≤1), якщо лінійна густина параболи в точці

(x, y) дорівнює y .

	y =	x2			1		(2;2), якщо лінійна
6. Параболи			,	що лежить між точками 1;		і
6. Параболи			,	що лежить між точками 1;		і
		2			2

густина дорівнює y . x

7. Кривої y =1− lncos x між точками з абсцисами x = 0 і x = π , якщо гус-

						4
тина маси в кожній точці кривої дорівнює 1.
8. Кривої y = ln	ex +1		= a	до x		= b (a< b), якщо густина маси в ко-
		від x			2

	1
	ex −1

жній точці кривої дорівнює 1.

9.Кривої 3y2 = x (x −1)2 між точками перетину з віссю Ox , якщо лінійна густина дорівнює 12 x2.

	1	x			− ln x +
10. Кривої y =			x	2 −1		x	2 −1	від x = 1 до x = a +1 (a > 0),

2

якщо лінійна густина дорівнює 3(x2 +1).

11.Параболи y = 2x2 від точки (1;1) до точки (2;8), якщо лінійна густина

дорівнює y . x

12.Параболи y2 = 2x, що лежить між точками (1;2) і (2;2), якщо лінійна

густина ρ (x, y)= x . y

	Напівкубічної параболи y2 =							4	x3, від		точки (3;2			) до точки
13.								4					3
13.													3
					9
		8;	32		, якщо лінійна густина ρ (x, y)=					x		.
			32	2						x
				2
		3									y
14.	Косинусоїди y = 2cos					x	між точками з абсцисами x = 0 і x = π , якщо лі-
14.	Косинусоїди y = 2cos						між точками з абсцисами x = 0 і x = π , якщо лі-
					2					2

нійна густина ρ (x, y)= y.

15.Кривої y =1− ln(x2 −1)між точками з абсцисами x = 3 і x = 4, якщо густина кривої в кожній точці дорівнює квадрату абсциси точки.

16. Кривої y = x3/ 2 від точок з абсцисами x = 0 і x = 4, якщо лінійна густина ρ (x, y)= 2y2 .

x
17. Кривої y = aln		a2	(0 ≤ x ≤ b < a), якщо лінійна густина кривої в ко-
	a	2 − x2

жній точці прямо пропорційна абсцисі точки.

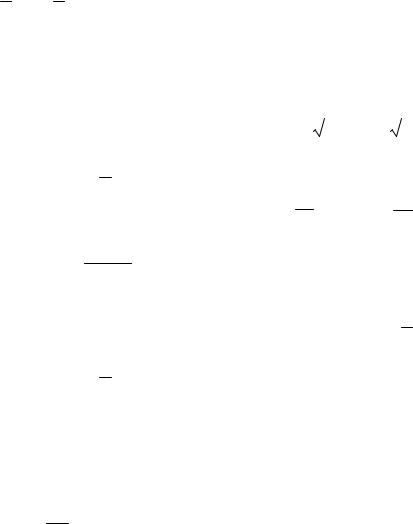
18. Кривої y = 1 x2 − 1 ln x між точками з абсцисами x = 1 і x = e, якщо лі-

нійна густина ρ (x, y)= xy.

19.	Кривої y = ex між точками з абсцисами x = 0 і x =1, якщо лінійна гус-
	тина ρ (x, y)= y.
	Параболи y =	1	x2 між точками з абсцисами x =		і x =
20.				2		3, якщо лі-

	2

нійна густина ρ (x, y)= x . y

21.Кривої y = ex між точками з абсцисами x = ln 15 і x = ln 24, якщо лінійна густина ρ (x, y)= y .

22.Кривої y = arcsin x − 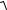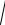1− x2 між точками з абсцисами x = 0 і x =1, якщо лінійна густина ρ (x, y)= x .

23.Параболи y = 4 − x2 між точками з абсцисами x = −1 і x = 2, якщо лі-

нійна густина ρ (x, y)= x . y

24.Кривої y2 = (x −1)3 між точками з абсцисами x = 1 і x = 3, якщо лінійна густина ρ (x, y)= xy2/3.

25.Гіперболи xy = 4 між точками з абсцисами x = 1 і x = 4, якщо лінійна

густина ρ (x, y)= x2 . y3

§9. КРИВОЛІНІЙНІ ІНТЕГРАЛИ IІ РОДУ (ПО КООРДИНАТАХ)

Основні теоретичні відомості

[1]– гл.ІХ, §1, с.478-481; [2] –глава 10, §3, с.595-599; [3]–глава ХV, §1-4, с.208-224; [4] – глава VII, §8-9, 301-307; [5] – ч.ІІ, глава ІI, §1-2, с.42-50.

Нехай у площині Oxy задано гладку чи кусково-гладку криву AB і на цій кривій визначено обмежену функцію P(x, y). Точка A – початкова, а то-

чка B – кінцева точка кривої.
Розіб’ємо криву	AB точками A = A0, A1, A2,..., Ai−1, Ai,..., An = B на n
довільних частин Ai−1, Ai ,		на кожній з яких виберемо точку Mi(xi; yi ),
i = 1,2,...,n, позначимо
	xi	– проекцію вектора Ai−1Ai на вісь Ox і утворимо
суму
		∑n	P(xi; yi ) xi ,
		i=1

яку називають інтегральною сумою.

Позначимо λ = max	li найбільшу з довжин дуг Ai−1Ai .
i=1,2,...,n

Означення. Якщо при λ → 0 ця інтегральна сума має скінченну границю, яка не залежить ні від способу розбиття кривої AB на частини, ні від вибору в них точок Mi, то цю границю називають криволінійним інтегралом функції P (x, y) по координаті x вздовж кривої AB і позначають

	∫P (x, y)dx.
	AB
Отже,
∫	P (x, y)dx = lim ∑n	P (xi; yi ) xi .
AB	λ→0i=1

Аналогічно вводиться криволінійний інтеграл від функції Q( x, y) по коор-

динаті y:
∫	Q(x, y)dy = lim			∑n	Q(xi; yi ) yi ,
AB			λ →0i=1
де yi − проекція вектора		Ai−1Ai	на вісь Oy .
Суму ∫P (x, y)dx + ∫Q( x, y)dy				називають криволінійним інтегралом
AB	AB

по координатах або криволінійним інтегралом другого роду від функцій P і

Qпо кривій AB і позначають

∫P(x, y)dx + Q(x, y)dy .

Обчислення криволінійного інтеграла другого роду

Нехай крива AB задана параметрично рівняннями x = x(t), y = y(t), α ≤ t ≤ β, де функції x(t) та y(t) на відрізку [α ;β ] неперервні разом із своїми похідними x′(t) та y′(t) , причому точці A кривої відповідає параметр

α , а точці B − параметр β. Тоді

∫P(x, y)dx + Q(x, y)dy = β∫(P(x (t), y(t))x′(t)+ Q(x (t), y(t))y′(t))dt .

AB	α
Якщо крива AB задана рівнянням y = y(x) , a ≤ x ≤ b, де функція y(x)
та її похідна y′(x)	неперервні на проміжку [a;b], то

∫P(x, y)dx + Q(x, y)dy = b∫(P(x, y (x))+ Q(x, y(x)) y′(x))dx.

AB	a
Якщо крива AB задана рівнянням x = x(y), c ≤ y ≤ d , де функція x(y)
та її похідна x′(y)	неперервні на проміжку [c;d], то
∫P(x, y)dx + Q(x, y)dy = d∫(P(x(y), y)x′(y)+ Q(x( y), y ))dy .
AB	c

Нехай функції P(x, y, z), Q(x, y, z), R(x, y, z) визначені і неперервні на кривій AB, яку задано рівняннями x = x(t), y = y(t), z = z(t), α ≤ t ≤ β, де функції x(t) , y(t) , z(t) та їхні похідні x′(t) , y′(t) , z′(t) неперервні на проміжку [α ;β ]. Тоді

∫Pdx + Qdy+ Rdz =

=β∫(P(x(t), y(t), z(t))x′(t)+ Q(x(t), y(t),z(t))y′(t)+ R(x(t), y(t), z(t))z′(t))dt.

Криволінійний інтеграл ІІ роду має властивості аналогічні властивостям визначеного інтеграла.

На відміну від криволінійного інтеграла першого роду криволінійний інтеграл другого роду залежить від напряму шляху інтегрування і при зміні цього напряму змінює свій знак:

∫P dx + Q dy = − ∫P dx + Q dy .

AB BA

На незамкненій кривій AB додатнім вважають напрямок, якому відповідає зростання параметра t . Якщо крива AB замкнена ( A = B ), то додатнім вважається той напрямок обходу кривої (контуру), при якому обмежена нею область залишається від спостерігача увесь час зліва (рух проти годинникової стрілки). Протилежний напрямок руху по кривій називають від’ємним.

Криволінійний інтеграл по додатньо орієнтованому контуру L позначають так:

∫P (x, y)dx + Q(x, y)dy.

Питання для самоконтролю

1.Дайте означення криволінійного інтеграла ІІ роду по кривій AB функції Q(x, y) по змінній y .

2.Як обчислюється криволінійний інтеграл ІІ роду, якщо крива AB задана параметрично?

3.Як обчислюється криволінійний інтеграл ІІ роду, якщо крива AB задана явно?

4.Як визначають додатній напрям на замкненій та незамкненій кривій?

Зразки розв’язування задач

Приклад 1. Обчисліть криволінійний інтеграл

∫(x2 − y2 )dx + xydy,

де L − відрізок прямої від A(1;1) до B(3;4).

Розв’язання.

Рівняння прямої, що проходить через дві точки, має вигляд:

AB :		x −1			=						y −1						3(x −1)= 2(y −1) 3x − 3 = 2y − 2 y =																																									3x −1			.
AB :					=												3(x −1)= 2(y −1) 3x − 3 = 2y − 2 y =																																												.
		3 −1									4 −1																																														2
Тоді dy =							3			dx,							1≤ x ≤ 3. Звідки маємо:
Тоді dy =										dx,							1≤ x ≤ 3. Звідки маємо:
						2
																						3						3x −1									2					3				3x −1					3
∫(x2 − y2 )dx + xydy = ∫ x																								2		−		3x −1											dx + ∫x							3x −1					3				=
																								2																													dx
																																																					dx
L																															2											1					2				2
L																						1																				1
				3									2		− 9x					2	+ 6x			−1								2		− 3x											3		(4x2 + 3x −1)dx =
			= ∫					4x							− 9x						+ 6x			−1			+			9x				− 3x						dx =			1		∫
			= ∫																								+													dx =					∫
																			4														4										41
				1															4														4										41
				1					4					3				3			2					3				1			4				3				3		2							4				3
		=										x				+				x		− x						=							3					+		3			− 3 −							+				−1 =
		=										x				+				x		− x						=							3					+		3			− 3 −							+				−1 =
				4					3									2							1					4	3										2									3 2
				1												27							4			3										1											4		1			134					134			67
		=				36 +													−		3 −			−					+1				=					34			+12 −							=								=			=			.
		=				36 +													−		3 −			−					+1				=					34			+12 −							=								=			=			.
				4												2							3			2										4											3		4 3								12			6
		Приклад 2. Обчисліть криволінійний інтеграл
																															∫		x2dy − y2dx
																																												,
																																					5				5			,
																															L
																															L					x3 + y3
																																				x3 + y3
де L − дуга кривої																					x = Rcos3 t,										y = Rsin3 t,												що проходить від точки A(R;0)
до точки B(0;R).
		Розв’язання.
		Відповідно до рівнянь дуги																																		dx = −3Rcos2 tsint dt,																				dy = 3Rsin2 tcost dt .
При русі від точки A до точки B величина x																																															змінюється від R до 0, а y −
від 0 до R , тому параметр t																													змінюється від 0 до π . Отже,
																π																															2
																π
	x2dy − y2dx															2			R2 cos4 t 3Rsin2 t cost + R2 sin6 t 3Rcos																																				2 tsint				dt =
∫															= ∫
∫		5				5									= ∫																		5									5
l		5				5										0																	5									5

	x	3 + y3																													R3 cos5 t + R3 sin5 t
	x	3 + y3																													R3 cos5 t + R3 sin5 t

π	3R3 sin2 tcos2 t(cos5 t + sin		5 t)
2
= ∫				dt =
	5	(cos5 t + sin5 t)
0

	R3

4	2
		2 tsin	2 t dt =
3R3	∫ cos
	0

		4	π			4	π				4				π		4
			π				π
	3		2		3		2	1− cos4t		3			1			3π
	3		2	2 2t dt =	3		2	1− cos4t		3			1			3π
=		R3	∫ sin			R3	∫		dt =		R3	t −		sin 4t	2 =		R3.
=		R3	∫ sin			R3	∫		dt =		R3	t −		sin 4t	2 =		R3.
	4		0		4		0	2		8			4			16
			0				0								0
															0

Задачі для самостійного розв’язування

Обчисліть криволінійні інтеграли:

9.1. ∫x dy, де L − контур трикутника утвореного осями координат і

прямою x + y = 1, обійдений в додатному напрямку.

9.2. ∫(x2 − y2 )dx, де L − дуга параболи y = x2 від точки (0;0) до точки

(2;4).

9.3.	∫(x2 + y2 )dx, де L − контур чотирикутника з вершинами в точках
	L
	A (0;0), B (2;0), C (4;4), D(0;4) (точки вказані в порядку обходу).
9.4.	∫ ydx − xdy, де L − еліпс						x = acost, y = bsint (напрямок обходу –
	L
	додатній).
9.5.	∫(2a − y)dx − (a − x)dy, де						L − перша (від початку координат) арка
	L
	циклоїди x = a(t − sint),					y = a(1− cost).
9.6.	∫xdx + ydy + (x + y −1)dz,						де L − відрізок прямої від точки (1;1;1)
	L
	до точки (2;3;4).
9.7.	∫ yz dx + zx dy + xy dz,					де	L −	дуга гвинтової лінії x = Rcost ,
	L
	y = Rsint,	z =		at	від точки перетину лінії з площиною z = 0 до то-
	y = Rsint,	z =			від точки перетину лінії з площиною z = 0 до то-
				2π
	чки її перетину з площиною z = a.
9.8.	∫(x + y2 )dx + ydy, де L − відрізок прямої y = x −1 від точки A (1;0)
	L
	до точки B(−1;− 2 ).
9.9.	∫4xsin2 ydx + ycos2 2xdy,						де	L − відрізок прямої між точками
	L
	O(0;0) і A (3;6).

9.10.	∫ yz dx + z		R2 − y2 dy + xy dz, де L − дуга гвинтової лінії x = Rcost ,
	L
	y = Rsint,	z =		at	від точки перетину лінії з площиною z = 0 до то-
	y = Rsint,	z =			від точки перетину лінії з площиною z = 0 до то-
				2π

чки її перетину з площиною z = a.

Відповіді: 9.1. 3. 9.2. − 56. 9.3. 112. 9.4. − 2π ab. 9.5. π a2 . 9.6. 13.

153

9.7.0. 9.8. − 2. 9.9. 18. 9.10. 0.

Розрахункові завдання

Задача 13. Обчисліть криволінійні інтеграли ІІ роду.

∫

−

якщо L − чверть кола x = rcost,

y =rsint,

що пробігається

проти руху годинникової стрілки, π ≤ t ≤ π.

∫xy dx + yz dy + zx dz, де L − чверть кола

x = cost,

y =sint, z =1, що

пробігається в напрямку зростання параметра t, 0 ≤ t ≤ π .

∫

dx −

, де L − відрізок циклоїди x = a(t − sint), y = a(1− cost)

− a

від точки t = π до точки t = π .

4.	∫x2 dx − y dy, де L − дуга		астроїди x = acos3 t, y = asin3 t			від точки
	L
	A(a;0) до точки B(0;a ).
5.	∫(x2 − y2 )dx + (x2 + y2 )dy,		в додатному	напрямі	по	еліпсу
	L
	L: x = acost, y = bsint.
6.	∫(2a − y)dx + xdy, де L − арка циклоїди x = a(t − sint),				y = a(1− cost)
	L
	(0 ≤ t ≤ 2π ).
7.	∫(x + y)dx + (x − y)dy, де L − еліпс x = acost,			y = bsint що пробігається
	L
	проти руху годинникової стрілки.
8.	∫(x + y)dx − (x − y)dy , де L − коло x = acost,			y = asint що пробігається
	L	x2 + y2
	L
	проти руху годинникової стрілки.
9.	∫ y2 dx + x2 dy, де L − верхня половина еліпса x = acost, y = bsint що
	L

пробігається за рухом годинникової стрілки.

<<< < Предыдущая 1 2 3 4 56 / 126 7 8 9 10 11 12 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
13.11.2019103.94 Кб2Практика МЭО.doc
#
04.05.20192.6 Mб2ПРАКТИКА ОД.doc
#
08.06.2015128.51 Кб6практика.doc
#
08.06.2015239.1 Кб9практика.doc
#
08.06.2015109.06 Кб19Практика_адвокат_заочка.doc
#
08.06.20151.69 Mб22Практикум з вищої математики.pdf
#
08.06.201519.22 Кб25Практическая 4.docx
#
03.08.2019214.53 Кб2Практична робота5.doc
#
07.05.2019326.14 Кб2Практичне занятт1.doc
#
08.06.201533.86 Кб85ПРИВАТНИЙ ВИЩИЙ НАВЧАЛЬНИЙ ЗАКЛАД.docx
#
11.11.2019264.7 Кб3программа по налоговой системе.doc