
Практикум з вищої математики
.pdf6.2.Знайдіть координати центра мас однорідного тіла, обмеженого поверхнями:
а) |
2x + 3y −12 = 0, x = 0, y = 0, |
z = 0,z = |
y2 |
; |
|
||||
|
|
2 |
|
|
б) |
x = 5, y = 5, z = 0,z2 = xy ; |
|
|
|
в) (x2 + y2 + r2 )2 = a3z.
6.3.Неоднорідне тіло обмежене площинами x = 2, y = 0, y =1,z = 0 і ци-
ліндром z2 = 6x. Об’ємна густина речовини в кожній її точці пропорційна її віддалі від площини Oxy . Знайдіть момент інерції цього тіла відносно осі Oz.
6.4.Знайдіть масу куба, ребро якого дорівнює 1, якщо густина його в точці (x, y,z) дорівнює γ (x, y,z) = x + y + z .
6.5.Знайдіть моменти інерції відносно координатних площин однорідних тіл, обмежених такими поверхнями:
а) |
x2 = y2 + z2, x = h,(h > 0, x ≥ 0); |
|
|||||||||||||||||||||||||||||||||||||||||
б) |
x |
+ |
y |
+ |
|
z |
= 1, x = 0, y = 0, z = 0; |
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
a |
|
|
b |
|
|
|
|
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
в) |
x2 |
+ |
|
y2 |
|
+ |
z2 |
|
= 1, |
x2 |
+ |
|
y2 |
|
= |
x |
. |
|
|
||||||||||||||||||||||||
|
b2 |
|
c2 |
a2 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
a2 |
|
|
|
|
|
|
|
|
|
|
|
|
b2 |
|
|
|
|
a |
|
|
|||||||||||||||||||||
|
|
|
|
Відповіді: 6.1. |
|
а) π |
; |
|
|
б) 4π ; в) |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
6 |
|
|
12 |
|
|
8 |
|
|
|
16 |
|
16 |
|
11 |
|
|
|
|
|
|
||||||||||||||||||
6.2. а) ( |
|
; |
|
|
|
; |
|
|
);б) ( |
|
|
|
; |
|
|
; |
|
|
|
|
);в) (0;0; |
||||||||||||||||||||||
5 |
|
|
5 |
5 |
5 |
|
5 |
|
|
|
3 |
||||||||||||||||||||||||||||||||
б) |
|
I |
|
|
= |
abc3 |
|
, I |
|
= |
a3bc |
, I |
|
|
|
= |
ab3c |
; |
|||||||||||||||||||||||||
|
xy |
|
|
yz |
|
zx |
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
60 |
|
|
|
|
|
|
|
60 |
|
|
|
|
|
|
|
|
|
60 |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
16 |
π ; |
г) |
π |
|
; |
д) 8; |
е) |
π ; |
є) |
|
7 |
. |
|
|||||||
|
3 |
2 |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
12 |
|
|
|||||||
9a |
) |
. 6.5. а) I |
|
= I |
|
= |
πh5 |
, I |
|
= |
πh5 |
; |
||||||||
|
|
xy |
xz |
|
yz |
|
||||||||||||||
20 |
20 |
5 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
в) I |
|
= |
|
|
2 |
abc3(15π −16), |
|
|
|
|
||||||||
|
|
xy |
225 |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
2ab3c |
|
2 |
3 |
|
Ixz = |
|
(105π −272),Iyz = |
|
|
a bc(105π −92). |
1575 |
|
|
|||
|
|
1575 |
|||
Розрахункові завдання
Задача 9. Знайдіть об’єм тіла обмеженого поверхнями.
1.z =1− 6(x2 + y2), z =12x +1.
2.z = 5 − 3((x −1)2 + y2), z = 6x −1.
3.z = −10(x2 + y2) − 9, z =1= 20x − 9 .
4.z =17((x −1)2 + y2) + 7, z = 41− 34x .
5.z = 2 − 4(x2 + y2), z = 8z + 2 .
40

6. z = 7 − 5((x +1)2 + y2), z =10x − 3.
7.z = 8(x2 + y2) − 3, z = −16x − 3.
8.z =19((x −1)2 + y2) − 5, z = 33 − 38x.
9.z = 3 + 2(x2 + y2), z = −4y + 3.
10.z =12((x +1)2 + y2) +1, z = 24x + 25.
11.z =10(x2 + y2) + 8, z = 20y + 8.
12.z =13((x +1)2 + y2) − 48, z = 26x + 22.
13.z = 5 − 3(x2 + y2), z = −6y + 5 .
14.z = −15((x −1)2 + y2) − 5, z = 30x − 35.
15.z = −8(x2 + y2) − 3, z = −16x − 3.
16.z =13 − 7((x −1)2 + y2), z =14x −1.
17.z = 5(x2 + y2) − 2, z =10x − 2.
18.z = 25(x2 + (y +1)2) +1, z = 50y + 51.
19.z = 3 − 4(x2 + y2), z = 8y + 3.
20.z = 20(x2 + (y −1)2) − 2, z = 38 − 40y .
21.z = 7(x2 + y2) −1, z = −14y −1.
22.z =15 − 8((x −1)2 + y2), z =16x −1.
23.z = 4 − 3(x2 + y2), z = 4 + 6x .
24.z =1−16(x2 + (y −1)2), z = 32y − 31.
25.z = 3 −12(x2 + y2), z = 3 + 24x .
Задача 10. Знайдіть координати центра мас однорідного тіла, яке обмежене поверхнями.
1. x + y =1,z = x2 + y2, x = 0, y = 0, z = 0 .
2.z2 = xy, x = 5, y = 5, z = 0.
3.x = 0, y = 0, z = 0,2x + 3y −12 = 0, z = 12 y2.
4.y = 3 − x2 − z2, y ≥ 0.
5.x + y = a,x = z2 + y2, x = 0, y = 0, z = 0 .
6.4x = 2z2 + y2, x = 2.
7.z =1− 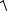
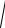 x2 + y2 , z ≥ 0.
x2 + y2 , z ≥ 0.
41

8.z = 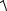
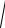 R2 − x2 − y2 , z = 0.
R2 − x2 − y2 , z = 0.
9. |
x + y + z = 3, x = 0, y = 0, z = 0,x =1, y =1. |
|||||||
10. |
z =1− x2 − y2, z ≥ 0. |
|||||||
11. |
x2 + y2 + z2 = 3a2,2az = x2 + y2 (a > 0) . |
|||||||
12. |
x + 2y − z =1, |
|
x = 0, y = 0, z = 0 . |
|||||
13. |
x2 |
+ |
y2 |
= |
|
z2 |
|
, z = 4. |
9 |
|
|
|
|||||
|
4 |
16 |
|
|
||||
14. |
x2 |
+ |
y2 |
+ |
z2 |
|
=1,x = 0, y = 0, z = 0 . |
|
16 |
|
|
|
|||||
|
9 |
4 |
|
|
||||
15.x2 + z2 = 25,z2 + y2 = 25 (z ≥ 0) .
16.x2 + y2 = 2z, x + y = z .
17.x2 + y2 + z2 = 4,x2 + y2 = 3z .
18.x2 + y2 = z,z = 4 .
19.z = x2 + y2, z = 2x + 2y .
20.z = x2 + y2, x2 + y2 =16, x = 0, y = 0, z = 0.
21. |
x2 |
+ |
|
y2 |
+ |
z2 |
|
=1, z = 0. |
|||
4 |
|
|
|
|
|
||||||
|
9 |
|
16 |
|
|
||||||
22. |
z = 4x2, |
z = 0, y = 0, x + y = 6. |
|||||||||
23. |
z = 4 − x2 − y2,z = 3, x = 0, y = 0. |
||||||||||
24. |
z = 2x2 + y2, x + y = 3,x = 0, y = 0,z = 0 . |
||||||||||
25. |
y2 |
|
+ |
z2 |
|
= 2 |
x |
, x = a . |
|||
b2 |
|
c2 |
|
||||||||
|
|
|
|
|
|
a |
|||||
42
§7. КРИВОЛІНІЙНІ ІНТЕГРАЛИ І РОДУ (ПО ДОВЖИНІ ДУГИ)
Основні теоретичні відомості
[1]– гл.ІХ, §1, с.478-481; [2] –глава 10, §3, с.595-599; [3]–глава ХV, §1-4, с.208-224; [4] – глава VII, §8-9, 301-307; [5] – ч.ІІ, глава ІI, §1-2, с.42-50.
Неперервна крива x = x(t), |
y = y(t) називається гладкою на відрізку |
α ≤ t ≤ β, якщо функції x(t), y(t) |
мають на цьому відрізку неперервні похід- |
ні x′(t), y′(t) , які одночасно не дорівнюють нулю. Якщо неперервна крива складається із скінченого числа гладких кривих, її називають кусковогладкою.
Нехай у площині Oxy задано гладку чи кусково-гладку криву |
AB, на |
|||
якій визначено обмежену функцію |
f (x, y). |
|
|
|
Розіб’ємо криву AB точками |
A = A0, Ai ,..., An−1, An = B на n довільних |
|||
частин. Довжини цих частин |
Ai−1Ai , i =1,2,...,n, позначимо li . На кожній |
|||
дузі Ai−1Ai виберемо довільну точку Mi (xi; yi ) і утворимо суму |
|
|||
|
n |
|
|
|
|
∑ f (xi, yi ) |
li , |
(1) |
|
|
i=1 |
|
|
|
яку називають інтегральною сумою функції |
f (x, y) по кривій AB. |
|
||
Позначимо λ = max |
li найбільшу з довжин дуг Ai−1Ai . |
|
||
i=1,2,...,n |
|
|
|
|
Означення. Якщо при λ → 0 інтегральна сума (1) має скінченну границю, яка не залежить ні від способу розбиття кривої AB на частини ні від вибору в них точок Mi , то цю границю називають криволінійним інтегралом першого роду (або криволінійним інтегралом по довжині дуги) від функції f (x, y) по кривій AB і позначають
∫ f (x, y) dl .
AB
У такому разі функція f (x, y) називається інтегровною на кривій AB, а сама
крива AB – кривою інтегрування, |
A – початковою, B – кінцевою точками |
|
інтегрування. |
|
|
Теорема (достатня умова |
інтегровності |
функції). Якщо функція |
z = f (x, y) неперервна на кусково-гладкій кривій |
L, то вона інтегровна по |
|
цій кривій.
Обчислення криволінійних інтегралів першого роду
Нехай крива L задана параметрично рівняннями:
x = x(t),
=
y y(t),
причому функції x(t), y(t) неперервні разом із своїми похідними x'(t), y'(t) на відрізку [α,β ], а функція f (x, y) неперервна на кривій L, тоді
43
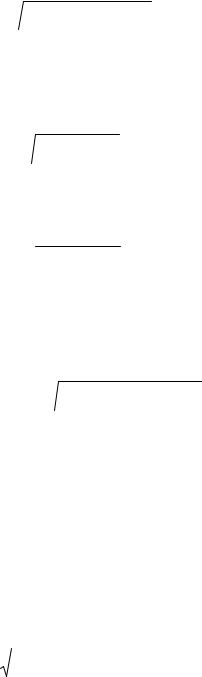
β
∫ f (x, y)dl = ∫ f (x(t), y(t)) 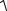 (x′(t))2 + (y′(t))2dt .
(x′(t))2 + (y′(t))2dt .
Lα
Якщо крива L в |
декартових координатах задана рівнянням |
y = y(x), a ≤ x ≤ b, і функція |
y(x) неперервна разом із своєю похідною y'(x) |
на відрізку [a;b], то |
|
b
∫ f (x, y)dl = ∫ f (x, y(x)) 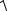 1+ (y′(x))2dx.
1+ (y′(x))2dx.
La
Якщо L задається рівнянням x = x(y), (c ≤ y ≤ d) і функції x(y), x'(y) неперервні на відрізку [c;d], то
∫ f (x, y)dl = d∫ f (x(y), y) 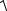
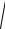 1+ (x′(y))2dy.
1+ (x′(y))2dy.
L |
|
|
c |
|
Якщо крива |
L |
задана |
в полярній системі координат |
рівнянням |
ρ = ρ(ϕ), α ≤ϕ ≤ β , |
і |
функція |
ρ(ϕ) неперервна разом із своєю |
похідною |
ρ′(ϕ) на відрізку [α;β ], то
β
∫ f (x, y)dl = ∫ f (ρ(ϕ)cosϕ, ρ(ϕ)sinϕ) 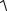 (ρ(ϕ))2 + (ρ′(ϕ))2dϕ .
(ρ(ϕ))2 + (ρ′(ϕ))2dϕ .
Lα
Якщо функція f (x, y,z) визначена і неперервна на просторовій кривій
L, яку задано рівняннями |
|
x = x(t), |
|
|
α ≤ t ≤ β , |
y = y(t), |
|
|
|
z = z(t), |
|
де функції |
x(t), y(t), z(t) та x'(t), y'(t), z'(t) неперервні на відрізку [α,β ], то |
||||
існує криволінійний інтеграл ∫ f (x, y,z)dl |
і справедливою є формула: |
||||
|
L |
|
|
|
|
|
β |
|
|
|
|
∫ f (x, y,z)dl = ∫ f (x(t), y(t),z(t)) |
(x′(t))2 + (y′(t))2 + (z'(t))2dt . |
||||
L |
α |
|
|
|
|
|
Питання для самоконтролю |
|
|||
1. Дайте |
означення криволінійного |
інтеграла |
першого роду |
функції |
|
f (x, y) по кривій L. |
|
|
|
|
|
2. Сформулюйте достатню умову існування |
криволінійного |
інтеграла |
|||
І роду.
3.Сформулюйте правило обчислення криволінійного інтеграла І роду, якщо крива задана параметрично.
4.Сформулюйте правило обчислення криволінійного інтеграла І роду, якщо крива задана явно в декартовій системі координат.
5.Сформулюйте правило обчислення криволінійного інтеграла І роду, якщо крива задана в полярній системі координат.
44

Зразки розв’язування задач
Приклад 1. Обчисліть криволінійний інтеграл
∫(x2 + y2 + z2 )dl,
L
де L − дуга гвинтової лінії x = acost, y = a sint, z = bt (0 ≤ t ≤ 2π ).
Розв’язання.
dl = 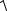
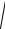 (x′(t))2 + (y′(t))2 + (z′(t))2dt =
(x′(t))2 + (y′(t))2 + (z′(t))2dt = 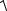
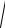 (− asint)2 + (acost)2 + b2dt =
(− asint)2 + (acost)2 + b2dt =
= 
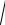 a2 sin2 t + a2 cos2 t + b2dt =
a2 sin2 t + a2 cos2 t + b2dt = 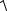
 a2(sin2 t + cos2 t)+ b2dt =
a2(sin2 t + cos2 t)+ b2dt = 
 a2 + b2dt . ∫(x2 + y2 + z2 )dl = 2∫π ((acost)2 + (asint)2 + (bt)2 )
a2 + b2dt . ∫(x2 + y2 + z2 )dl = 2∫π ((acost)2 + (asint)2 + (bt)2 ) 
 a2 + b2dt =
a2 + b2dt =
L |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2∫π (a2 cos2 t + a2 sin2 t + b2t2)dt = |
|
|
|
2∫π (a2 + b2t2)dt = |
|||||||||||
= |
a2 + b2 |
a2 + b2 |
||||||||||||||||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
t |
3 |
|
|
2π |
|
|
|
|
b |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||
= |
a2 + b2 a |
2t + b2 |
|
|
|
= |
a2 + b2 |
|
2πa2 + |
|
8π 3 |
= |
||||||
|
|
|
|
|||||||||||||||
|
|
|
|
3 |
|
|
|
|
|
|
3 |
|
|
|
||||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
=2π 
 a2 + b2 (3a2 + 4π 2b2 ). 3
a2 + b2 (3a2 + 4π 2b2 ). 3
|
|
|
Приклад 2. Обчисліть криволінійний інтеграл |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
∫ |
|
|
dl |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
L |
x2 + y2 + 4 |
|||||
де L − відрізок прямої, що з’єднує точки (0;0) і (1;2). |
||||||||||||||||||
|
|
|
Розв’язання. |
|
|
|
|
|
||||||||||
|
|
|
Рівняння прямої, що проходить через дві точки A(x1; y1) та B(x2; y2 ) |
|||||||||||||||
|
x − x1 |
= |
y − y1 |
. Тоді L має рівняння: |
||||||||||||||
|
|
|
||||||||||||||||
|
x |
2 |
− x |
y |
2 |
− y |
|
|
|
|
|
|||||||
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
x − 0 |
= |
y − 0 |
x = |
y |
y = 2x , (0 ≤ x ≤1). |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
1− 0 2 − 0 |
2 |
|
|
|
|||||
dl = 
 1+ (y′(x))2dx =
1+ (y′(x))2dx = 
 1+ 22dx =
1+ 22dx = 
 5dx.
5dx.
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
||||||||||||
|
|
|
dl |
|
|
|
|
|
|
5dx |
|
|
|
|
|
dx |
dx |
|
|
|||||||||||||||||||||||||||||
∫ |
|
|
|
|
= ∫ |
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
5 |
∫ |
|
|
|
|
|
= |
5 |
∫ |
|
|
= |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
2 + (2x)2 + 4 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
L x |
2 + y2 + 4 0 x |
|
|
|
|
|
|
0 x |
2 + 4x2 + 4 |
|
|
|
0 5x2 + 4 |
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
= ln |
x + x2 + |
4 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
= |
5 |
∫ |
|
|
|
|
|
|
|
= |
∫ |
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
0 |
|
|
|
2 |
+ |
4 |
0 |
|
|
2 |
+ |
4 |
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
5 x |
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
45 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
3) |
|
|
|
|
|
|
||||||||||
= ln1+ 1+ |
4 |
|
|
|
− ln |
0 + |
|
0 + |
4 |
|
= ln1+ |
3 |
|
|
|
− ln |
2 |
|
= ln |
|
( 5 |
5 |
|
= |
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
5 |
|
|
|
5 |
|
|
|
|
|
|
5 2 |
|
|
|
|
|
|
|||||||||||||
= ln |
|
|
|
|
|
|
|
|
|
|
|
= ln |
|
|
|
+ 3 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
5 |
+ 3 |
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задачі для самостійного розв’язування |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
Обчисліть криволінійні інтеграли I роду. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
7.1. |
∫ |
|
|
|
|
|
|
|
|
dl |
|
|
|
|
|
|
, |
|
|
де |
L − відрізок |
прямої |
y = |
x |
− 2, |
що з’єднує |
точки |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
L |
|
|
|
|
|
x2 + y2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
(0;−2) і (4; 0). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
7.2. |
∫xy dl, |
|
|
|
|
|
|
де |
|
|
|
|
L − контур |
прямокутника |
|
з |
вершинами |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A(0;0), B(4;0), C(4;2), D(0,2). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
7.3. |
∫ |
|
|
|
dl |
|
, де L − відрізок прямої |
y = |
1 |
x − 2 , що знаходиться між точ- |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
− y |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
L |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
ками A(0;−2), B(4;0). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
7.4. |
∫ |
|
|
|
|
|
|
|
dl, де L – перша арка циклоїди x = a(t − sint), y = a(1− cost). |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
2y |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7.5. |
∫ |
|
|
|
|
|
z2dl |
|
, |
|
|
|
|
|
де |
|
|
|
L |
|
|
– |
перший |
|
виток |
гвинтової |
лінії |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
L |
|
x |
2 + y2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
x = acost, |
|
|
|
|
y = asint, z = at . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
7.6. |
∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
2 |
+ y |
2 |
|
, де |
|
L − перший виток конічної гвинтової лінії |
||||||||||||||||||||||||||||||||||||||||||||
2z − |
|
|
|
|
|
|
|
|
|
|
|
|
dl |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
x = tcost, y = tsint, |
|
z = t. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
7.7. |
∫ |
|
|
|
|
x2 + y2dl, де L – коло x2 + y2 = ax . |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7.8. |
∫ ydl, |
|
|
|
де |
|
|
|
|
L |
|
|
– |
дуга |
параболи |
|
|
y2 = 2px, відсічена |
параболою |
||||||||||||||||||||||||||||||||||||||||||||||||
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2= 2py. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
7.9. |
∫ |
ydl |
|
, |
де |
|
|
|
L – дуга параболи |
y2 = |
4 |
x3 від точки (3;2 |
|
) до точки |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
3 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
L |
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
32 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
8; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
7.10. |
∫ |
|
|
|
|
|
|
|
|
|
|
dl |
|
|
|
|
|
|
|
|
, |
|
|
де |
|
L |
|
|
– відрізок |
прямої |
x = 2t, |
|
|
y = 2t − 2, |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
L |
|
x |
|
|
+ 2y + 3z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
z = −t + 2, (0 ≤ t ≤1).
46

Відповіді: 7.1. ln 1 (
 21 +1). 7.2. 24 . 7.3.
21 +1). 7.2. 24 . 7.3. 
 5ln2. 7.4. 4π a
5ln2. 7.4. 4π a
 a . 2
a . 2
7.5. 8aπ |
3 |
2 . 7.6. 2 |
2 (1+ 2π 2 )2 |
−1 . 7.7. 2a2. 7.8. |
p |
2 |
(5 |
5 −1). |
7.9. 2152. |
||||||||||
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
3 |
|
3 |
|
|
|
45 |
|
||||||||||
7.10. ln |
5 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
Розрахункові завдання |
|
|
|
|
|
|
|
|
||
Задача 11. Обчисліть криволінійні інтеграли I роду. |
|
|
|
|
|
|
|
||||||||||||
1. ∫z dl, де L– конічна гвинтова лінія x = t cost, y = tsint, |
z = t |
(0 ≤ t ≤ t0 ). |
|||||||||||||||||
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2. |
∫ |
|
|
|
dl |
|
|
, де L − перший виток конічної гвинтової лінії |
|||||||
|
|
|
|
|
|
||||||||||
|
|
+ y2 |
|
|
|||||||||||
|
L |
x |
2 |
+ z2 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y = asint, |
z = bt . |
|
|
|
|
|
|
|
||||||
|
|
|
|
4 |
|
4 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
x = acos |
3 |
|
y = asin |
3 |
|
|
|
3. |
∫ |
|
3 + y |
3 |
t, |
t |
|||||||||
x |
dl, де L − дуга астроїди |
|
|
0 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
||
x= acost,
≤t ≤ π . 2
|
|
|
|
|
|
|
|
|
y = |
at2 |
|
|
z = |
at3 |
|
||||||
4. |
∫ |
2y |
|
dl, де L − дуга кривої x = at, |
, |
(0 ≤ t ≤ π ). |
|||||||||||||||
|
|
|
|
|
|
||||||||||||||||
|
L |
|
a |
|
|
|
|
2 |
|
|
|
3 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
5. |
∫(x2 + y2 − 2)dl, |
де L − дуга циклоїди |
|
x = a(t − sint), |
y = a(1− cost) |
||||||||||||||||
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(0 ≤ t ≤ π ). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
6. |
∫(x2 + y2 )dl, де L − дуга астроїди x = acos3 t, |
y = asin3 t |
(0 ≤ t ≤ 2π ). |
||||||||||||||||||
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7. |
∫x dl, де L − дуга кривої x = et cost, |
y = et sint, |
z = et (− ∞ < t ≤ 0). |
||||||||||||||||||
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8. |
∫(y2 + z2 )dl, де |
L − перший виток гвинтової лінії |
x = acost, y = asint, |
||||||||||||||||||
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z = |
bt |
(0 ≤ t ≤ 2). |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
2π |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
9. |
∫ y2 dl, де L − арка циклоїди x = a(t − sint), |
|
y = a(1− cost) (0 ≤ t ≤ 2π ). |
||||||||||||||||||
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10. |
∫(x2 + y2 )dl, де L − крива x = a(cost + sint), |
y = a(sint − cost) |
|||||||||||||||||||
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(0 ≤ t ≤ 2π ). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
11. |
∫xy dl, де L − крива x = a |
ex + e− x |
, |
y = a |
ex − e− x |
|
(0 ≤ t ≤ t0 ). |
||||||||||||||
|
|
||||||||||||||||||||
|
L |
|
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
47
12. ∫(x2 + y2 + z2 )dl, де L − частина гвинтової лінії x = acost, y = asint,
L
z = bt (0 ≤ t ≤ 2π ).
13. |
∫ |
(x + z) dl, де L − дуга кривої x = t, y = |
3t |
2 |
|
|
, z = t3 (0 ≤ t ≤1). |
||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||
|
|
||||||||||||||||||||||||
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
14. |
∫ |
|
x2 + y2 dl, де L − крива x = a(cost + tsint), |
y = a(sint − tcost) |
|||||||||||||||||||||
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(0 ≤ t ≤ 2π ). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
2z − |
|
|
dl, |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
15. |
∫ |
x2 + y2 |
де L − |
дуга |
кривої |
x = tcost, |
y = tsint, z = t |
||||||||||||||||||
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(0 ≤ t ≤ 2π ). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
16. |
∫(x2 + y2 )ndl, де L − коло x = acost, |
y = asint . |
|
||||||||||||||||||||||
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
17. |
∫ ye− x dl, де L − частина кривої x = ln(1+ t2), |
y = 2arctgt − t + 3 між то- |
|||||||||||||||||||||||
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
чками t = 0, t =1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
18. |
∫xy zdl, |
де L − |
дуга |
кривої |
x = t, y = |
|
|
8t3 3, z = t2 2 |
між точками |
||||||||||||||||
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t = 0, t =1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
19. |
∫ |
|
x2 + y2 dl, де L − крива x = a(cost + tsint), |
y = a(sint − t cost), |
|||||||||||||||||||||
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(0 ≤ t ≤ 2π ). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
20. |
∫(x2 + y2 )dl, де L − дуга астероїди x = acos3t, |
y = asin3t |
(0 ≤ t ≤ 2π ). |
||||||||||||||||||||||
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
21. |
∫(x + y) dl, де L − крива x = a(cost + tsint), |
|
y = a(sint − tcost), |
||||||||||||||||||||||
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(0 ≤ t ≤ 2π ). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
∫xy zdl, де L − дуга кривої x = |
|
|
t2, |
y = t − t2 |
(−1≤ t ≤1). |
|||||||||||||||||||
22. |
|
3 |
|||||||||||||||||||||||
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
23. |
∫x dl, де L–дуга кривої x = (t2 − 2)sint + 2tcost, y = (2 − t2)cost + 2tsint |
||||||||||||||||||||||||
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
від t = 0 до t = π . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
24. |
∫ |
y |
dl, |
де L − |
дуга кривої x = ln(1+ t2 ), y = 2arctgt − t |
на відрізку від |
|||||||||||||||||||
|
|||||||||||||||||||||||||
|
L e |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
t = 0 до t =1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
25. |
∫ |
(x2 + y2 )dl, де |
L – дуга кривої x =t2, |
y = |
t |
(t2 − 3) між точками пере- |
|||||||||||||||||||
|
|||||||||||||||||||||||||
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
тину з віссю Ox.
48
§8. ЗАСТОСУВАННЯ КРИВОЛІНІЙНИХ ІНТЕГРАЛІВ І РОДУ
Основні теоретичні відомості
[1]– гл.ІХ, §1, с.478-481; [2] –глава 10, §3, с.595-599; [3]–глава ХV, §1-4, с.208-224; [4] – глава VII, §8-9, 301-307; [5] – ч.ІІ, глава ІI, §1-2, с.42-50.
Нехай у площині Oxy задано кусково-гладку криву AB і на цій кривій визначено неперервну функцію f (x, y), тоді:
1)Площу P циліндричної поверхні з напрямною AB, висота якої визначена функцією z = f (x, y), знаходять за формулою
P = ∫ f (x, y) dl.
AB
2) Довжину l кривої AB визначають за формулою
l = ∫ dl.
AB
Нехай вздовж неоднорідної матеріальної дуги L розподілено масу з лінійною густиною ρ (x, y), тоді:
3) Маса дуги L обчислюється за формулою m = ∫ρ (x, y) dl.
L
4) Координати xc , yc центра маси дуги L знаходять за формулою
|
|
|
∫xρ (x, y)dl |
|
M y |
|
∫ y ρ (x, y) dl |
|
M |
|
|
x |
|
= |
L |
= |
; y = |
l |
= |
x |
, |
||
|
|
|
|||||||||
c |
∫ρ (x, y)dl |
|
∫ρ (x, y)dl |
|
|
||||||
|
|
|
m |
c |
|
m |
|||||
|
|
|
L |
|
|
|
L |
|
|
|
|
де M x, M y − статичні моменти кривої L відносно осей Ox і Oy
5)Моменти інерції дуги L відносно осей Ox , Oy та початку координат відповідно дорівнюють
Jx = ∫ y2ρ (x, y)dl; J y = ∫x2ρ (x, y)dl;
L L
J0 = ∫(x2 + y2 )ρ (x, y) dl.
L
Питання для самоконтролю
1.Які геометричні застосування криволінійного інтегралу І роду?
2.Як знайти масу неоднорідної матеріальної дуги?
3.Наведіть формули обчислення статичних моментів та моментів інерції матеріальної дуги.
4.Як знайти положення центру мас неоднорідної матеріальної дуги?
49
