Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Межрегианальная Академия Управления Персоналом

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Практикум з вищої математики

.pdf

Скачиваний:

Добавлен:

08.06.2015

Размер:

1.69 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 78 / 128 9 10 11 12 > Следующая >>>

§12. ПОВЕРХНЕВІ ІНТЕГРАЛИ ПЕРШОГО РОДУ

Основні теоретичні відомості

[1] – гл.ІХ, §2, с.481-486; [2] – глава 10, §4, с.618-621; [3] – глава ХV, §5-6, с.224-229, [4] – глава VII, §11-12, с.311-338, [5] – ч.ІІ, глава ІI, §5, с.52-56.

Поверхня називається гладкою, якщо в кожній точці поверхні існує дотична площина, положення якої неперервно змінюється разом з точкою дотику. Поверхню називають кусково-гладкою, якщо вона складається із скінченого числа неперервно сполучених гладких поверхонь.

Нехай дано гладку або кусково-гладку поверхню S , в точках якої визначена обмежена функція f (x, y, z) . Розіб’ємо за допомогою кусковогладких кривих поверхню S на n частин S1, S2,…, Sn, які не мають спільних внутрішніх точок. Позначимо Si – площу частини розбиття Si , i =1,2,…, n . В кожній із цих частин виберемо довільну точку Mi(xi, yi, zi), Mi Si, і утворимо суму

∑ f (xi, yi, zi ) Si , k=1

яку називають інтегральною сумою.

Позначимо λ = max diam(Si) – найбільший із діаметрів частин Si . i=1,2,..,n

Означення. Якщо інтегральна сума при λ → 0 має скінченну границю, яка не залежить ні від способу розбиття поверхні S на частини Si , ні від вибору в них точок Mi , то ця границя називається поверхневим інтегралом

Іроду від функції f (x, y, z) по поверхні S і позначається

∫∫f (x, y, z)dS .

Обчислення поверхневих інтегралів першого роду

Нехай поверхня S задана рівнянням z = z(x, y) і взаємнооднозначно проектується на площину Oxy в область Dxy . І нехай функція f (x, y, z)

неперервна в усіх точках цієї поверхні. Оскільки, поверхня S гладка, то функція z = z(x, y) неперервна і має неперервні частинні похідні z′x, z′y в

області Dxy . В такому випадку поверхневий інтеграл першого роду

обчислюється за формулою:
∫∫ f (x, y, z)dS = ∫∫ f (x, y, z(x, y)) 1+ z′x	2(x, y) + z′y	2(x, y)dxdy.	(1)

SDxy

Якщо гладку поверхню S задано рівняннями x = x(y,z) або y = y(x,z), то відповідні формули переходу від поверхневого інтеграла І роду до подвійного запишуться так:

∫∫ f (x, y, z)dS = ∫∫ f (x(y, z), y, z) 1+ x′y

2(y, z) + x′z

2(y, z)dydz ,

SDyz

∫∫ f (x, y, z)dS = ∫∫ f (x, y(x, z), z) 1+ y′x

2(x, z) + y′z

2(x, z)dxdz,

SDxz

де Dyz , Dxz – проекції заданої поверхні S на площини Oyz, Oxz.

Питання для самоконтролю

1.Дайте означення поверхневого інтеграла І роду від функції f (x, y,z) по поверхні S .

2.Навдіть формули переходу від поверхневого інтеграла І роду до подвійного інтеграла.

3.Як можна застосувати поверхневий інтеграл І роду до знаходження площі поверхні, маси матеріальної поверхні, статичних моментів та моментів інерції матеріальної поверхні?

Зразки розв’язування задач

Приклад 1. Обчисліть поверхневий інтеграл ∫∫(x − 2y + 3z)dS ,

де S – частина площини 2x + y + 4z = 8, розміщена в І-му октанті.

Розв’язання.

Запишемо					рівняння				площини					у		вигляді				z = 2 −						1		x −				1		y. Застосуємо
Запишемо					рівняння				площини					у		вигляді				z = 2 −								x −						y. Застосуємо
																									2							4
			z						формулу (1), знайшовши:
			z																		1									1
	2																	z′x = −			1	, z′y = −								1	,
	2																	z′x = −				, z′y = −									,
			S			8													2										4
		O			B		y																		1				1						21
		O			B		y										2	2							1				1						21
A													1+ z′x					+ z′y	=				1+				+						=			.
A													1+ z′x					+ z′y	=				1+		4		+		16				=			.
4																									4				16						4
4										Проекцію								площини										2x + y + 4z = 8 на
x										Проекцію								площини										2x + y + 4z = 8 на
x
									площину Oxy є трикутник AOB, обмежений
прямими 2x + y = 8, x = 0, y = 0.
Отже,

												1					1		21
∫∫(x − 2y + 3z)dS = ∫∫							x	− 2y + 3 2			−				x	−		y					dxdy				=
∫∫(x − 2y + 3z)dS = ∫∫							x	− 2y + 3 2			−	2			x	−	4	y	4				dxdy				=
S					D							2					4		4
						xy
								11									4 8−2x							1					11
=	21				6 −	1	x −	11				21					4 8−2x						−	1			−		11
				∫∫						y dxdy	=						∫dx ∫			6					x								y dy =
	4			∫∫		2		4		y dxdy	=	4					∫dx ∫			6				2	x				4				y dy =
	4					2		4				4					0	0						2					4
				Dxy													0	0

		4															8−2x
	21	4				1				11							8−2x
	21					1				11				2
=		∫		6y −			xy	−				y								dx =
=		∫		6y −			xy	−				y								dx =
	4					2				8
		0															0
		0															0
		4
	21	4													2			11					2
=		∫	48		−12x −			4x + x								−			(8		− 2x)			dx =
=		∫	48		−12x −			4x + x								−			(8		− 2x)			dx =
	4	0																8
		0
									x3				11 (8 − 2x)3									4

	21
=			48x		− 8x2 +						+											=
=			48x		− 8x2 +						+											=
	4							3				16						3
	4							3				16						3				0

=	21				−128 +			64			−	352						= −8
	21							64				352
		192																			21.
		192																			21.
	4							3							3

Приклад 1. Обчисліть поверхневий інтеграл

∫∫(x2 + y2 + z)dS ,

де S – частина параболоїда 2z = x2 + y2 , обмежена площиною z = 2.

Розв’язання.

Застосуємо формулу (1). Знаходимо

z′

= x, z′ = y ,

1+ z′ 2

+ z′ 2

= 1+ x2 + y2 .

Тоді

+ y2

∫∫(x2 + y2 + z)dS =

∫∫ (x2 + y2 +

)

1+ x2 + y2dxdy =

Dxy

∫∫(x

+ y

) 1

+ x

+ y

dxdy.

Dxy

Оскільки, область

D – круг x2 + y2 ≤ 4, то

для

обчислення

даного

подвійного інтегралу

Sперейдемо до полярних координат x = ρ cosϕ, y = ρ sinϕ .

						Рівняння кола (межі області D ) набуде вигляду
			O								ρ = 2, 0 ≤ϕ ≤ 2π .
2			O	2		Отже,
2				2		Отже,
x					y		3
x					y			∫∫(x	2 + y	2) 1	+ x2 + y2dxdy =

						2
						2		Dxy
								Dxy
	3	2π	2						2
		2π	2						2
=		∫dϕ ∫ρ 2 1+ ρ 2 ρdρ = 3π ∫ρ2 1+ ρ2ρdρ =
=		∫dϕ ∫ρ 2 1+ ρ 2 ρdρ = 3π ∫ρ2 1+ ρ2ρdρ =
2		0	0						0
		0	0						0

	1		+ ρ 2		= t

	ρ	2	= t	2	−1			t	5
=							= 3π	t
=							= 3π
ρdρ = tdt								5
ρdρ = tdt								5


t1 =1, t2					=	5

	t3	5

				10 5		2
−			= 3π		+		= π 10
−			= 3π		+		= π 10
	3			5		15
		1
		1

Задачі для самостійного розв’язування

Обчисліть поверхневі інтеграли першого роду.

12.1. ∫∫(xy − x + 4z)dS , де S – частина площини

5 + 2 . 5

x + y + z = 2,

розташована в першому октанті.

12.2.

∫∫x2 ydS ,

де

–

бічна

поверхня

конуса

z = x2 + y2 ,

що

відтинається площиною z = 2.

12.3.

∫∫zdS , де

–

частина

поверхні

3z = x2 + y2 , розміщена

між

площинами z = 0, z = 3.

12.4.

∫∫(x + 2y + 3z)dS ,

де

–

частина

площини

2x + 4y + 3z =12,

розміщена в першому октанті.

12.5.

∫∫x2dS , де

– частина поверхні

z −1= −x2 − y2 , розміщена над

площиною Oxy.

12.6. ∫∫ y2dS , де S – півсфера z = 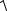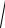9 − x2 − y2 .

12.7. ∫∫zdS , де S – бічна поверхня конуса z = 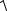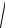x2 + y2 , що відтинається

площиною z =1.

12.8.

∫∫(x2 + y2)dS , де S – півсфера z =

4 − x2 − y2 .

12.9.

∫∫(x + 5y + 2z)dS , де S

– частина площини x + y + z = 3, розміщена

в першому октанті.

12.10. ∫∫xydS , де

S – частина поверхні

z − 9 = −x2 − y2, розміщена над

площиною Oxy.

=1,

12.11. ∫∫ z + 2x

y dS , де

S – частина площини

розміщена в першому октанті.

12.12. ∫∫xyzdS ,	де	S	–	частина	площини x + y + z =1,	розміщена	в
S
першому октанті.
12.13. ∫∫x2dS ,	де	S	–	частина	сфери x2 + y2 + z2 = 4,	розміщена	в
S

першому октанті.

12.14. ∫∫ ydS , де S – півсфера z = 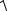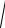R2 − x2 − y2 .

				S																														(x				2 + y2 )
12.15. ∫∫xdS , де																												z = 2 −						(x				2 + y2 )
												S		– частина поверхні																														, розміщена над
												S		– частина поверхні																									2					, розміщена над
				S																																			2
				S
		площиною Oxy.
12.16. ∫∫							dS						, де				S – частина площини																		x + y + z =1, розміщена в

					(1+ x			+ y)				2
				S	(1+ x			+ y)				2
				S
		першому октанті.

12.17. ∫∫zdS ,									де			S			–		бічна поверхня											конуса											z =				x2 + y2 ,		вирізану
				S
		циліндром x2 + y2 = 2x .
12.18. ∫∫ ydS , де S – півсфера z =																							9 − x2 − y2 .
				S
12.19. ∫∫xdS ,									де			S			–		частина				площини										z = y ,									обмежена площинами
				S
				x + y = 2, x = 0, y = 0, z = 0.

12.20. ∫∫(xy + yz + zx)dS , де S																				–		частина							конуса											z = x2 + y2 ,						вирізана
				S
		поверхнею x2 + y2 = 2ax.

											14			3										27						10			5						2
											14			3										27						10			5						2
Відповіді: 12.1.																. 12.2. 0.				12.3.							π									+						. 12.4. 24			29 .
Відповіді: 12.1.																. 12.2. 0.				12.3.							π									+						. 12.4. 24			29 .
												3												8						3									15
												3												8						3									15
	π																																				64π
	π		10			5		2														2		2													64π
12.5.							+					. 12.6. 54π . 12.7.														π .				12.8.												. 12.9. 36. 12.10. 0.
12.5.							+					. 12.6. 54π . 12.7.														π .				12.8.												. 12.9. 36. 12.10. 0.
16					3			15														3																	3
16					3			15														3																	3
																			π									+ 2
												13										782			17
												13										782			17
12.11. 4			61.			12.12.
														. 12.13.
														. 12.13.																		. 12.14. 0. 12.15. 0.
												120							64					15
								1									2	π . 12.18. 0.															4					2				64 2					a4 .
								1									2																4					2				64 2
12.16.		3 ln2 −								.		12.17.															12.19.														. 12.20.
12.16.		3 ln2 −								.		12.17.															12.19.														. 12.20.
								2									3																			3						15

10. ∫∫(x2 + y2)dS , де S – сфера x2 + y2 + z2 =1.

1. ∫∫

Розрахункові завдання

Задача 16. Обчисліть поверхневі інтеграли І роду.

(3x − y + 4z)dS , де S – частина площини, розміщена в першому

октанті.

∫∫(y + z +

4 − x2 )dS ,

де

– поверхня

циліндра

x2 + y2 = 4, що

знаходиться між площинами z = 0 і z = 2.

∫∫dS , де S – півсфера z =

4 − x2 − y2 .

∫∫(x2 + y2)dS , де

– поверхня, що відтинається

від параболоїда

x2 + y2 = 2z площиною z =1.

∫∫(x2 y2 + x2z2 + y2z2)dS , де S – поверхня, що відтинається від конуса

z =

x2 + y2 площиною z = 2.

∫∫xdS , де S – півсфера z =

1− x2 − y2 .

∫∫

, де

– частина площини

x + y + z =1, розміщена в

+ x + y)

першому октанті.

∫∫ ydS , де S – півсфера z =

9 − x2 − y2 .

∫∫x2 y2dS , де S – півсфера z =

1− x2 − y2 .

11.

∫∫

, де

–

частина

поверхні

циліндра x2 + y2 =1,

що

2 + y2 + z2

відтинається площинами z = 0 і z = 2.

12.

∫∫

x2 + y2 dS ,

де

–

бічна

поверхня

конуса

z2 = x2 + y2 ,

що

відтинається площиною z = 2.

13.

∫∫(x2 + y2)dS ,

де

–

бічна

поверхня

конуса

z = x2 + y2 ,

що

відтинається площиною z = 2.

14. ∫∫zdS , де S – частина поверхні циліндра x2 + z2 = 4, що відтинається

площинами y = 0 і y = 3.

15.

∫∫

, де

– поверхня площини x + y + z =1,

розміщена в

(1+ x + y)2

першому октанті.

16.

∫∫

5x + 2z

dS , де

– частина площини

2x + y + 2z − 2 = 0, розміщена в

першому октанті.

17.

∫∫zdS ,

де

–

частина

поверхні

z = 4 − x2 − y2 ,

розміщена

над

площиною Oxy.

18.

∫∫xdS ,

де

–

частина

площини

z = y ,

обмежена

площинами

x + y = 2, x = 0, y = 0.

19.

∫∫(x − 3y + 2z)dS , де S – частина площини x + 2y + 4z = 4, розміщена в

першому октанті.

20.

∫∫(x2 + y2)dS , де

– частина поверхні

z = x2 + y2, що відтинається

площиною z =1.

21.

∫∫ ydS ,

де

–

частина

поверхні

z =1− x2 − y2 ,

розміщена

над

площиною Oxy.

22.

∫∫xyzdS , де

–

частина поверхні

z = x2 + y2,

розміщена

між

площинами z = 0, z = 2.

23.

∫∫xdS ,

z = 2 −

+ y2

де

–

частина

поверхні

розміщена

над

площиною Oxy.

24.

∫∫

x2 + y2 dS , де S – півсфера z = 1− x2 − y2 .

25.

∫∫xydS ,

де

–

частина

поверхні

z = x2 + y2,

що

відтинається

площиною z =1.

§13. ПОВЕРХНЕВІ ІНТЕГРАЛИ ДРУГОГО РОДУ

Основні теоретичні відомості

[1]– гл.ІХ, §2, с.481-486; [2] –глава 10, §4, с.621-626; [3]–глава ХV, §5-6, с.224-229, [4] – глава VII, §11-12, с.311-338, [5] – ч.ІІ, глава ІI, §5, с.52-56.

Розглянемо гладку поверхню

S . Виберемо на ній деяку точку M і

проведемо через неї довільну замкнену

криву, що не перетинає межу поверхні.

Побудуємо

точці M нормаль n

вибраного

напряму

(рис. 1). Будемо

переміщувати

точку

разом

вектором n по контуру так, щоб n

увесь час залишався нормальним до S .

При цьому можливі два випадки:

1) після обходу контуру повертаємося

Рис. 1

точку

початковим

напрямом

нормалі n;

2) після обходу контуру повертаємося

точку

з напрямом

нормалі,

протилежним початковому.

В першому випадку поверхню S

Рис. 2

називають

двосторонньою.

другому – односторонньою.

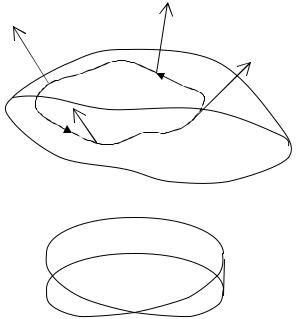
Класичним прикладом односторонньої поверхні є так званий лист Мебіуса (рис. 2). Надалі будемо розглядати лише двосторонні поверхні.

Якщо на двосторонній поверхні вибрано один із двох можливих напрямів нормалі, то таку поверхню будемо називати орієнтованою, а вибір певної сторони поверхні – орієнтацією поверхні.

Нехай дано гладку орієнтовану поверхню S , яка взаємонооднозначно проектується на область D площини Oxy, і нехай в точках поверхні S визначена обмежена функція R(x, y,z). Розіб’ємо за допомогою кусковогладких кривих поверхню S на n частин S1, S2,…, Sn, які не мають спільних внутрішніх точок. Позначимо Di проекцію частини розбиття Si ,

i =1,2,…, n , на площину Oxy, а Si* – площу Di, взяту із знаком «+», якщо нормалі вибраної сторони поверхні утворюють із віссю Oz гострий кут, та із знаком «–», якщо цей кут тупий. В кожній із частин Si виберемо довільну точку Mi(xi, yi, zi ) і утворимо суму

∑R(xi, yi, zi) Si* , k=1

яку називають інтегральною сумою.

Позначимо λ = max diam(Si) – найбільший із діаметрів частин Si . i=1,2,..,n

ІІроду від функції R(x, y,z) по поверхні S і позначається

∫∫R(x, y, z)dxdy .

	S
Отже,
	n
∫∫R(x, y, z)dxdy = lim∑R(xi, yi, zi) Si* .
S	λ→0i=1

З означення поверхневого інтеграла другого роду випливає, що при заміні орієнтації поверхні на протилежну інтеграл змінює свій знак.

Припустимо, що поверхню S можна взаємнооднозначно проектувати також на координатні площини Oxz та Oyz, і нехай P(x, y, z), Q(x, y, z) визначені та обмежені в точках поверхні функції S , тоді аналогічно можна дати означення ще двох поверхневих інтегралів другого роду:

∫∫Q(x, y, z)dxdz і ∫∫P(x, y, z)dydz .

S S

На практиці найпоширенішим є поверхневі інтеграли, які об’єднують усі три названі, тобто

∫∫P(x, y, z)dydz + Q(x, y, z)dxdz + R(x, y, z)dxdy =

= ∫∫P(x, y, z)dydz + ∫∫Q(x, y, z)dxdz + ∫∫R(x, y, z)dxdy.

S S S

Обчислення поверхневих інтегралів другого роду

Нехай функція R(x, y, z) неперервна в усіх точках гладкої поверхні S , яка задана рівняннями z = z(x, y). Поверхня S взаємнооднозначно проектується в область Dxy площини Oxy. Виберемо верхню сторону поверхні S , яку позначимо S+ (сторона поверхні, в кожній точці якої

нормаль утворює з додатним напрямом осі Oz гострий кут), тоді

∫∫R(x, y, z)dxdy = ∫∫R(x, y, z(x, y))dxdy.

S+ Dxy

Якщо вибрати нижню сторону поверхні S− (нормаль до вибраної сторони поверхні утворює з віссю Oz тупий кут), то одержаний подвійний інтеграл беруть зі знаком «мінус», тобто

∫∫R(x, y, z)dxdy = − ∫∫R(x, y, z(x, y))dxdy.

S− Dxy

Аналогічно, якщо гладку поверхню S задано рівнянням x = x(y,z), то

∫∫P(x, y, z)dydz = ∫∫P(x(y, z), y, z)dydz ,

S+ Dyz

∫∫P(x, y, z)dydz = − ∫∫P(x(y, z), y, z)dydz .

S− Dyz

Знак «+» беремо, коли нормаль до поверхні S , утворює з віссю Ox гострий кут, а знак «–», коли кут тупий. Dyz – проекція поверхні S на площину Oyz.

Якщо гладку поверхню S задано рівнянням y = y(x,z), то

∫∫Q(x, y, z)dxdz = ∫∫Q(x, y(x, z), z)dxdz ,

S+ Dxz

∫∫Q(x, y, z)dxdz = − ∫∫Q(x, y(x, z), z)dxdz .

S− Dxz

Знак «+» беремо, коли нормаль до поверхні S , утворює з віссю Oy гострий кут, а знак «–», коли кут тупий. Dxz – проекція поверхні S на площину xOz .

Якщо поверхня неоднозначно проектується на яку-небудь координатну площину, то цю поверхню розбивають на частини, які проектуються взаємнооднозначно, а інтеграл обчислюють як суму інтегралів по одержаних частинах поверхні S .

Зауваження. У випадку, коли потрібно обчислити загальний інтеграл другого роду

∫∫P(x, y, z)dydz + Q(x, y, z)dxdz + R(x, y, z)dxdy ,

по поверхні S , яка задана рівнянням z = z(x, y), можна скористатися

формулою:

∫∫P(x, y, z)dydz + Q(x, y, z)dxdz + R(x, y, z)dxdy =

S±

= ± ∫∫(P(x, y, z(x, y))(−z′x) + Q(x, y, z(x, y))(−z′y ) + R(x, y, z(x, y)))dxdy.

Dxy

Якщо сторона поверхні верхня, тобто нормаль до цієї поверхні утворює з віссю Oz гострий кут, то вибираємо знак «+», якщо нижня то «–».

Якщо P(x, y, z), Q(x, y, z), R(x, y, z) – неперервні функції і S вибрана сторона гладкої поверхні, що характеризується напрямом нормалі n0 (cosα, cosβ, cosγ ), то відповідний поверхневий інтеграл другого роду

виражається через поверхневий інтеграл першого роду за формулою:

∫∫P(x, y, z)dydz + Q(x, y, z)dxdz + R(x, y, z)dxdy =

= ∫∫(P(x, y, z)cosα + Q(x, y, z)cosβ + R(x, y, z)cosγ )dS.

<<< < Предыдущая 1 2 3 4 5 6 78 / 128 9 10 11 12 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
13.11.2019103.94 Кб2Практика МЭО.doc
#
04.05.20192.6 Mб2ПРАКТИКА ОД.doc
#
08.06.2015128.51 Кб6практика.doc
#
08.06.2015239.1 Кб9практика.doc
#
08.06.2015109.06 Кб20Практика_адвокат_заочка.doc
#
08.06.20151.69 Mб22Практикум з вищої математики.pdf
#
08.06.201519.22 Кб25Практическая 4.docx
#
03.08.2019214.53 Кб2Практична робота5.doc
#
07.05.2019326.14 Кб2Практичне занятт1.doc
#
08.06.201533.86 Кб85ПРИВАТНИЙ ВИЩИЙ НАВЧАЛЬНИЙ ЗАКЛАД.docx
#
11.11.2019264.7 Кб3программа по налоговой системе.doc