
Практикум з вищої математики
.pdf
§15. ФОРМУЛА СТОКСА
Основні теоретичні відомості
[1]– гл.ІХ, §2, с.491; [2] –глава 10, §4, с.628-630; [3]–глава ХV, §7, с.231, [4] – глава VII, §11, с.315-316, [5] – ч.ІІ, глава ІI, §6, с.56-66.
Формула Стокса встановлює зв’язок між поверхневими та криволінійними інтегралами.
z n 0
n 0
S
L
y
x
Нехай S – гладка орієнтована поверхня, а L – кусково-гладка замкнена крива, яка обмежує
Sі орієнтована відповідно до орієнтації поверхні
S(спостерігач розташований вздовж нормалі до обраної сторони поверхні, рухаючись по кривій L, буде бачити поверхню S зліва). І нехай функції P(x, y, z), Q(x, y, z), R(x, y, z) та їх
частинні похідні першого порядку неперервні на поверхні S , тоді має місце формула Стокса
∫P(x, y, z)dx + Q(x, y, z)dy + R(x, y, z)dz =
L
cosα
∂
= ∫∫ ∂x
S P(x, y, z)
або
cosβ |
cosγ |
|
||||
|
∂ |
|
∂ |
dS. |
||
|
|
|
|
|
|
|
|
∂y |
∂z |
||||
|
|
|
||||
Q(x, y, z) |
R(x, y, z) |
|
||||
∫P(x, y, z)dx + Q(x, y, z)dy + R(x, y, z)dz =
L
= |
|
∂R |
− |
∂Q |
|
∂P |
− |
∂R |
cosβ |
|
|
cosα + |
|
|
|||||
|
∫∫ |
|
|
|
|
|
|
|
|
|
S |
∂y |
|
∂z |
|
∂z |
|
∂x |
|
|
∂Q |
− |
∂P |
|
+ |
|
cosγ dS, |
||
|
∂x |
|
|
|
|
|
∂y |
|
|
де n0 = (cosα, cosβ, cosγ ) |
|
– одинична |
нормаль |
до |
вибраної сторони |
||||||||||
поверхні S . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Оскільки, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cosα dS = dydz, |
cosβ dS = dxdz, |
cosγ dS = dxdy, |
|||||||||||||
то формулу Стокса можна записати у вигляді |
|
|
|
|
|
||||||||||
∫P(x, y, z)dx + Q(x, y, z)dy + R(x, y, z)dz = |
|
|
|
||||||||||||
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
∂R |
− |
∂Q |
|
|
∂P |
− |
∂R |
|
|
∂Q |
− |
∂P |
|
|
|
|
dydz + |
|
|
|
dxdz + |
|
dxdy. |
||||||
|
∫∫ |
∂y |
|
∂z |
|
|
∂z |
|
|
|
|
|
∂x |
|
|
|
S |
|
|
|
|
∂x |
|
|
∂y |
||||||
Формула Стокса залишається в силі для кусково-гладких поверхонь, які можна розбити на частини, що взаємнооднозначно проектуються на всі координатні площини.
90

Питання для самоконтролю
1.Запишіть і доведіть формулу Стокса.
2.Що означає відповідність між орієнтацією поверхні та контуру, який її обмежує?
Зразки розв’язування задач
Приклад 1. Обчисліть криволінійний інтеграл
∫(z − 2y + x3)dx + (2x + z + y2)dy + (x + y + z4)dz ,
L
де L – крива перерізу циліндра x2 + y2 = Rx і сфери x2 + y2 + z2 = R2 при z ≥ 0 , у напрямі проти годинникової стрілки, якщо дивитися з додатного напряму осі Oz.
Розв’язання.
Скористаємось формулою Стокса:
P(x, y, z) = z − 2y + x3, Q(x, y, z) = 2x + z + y2, R(x, y, z) = x + y + z4. Знайдемо
∂P = −2, ∂P =1, |
|||
∂y |
∂z |
||
∂Q = 2, |
∂Q =1, |
||
∂x |
∂z |
||
∂R =1, |
∂R =1. |
||
∂x |
∂y |
||
|
|
|
|
В якості поверхні S оберемо частину сфери z = R2 + x2 + y2 , що |
|||
знаходиться в середині циліндра |
x2 + y2 = Rx . Проекцією цієї поверхні на |
|||||||||||||
|
2 |
|
2 |
|
|
R 2 |
+ y |
2 |
≤ |
R2 |
||||
площину Oxy буде круг D: x |
|
+ y |
|
≤ Rx |
x − |
|
|
|
|
. |
||||
|
|
|
|
|
||||||||||
|
|
|
|
|
|
2 |
|
|
|
4 |
|
|||
Отже, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫(z − 2y + x3)dx + (2x + z + y2)dy + (x + y + z4)dz = |
|
|
|
|
|
|
|
|||||||
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= ∫∫(2 + 2)dxdy + (1−1)dydz + (1−1)dxdz =4∫∫dxdy =πR2 , |
|
|
||||||||||||
S |
|
|
|
|
|
D |
|
|
|
|
|
|
|
|
оскільки, ∫∫dxdy– це площа круга радіуса |
R |
, яку знаходимо за формулою |
||||||||||||
2 |
||||||||||||||
D |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
πr2 при r = R . 2
91

Задачі для самостійного розв’язування
Обчисліть, користуючись формулою Стокса, криволінійний інтеграл по замкненому контуру L. Напрям на L відповідає додатному напряму його проекції на площину Oxy.
|
|
|
2 |
+ y |
2 |
= 4, |
|
|
|
|
|
|
|
|
|
|
|
|
|||
15.1. |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
∫zdx − ydz, L : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
L |
|
+ z = 5. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
2 |
+ y |
2 |
=1, |
|
|
|
|
|
|
|
|
|
|
15.2. |
∫xydx + yzdy + zxdz, |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
L : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
L |
|
|
|
|
|
|
+ y + z =1. |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
+ y |
2 |
+ z |
2 |
= 4, |
15.3. |
∫(z2 − x2 )dx − (x2 − y2)dy + (y2 |
+ z2 )dz, |
x |
|
|
|
|||||||||||||||
L : |
2 |
|
2 |
|
2 |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ y |
= z |
, z ≥ 0. |
|||
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|||
15.4. |
∫(x − 2z)dx + (x + 3y + z)dy + (5x + y)dz, L |
– контур трикутника ABC , |
|||||||||||||||||||
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
де A(1, 0, 0), |
B(0,1, 0), |
C(0, 0,1). |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
= 2(1− x |
2 |
− y |
2 |
), |
|
|
|
|
|
|
|
|||
15.5. |
∫ ydx + zdy + xdz, |
|
|
z |
|
|
|
|
|
|
|
|
|
||||||||
L : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
L |
|
|
|
|
|
= 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
15.6. ∫(y + z)dx + (z + x)dy + (x +
L
15.7. ∫(2x + y)dx − 2ydy, L –
L
A(0, −1), B(0, 2), C(2, 0) .
|
2 |
+ y |
2 |
+ z |
2 |
= a |
2 |
, |
|
x |
|
|
|
|
|
||||
y)dz, L : |
|
|
|
|
|
|
|
|
|
|
+ y + z = 0. |
|
|
|
|
||||
x |
|
|
|
|
|||||
контур |
|
трикутника |
|
ABC , |
де |
||||
|
|
|
|
|
|
|
|
|
|
|
x2 + y2 = a2, |
||||||||
15.8. |
∫(y − z)dx + (z − x)dy + (x − y)dz, |
|
|
|
|
|
|
|
|
|
|||||||||
L : |
|
|
|
|
|
y |
|
||||||||||||
|
L |
|
|
|
|
|
|
|
|
|
|
x |
+ |
=1 (a > 0, h > 0). |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
h |
|||||
|
|
|
2 |
+ y |
2 |
+ z |
2 |
= a |
2 |
, |
|
|
|||||||
15.9. |
∫ ydx + zdy + xdz, |
x |
|
|
|
|
|
|
|
|
|||||||||
L : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
L |
|
+ y + z = 0. |
|
|
|
|
|
|
|
|
|
|||||||
|
x |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
x |
+ y + z = 3, |
|
|
|
|
|
|
||||||||
15.10. ∫ y2dx + z2dy + x2dz, L : |
|
= 0, y = 0, z = 0. |
|||||||||||||||||
|
L |
|
|
x |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= x |
2 |
|
+ y |
2 |
−10, |
|
|
|
|
|
|
|
||||
15.11. ∫zdx − xdy + xdz, |
z |
|
|
|
|
|
|
|
|
|
|
||||||||
L : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
L |
|
= −1. |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
2 |
+ y |
2 |
+ z |
2 |
= R |
2 |
, |
|
|
|||||||
15.12. ∫ ydx + zdy + xdz, |
x |
|
|
|
|
|
|
|
|
||||||||||
L : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
L |
|
≥ 0, y ≥ 0, z ≥ 0. |
|
|
|
|
||||||||||||
|
x |
|
|
|
|
||||||||||||||
|
|
|
2 |
+ y |
2 |
+ z |
2 |
= 4, |
|
|
|
|
|
|
|||||
15.13. ∫ ydx − xdy + zdz, |
x |
|
|
|
|
|
|
|
|
|
|||||||||
L : |
2 |
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
||
|
|
|
+ y |
= z |
, z |
> 0. |
|
||||||||||||
|
L |
x |
|
|
|
|
|||||||||||||
92
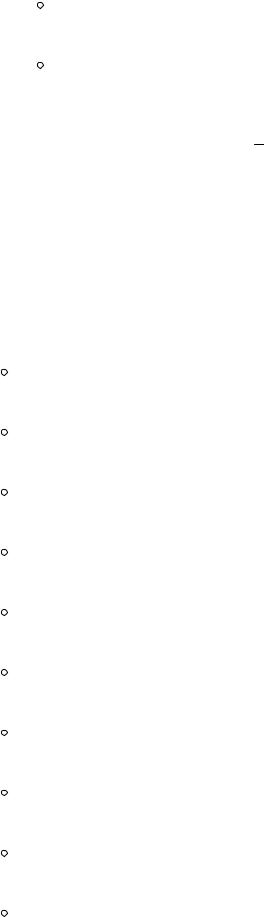
|
|
|
|
− x |
2 |
− z |
2 |
, |
||||
15.14. ∫ y |
2dx − x2dy + z |
y = 1 |
|
|
||||||||
2dz, L : |
|
|
|
|
|
|
|
|
|
|||
L |
|
|
|
|
|
≥ 0, z ≥ 0. |
||||||
|
x ≥ 0, y |
|||||||||||
|
|
|
2 |
+ y |
2 |
= R |
2 |
, |
|
|
||
15.15. ∫x |
|
x |
|
|
|
|
|
|||||
2 y3dx + dy + zdz, L : |
|
|
|
|
|
|
|
|
|
|
||
L |
|
|
= 0. |
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|||
Відповіді: 15.1. − 2π . 15.2. − π . 15.3. 0. 15.4. − 3. 15.5. − π . 15.6. 0. 15.7. 3. 15.8. − 2πa(a + h) . 15.9. − 
 3πa2. 15.10. − 27 . 15.11. 0.
3πa2. 15.10. − 27 . 15.11. 0.
15.12. − |
3πR2 |
. 15.13. − 4π . 15.14. − |
31 |
. 15.15. − |
1 |
πR |
6 . |
|
4 |
30 |
|
8 |
|||||
|
|
|
|
|
|
|||
Розрахункові завдання
Задача 19. Обчисліть за допомогою формули Стокса криволінійний інтеграл по замкненому контуру L. Напрям на L відповідає додатному напряму його проекції на площину Oxy.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
=12(x |
2 |
+ y |
2 |
), |
|
|
|
|
|
|
||||
1. |
∫ |
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|||||||||
(y + z)dx + (z + x)dy + (x + y)dz, L : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
= 24x + 2. |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
=10(x −1) |
2 |
+10y |
2 |
, |
|
|
|||||||||
2. |
∫ |
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|||||||||||||
(y − z)dx + (z − x)dy + (x − y)dz, L : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
L |
|
|
|
|
|
|
|
|
|
|
|
= 21− 20x. |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
2 |
+ y |
2 |
) + 3, |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
3. |
|
|
|
z = 8(x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
∫ y2dx + z2dy + x2dz, L : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z = 16y + 3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= 9(x |
2 |
+ y |
2 |
) +17, |
|
|
||||
4. |
∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|||||||
(x2 − yz)dx + (y2 − zx)dy + (z2 − xy)dz, L : |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= −36x +17. |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|||||||||||
|
|
|
|
= 9((x +1) |
2 |
+ y |
2 |
) − 7, |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
5. |
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
∫ ydx + zdy + xdz, L : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
L |
|
|
=18x +11. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
= 2(x |
2 |
|
+ y |
2 |
) |
−13, |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
6. |
∫x2 y3dx + dy + zdz, |
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
L : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
L |
|
|
|
= 8y −13. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3(x |
2 |
|
+ (y +1) |
2 |
), |
||
7. |
∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z = 2 − |
|
|
|
|
||||||||
(y2 − z2)dx + (z2 − x2)dy + (x2 − y2)dz, L : |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z = −6y − 4. |
|
|
|
||||||||||
|
|
|
|
|
= 3(x |
2 |
|
+ y |
2 |
|
) |
+ 7, |
|
|
|
|
|
|
|
|
|
|
|
|
||||
8. |
∫ |
(−ydx + xdy + 3dz), |
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
L : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
L |
|
|
|
=18x + 7. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
9.∫(x − 2z)dx
L
10. ∫xyzdx + (x
L
|
|
|
|
− 4((x +1) |
2 |
+ y |
2 |
), |
||
+ (x + 3y + z)dy + |
|
z = 5 |
|
|
||||||
(5x + y)dz, L : |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
z = 8x − 3. |
|
|
|
|
||||
|
|
|
2 |
+ y |
2 |
) +12, |
|
|
|
|
|
z =11(x |
|
|
|
|
|
|
|||
+ y + z)dy − x2 y2dz, L : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+12. |
|
|
|
|
|
|
|
z = −44x |
|
|
|
|
|
||||
93

|
|
|
|
|
|
|
|
|
|
|
|
|
= 5(x |
2 |
+ (y −1) |
2 |
) +1, |
|
|
|
|
|
|
|
||||||||||||||||
11. |
∫ ydx + (x −1)2 dy + zdz, |
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
L : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
L |
|
|
|
|
|
|
|
|
|
|
|
= −10x +11. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
=13(x |
2 |
+ y |
2 |
) −1, |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
12. |
∫x2 y3dx + dy + zdz, |
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
L : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
L |
|
|
|
|
|
|
|
|
= 52x −1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= 7((x +1) |
2 |
+ y |
2 |
) + 4, |
|||||
13. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|||||||||
∫(x + 3y + 2z)dx + (2x + z)dy + (x − y)dz, L : |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
=14x +18. |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
7(x |
2 |
+ y |
2 |
) −19, |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
14. |
|
|
|
|
|
z = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
∫ ydx − x)dy − 4dz, L : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z = 28x −19. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
3((x + 2) |
2 |
+ y |
2 |
) − 2, |
|
|
|||||||||
15. |
∫(x + y)dx + (x − z)dy + |
(y + z)dz, |
|
|
|
|
z |
|
|
|
|
|||||||||||||||||||||||||||||
L : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
=12x +13. |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
= 5(x |
2 |
+ y |
2 |
) |
+17, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
16. |
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
∫− ydx + xdy, L : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
L |
|
|
|
= 30x +17. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
+ y |
2 |
) + 5, |
|
|
|
|
|
|
|
|
|||||
17. |
|
|
|
|
|
|
|
|
z = 2((x − 3) |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
∫z2dx + x2dy + y2dz, L : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z = −12x + 25. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
+ y |
2 |
) −11, |
|
|
|
|
|
|
|
|
|
|
|||||||||||
18. |
∫z3dx + x3dy + y3dz, |
|
|
z = 8(x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
L : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z = 32x −11. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
= 5(x |
2 |
+ (y − 2) |
2 |
) − 8, |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
19. |
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
∫ y2dx + z2dz, L : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
L |
|
|
|
= −20x +17. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
= 4(x |
2 |
|
+ y |
2 |
) + 21, |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
20. |
∫ ydx − xdy + zdz, |
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
L : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
L |
|
|
|
|
|
|
= −16x + 21. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
+ (y + 3) |
2 |
) −1, |
|
|
|
|
|
|
|
|
|||||||||||||||
21. |
∫2xzdx − ydy + zdz, |
|
|
z = 4(x |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
L : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
z = 24x + 39. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
2 |
|
+ y |
2 |
) |
+ 9, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
22. |
∫z2dx, |
z = 3(x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
L : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
L |
|
|
|
|
+ 9. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
z = −12x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
7 − |
5(x |
2 |
+ y |
2 |
), |
|
|
|
|
|
|
|
|
|||||||||||
23. |
∫zy2dx + xz2dy + x2 ydz, |
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
L : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
=10x + 7. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
=13((x − |
2) |
2 |
+ y |
2 |
) − 5, |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
24. |
∫ ydx − xdy + zdz, |
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
L : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
L |
|
|
|
|
|
|
= −52x + 60. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
=17(x |
2 |
+ y |
|
2 |
) − 3, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
25. |
∫zdx + xdy + ydz, |
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
L : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
L |
|
|
|
|
|
|
= 68x − 3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
94
§16. ВЕКТОРНЕ ПОЛЕ. ВЕКТОРНІ ЛІНІЇ. ПОТІК І ДИВЕРГЕНЦІЯ ВЕКТОРНОГО ПОЛЯ
Основні теоретичні відомості
[1]– гл.ІХ, §3, с.496-522; [3]–глава ХV, §5-9, с.224-239, [4] – глава VIIІ, §2-3, с.333-338, [5] – ч.ІІ, глава ІI, §6, с.56-66.
Означення. Якщо кожній точці M області G поставлено у відповідність певний вектор a(M ), то кажуть, що в області G задано векторне поле a = a(M ), M G .
Приклади векторних полів
1. Поле швидкостей стаціонарного потоку рідини.
Нехай область G заповнено рідиною, яка в кожній точці M має певну швидкість v(M ), яка не залежить від часу (але змінюється від точки до точки), тоді маємо векторне поле швидкостей v = v(M ), M G .
2. Поле тяжіння.
Нехай в області G розподілено певну масу. Тоді на кожну матеріальну
точку M G діє гравітаційна сила F(M ). Отже, маємо векторне поле тяжіння F = F(M ), M G , яке називають гравітаційним.
3. Електростатистичне поле.
Нехай в області G задано деякий розподіл електричних зарядів, а в точці A простору розташований одиничний заряд. Тоді цей одиничний заряд діє на точку M із області G з певною силою Φ(M ) . Отже, маємо векторне
поле Φ = Φ(M ), M G , яке називають електростатистичним полем.
Якщо в просторі вибрана система координат Oxyz , то векторне поле a = a(M ) можна визначити, вказавши функції P(M ), Q(M ) та R(M ) – координати вектора a . Тобто
a(x, y,z) = P(x, y,z)i + Q(x, y,z) j + R(x, y,z)k = (P(x, y,z), Q(x, y,z), R(x, y,z)), де (x, y, z) – координати точки M у вибраній системі координат.
Зауваження. Надалі будемо вважати, що функції P(x, y, z), Q(x, y, z), R(x, y, z) мають неперервні частинні похідні в G .
Векторні лінії
Для наочного зображення векторних полів використовують векторні
лінії.
Означення. Векторною лінією векторного поля a називається така крива L, в кожній точці M якої дотична до неї має напрямок вектора поля
a(M0) |
|
|
|
a(M ) (рис. 1). |
|
|
|
|
|
a(M1) |
|
|
Нехай x = x(t), |
y = y(t) , |
z = z(t) |
|
|
a(M |
2 |
) |
– параметричні рівняння векторної лі- |
||
M |
1 |
M2 |
|
|
|
|
|
|
|
|
|
нії L поля a(M ), у векторному вигляді |
|||
M0 |
|
|
|
|
отримаємо: |
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 1 |
|
|
L: r(t) = x(t)i + y(t) j + z(t)k . |
||
|
|
|
|
|
|
|
|
95

Відомо, що вектор
dr = dxi + dyj + dzk = (dx,dy,dz)
напрямлений по дотичній до L. З означення векторної лінії випливає, що вектори a і dr колінеарні в кожній точці L. Тоді умови колінеарності
dx |
= |
dy |
= |
dz |
|
|
|
|
|||
P(x, y,z) |
Q(x, y,z) |
R(x, y,z) |
|||
|
|
являють собою систему рівнянь, що визначає векторні лінії поля.
Потік векторного поля
Нехай в області G простору Oxyz задано векторне поле
a(x, y, z) = P(x, y, z)i + Q(x, y, z) j + R(x, y, z)k
і деяку гладку або кусково-гладку двосторонню орієнтовану поверхню S . І нехай
n0 = cosα i + cosβ j + cosγ k
– вектор одиничної нормалі в довільній точці до поверхні S .
Означення. Потоком векторного поля a(M ) через поверхню S у напрямі нормалі n0 називається поверхневий інтеграл
Π = ∫∫np |
0 a dS = ∫∫ a, n0 |
|
dS = |
|
|
|
||
n |
|
|
|
|
|
|
|
|
S |
S |
|
|
|
|
|
|
|
= ∫∫(P(x, y,z)cosα + Q(x, y,z)cosβ + R(x, y,z)cosγ )dS. |
||||||||
S |
|
|
|
|
|
|
|
|
Π = ∫∫P(x, y,z)dydz + Q(x, y,z)dxdz + R(x, y,z)dxdy. |
||||||||
S |
|
|
|
|
|
|
|
|
або |
|
|
|
|
|
|
|
|
Отже, обчислення потоку векторного поля зводиться до обчислення |
||||||||
поверхневих інтегралів. |
|
|
|
|
|
|
|
|
Позначимо |
|
|
|
|
|
|
|
|
|
|
|
∂ |
|
∂ |
|
∂ |
|
|
= |
|
|
, |
|
, |
|
|
|
|
|
|
|||||
|
|
|
∂x |
|
∂y |
|
|
|
|
|
|
|
|
∂z |
|||
– символічний вектор, який називають оператором Гамільтона. Означення. Дивергенцією векторного поля
a(x, y, z) = P(x, y, z)i + Q(x, y, z) j + R(x, y, z)k
називається скаляр
∂P ∂Q ∂R
diva = ∂x + ∂y + ∂z = 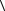 ,a
,a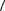 .
.
Потік векторного поля a через замкнену поверхню S можна обчислювати за формулою Остроградського-Гаусса:
∫∫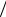 a, n0
a, n0 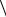 dS = ∫∫∫diva dV .
dS = ∫∫∫diva dV .
SG
96

Питання для самоконтролю
1.Дайте означення векторного поля.
2.Наведіть приклади векторних полів.
3.Запишіть диференціальні рівняння, що визначають векторні лінії.
4.Дайте означення потоку векторного поля через орієнтовану поверхню.
5.Що називають дивергенцією векторного поля?
6.Запишіть формулу Остроградського-Гаусса у векторній формі.
Зразки розв’язування задач
Приклад 1. Знайдіть векторні лінії векторного поля a = yi + j .
Розв’язання.
Векторні лінії даного поля визначаються диференціальними рівняння-
ми
dx = dy = dz.
y |
1 |
0 |
Це означає, що вектор (dx, dy, dz) |
колінеарний вектору (y,1, 0) . Звідси слі- |
|
дує, що dz = 0 z = C . Інтегруючи рівняння |
dx |
= |
dy |
dx = ydy , одержимо |
|||||||
|
|
||||||||||
1 |
|
|
|
|
|
y |
1 |
|
|||
|
|
|
|
|
|
|
|||||
|
y2 |
= x + C |
|
y2 |
= 2(x + C |
|
). |
||||
2 |
2 |
2 |
|||||||||
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|||
Отже, векторні лінії даного векторного поля визначаються системою рівнянь
|
2 |
= 2(x + C |
|
), |
y |
|
2 |
||
|
|
|
|
|
|
= C1. |
|
|
|
z |
|
|
||
Це параболи розташовані в площинах паралельних площині xOy.
Приклад 2. Обчисліть потік векторного поля a = 2i − j + 5zk через верхню сторону частини площини x + 2y + 3z − 6 = 0, що лежить в першому октанті.
Розв’язання.
Для даного векторного поля
P(x, y, z) = 2, Q(x, y, z) = −x, R(x, y, z) = 5z .
За означенням потоку векторного поля маємо
Π = ∫∫(2cosα − xcosβ + 5zcosγ ) dS .
S
Рівняння площини x + 2y + 3z − 6 = 0. Одиничний вектор нормалі до верхньої сторони площини має вигляд
|
n = 1 i + 2 j + |
3 k |
, |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
14 |
14 |
|
|
|
|
14 |
|
|
|
|
|
|
|
||||||||||
тобто |
cosα = |
|
1 |
|
, cosβ = |
|
|
2 |
|
, cosγ = |
|
3 |
|
. |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
14 |
14 |
||||||||||||||||||||||
|
14 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
97

Маємо
|
|
|
|
2 |
|
|
|
|
|
|
2x |
|
|
|
|
|
15z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
Π = ∫∫ |
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
dS |
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
14 |
14 |
14 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− x − 2y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
2x |
+ |
|
15 |
|
|
6 |
|
|
+ |
1 |
+ |
4 |
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
∫∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
dxdy |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
9 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
Dxy |
14 |
|
|
|
|
|
|
|
14 |
|
|
|
|
|
14 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3− |
1 |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
1 |
|
|
∫∫(32 − 7x −10y)dxdy = |
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
= |
|
|
|
∫dx |
|
|
|
∫(32 − 7x −10y)dy = |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
3 |
Dxy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
0 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
1 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3− |
1 |
x |
|
|
|
|
|
|
1 |
6 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
2 |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
= |
|
∫((32y − 7xy − |
5y2) |
|
|
|
|
2 )dx = |
|
|
|
∫ |
32 |
3− |
|
|
x |
− 7x 3 |
− |
|
x |
− 5 3 |
− |
|
|
|
x |
dx = |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
3 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
0 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
3 |
|
|
6 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
||||||
|
1 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
37x |
2 |
|
|
7x |
3 |
|
|
3 |
|
|
|
x |
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx = |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
||||||||||||||||||||||||||||
= |
|
96 |
− 37x + |
|
|
|
|
|
|
x |
|
|
− |
|
5 |
3− |
|
|
|
x |
|
|
|
|
96x − |
|
|
|
|
|
+ |
|
|
|
+10 |
|
|
|
|
|
|
|
|
|
= |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
3 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
6 |
|
|
|
|
|
3 |
|
|
|
|
|
|
|||||||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
= |
1 |
|
|
|
|
− |
1332 |
|
|
+ |
1512 |
|
− |
270 |
|
= 90. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
576 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
3 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
Приклад 3. Обчисліть потік векторного поля |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a = (x + z)i |
+ (z |
+ y)k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
через зовнішню сторону замкненої поверхні
S :{x2 + y2 = 9, z = 0, z = y (z ≥ 0)}.
Розв’язання.
Потік векторного поля a = (x + z)i + (z + y)k обчислимо за формулою Остроградського-Гаусса. Знайдемо дивергенцію даного векторного поля
|
z |
|
|
|
∂P ∂Q ∂R |
∂(x + z) |
|
∂0 |
∂(z + y) |
|
||
|
|
|
diva |
= |
∂x + |
∂y + ∂z = |
∂x |
|
+ |
∂y + |
∂z |
= |
|
|
|
|
=1+1= 2. |
|
|
|
|
|
|
||
|
|
|
Тоді шуканий потік знайдемо за формулою |
|
||||||||
|
|
|
|
|
Π = ∫∫∫diva dxdydz = 2∫∫∫dxdydz . |
|
||||||
0 |
|
|
|
|
|
G |
|
G |
|
|
|
|
3 |
3 |
y |
G – |
|
тіло, |
обмежене |
замкненою |
поверхнею |
||||
(рис.2) |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
S :{x2 + y2 = 9, z = 0, z = y (z ≥ 0)}. |
|
||||||||
|
x |
|
|
|
|
|||||||
|
Рис. 2 |
|
|
Перейдемо до циліндричних координат |
|
|||||||
|
|
|
|
|
||||||||
x = ρ cosϕ, y = ρ sinϕ, z = z , причому 0 ≤ϕ ≤ π , 0 ≤ ρ ≤ 3, 0 ≤ z ≤ y = ρ sinϕ .
98
Отримаємо:
π |
3 |
ρ sinϕ |
π |
|
3 |
π |
|
|
|
|
|
|
|
π0 = 36. |
|
Π = 2∫dϕ∫ρ dρ |
∫dz = 2∫sinϕ dϕ∫ρ 2dρ =18∫sinϕ dϕ = −18cosϕ |
|
|||||||||||||
|
|||||||||||||||
|
|||||||||||||||
0 |
0 |
0 |
0 |
|
0 |
0 |
|
|
|
|
|
|
|
|
|
|
Задачі для самостійного розв’язування |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
16.1. Обчисліть потік векторного поля |
a = (2z − x)i + (x + |
2z) j |
+ 3zk че- |
||||||||||||
рез |
верхню |
сторону |
трикутника, |
вирізаного |
|
із |
площини |
||||||||
x + 4y + z − 4 = 0 координатними площинами. |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
− |
|
|
|
||||
16.2. Знайдіть потік векторного поля a = (x − 2z)i + (3z |
4x) j + (5x + y)k |
||||||||||||||
через |
верхню |
сторону |
трикутника |
з |
|
вершинами |
|||||||||
A(1, 0, 0), |
B(0,1, 0), |
C(0, 0,1) |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
16.3. Знайдіть потік векторного поля a = x3i |
+ y3 j + z3k |
через зовнішню |
|||||||||||||
сторону бічної поверхні |
конуса |
x2 + y2 = |
R2 |
z2 |
між площинами |
||||||||||
|
|||||||||||||||
|
|
|
|
|
|
|
|
h2 |
|
|
|
|
|
|
|
z = 0, z = h. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
+ yk |
|
||||||
16.4. Знайдіть потік векторного поля a = (y − x)i + (x + y) j |
через зо- |
||||||||||||||
внішню |
сторону |
трикутника |
S , |
вирізаного |
|
із |
площини |
||||||||
x + y + z −1= 0 координатними площинами. |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
16.5. Знайдіть потік векторного поля a = i + yj + (1− z)k |
через зовнішню |
||||||||||||||
сторону бічної поверхні конуса z2 = x2 + y2 , що відтинається площинами z = 0, z = H .
16.6.Знайдіть потік векторного поля a = x2i + j + xzk через частину зовнішньої сторони параболоїда y = x2 + z2, що лежить в першому октанті і обмежену площиною y =1 (0 ≤ y ≤1).
|
|
|
|
|
16.7. Знайдіть потік векторного поля a = 2 |
− (2z −1)k через зов- |
|||
i |
+ 2yj |
|||
нішню сторону поверхні параболоїда |
x2 + y2 =1− 2z (z ≥ 0) розта- |
|||
шовану над площиною xOy. |
|
|
|
|
16.8.Знайдіть потік векторного поля a = i + (y + z) j + (z − y)k через зовнішню частину сферичної поверхні x2 + y2 + z2 = 9 , розташовану в першому октанті.
16.9.Знайдіть потік векторного поля a = (x − z)i + (z2 − y2) j + (x + z)k
через зовнішню сторону частини циліндричної поверхні x2 + y2 = R2, обмеженої площинами z = 0, z = b.
16.10.Знайдіть потік векторного поля a = 2 i − yj через зовнішню сторону частини циліндричної поверхні x2 + y2 = R2, x ≥ 0, y ≥ 0, 0 ≤ z ≤ H .
99
