Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Межрегианальная Академия Управления Персоналом

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Практикум з вищої математики

.pdf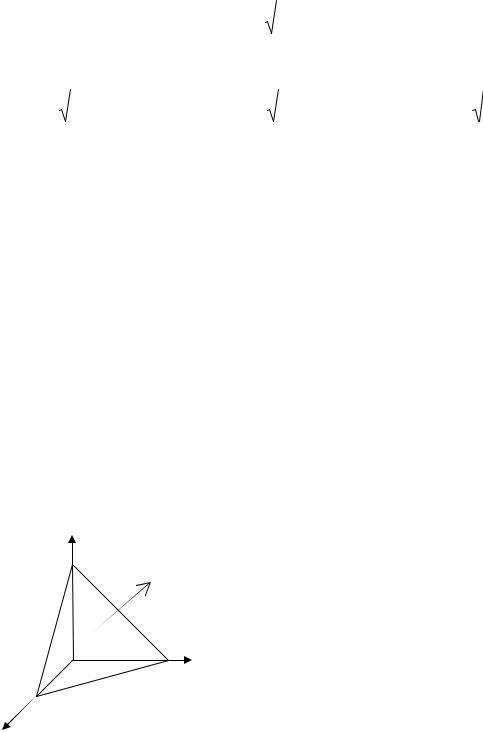

Скачиваний:

Добавлен:

08.06.2015

Размер:

1.69 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 89 / 129 10 11 12 > Следующая >>>

Зауваження. Якщо поверхня S задана рівнянням ϕ(x, y, z) = 0, то одиничний нормальний вектор до вибраної сторони поверхні визначається за формулою:

n0 = ±

ϕ′xi +ϕ′y j +ϕ′zk .

ϕ′ 2

+ϕ′ 2

Тобто напрямні косинуси даного вектора дорівнюють:

cosα =

± ϕ′x

, cosβ =

± ϕ′y

, cosγ =

± ϕ′z

ϕ′ 2

+ ϕ′ 2

ϕ′ 2

+ ϕ′ 2

ϕ′ 2

+ ϕ′ 2

Вибір знаку «+» чи «–» в цих формулах залежить від орієнтації поверхні.

Питання для самоконтролю

1.Дайте означення двосторонньої та односторонньої поверхні. Наведіть приклади.

2.Дайте означення поверхневого інтеграла ІІ роду.

3.Навдіть формули переходу від поверхневого інтеграла ІІ роду до подвійного інтеграла. Як при цьому визначається знак подвійного інтеграла?

Зразки розв’язування задач

Приклад 1. Обчисліть поверхневий інтеграл

∫∫(x +1)dydz ,

де S – верхня сторона трикутника, утвореного перетином площини x + y + z =1 з координатними площинами.

Розв’язання.

1 С

Тоді

∫∫(x +1)dydz =

	Нормальний вектор		n0	до	поверхні	S
n0	утворює гострий	кут з	віссю	Ox . Отже при
	переході до подвійного інтеграла маємо знак «+».
	Проектуємо	поверхню		S	з рівнянням
	x + y + z =1 на	координатну площину Oyz				в

1трикутник OBC .

B	y	Dyz : 0	≤ y ≤1, 0	≤ z ≤1− y .
		Dyz : 0	≤ y ≤1, 0	≤ z ≤1− y .
		Рівняння поверхні запишемо у вигляді
			x =1− y − z .
			1	1− y

∫∫(1− y − z +1)dydz = ∫∫(2 − y − z)dydz =∫dy ∫(2 − y − z)dz =

Dyz

0 0

1											2				1− y	1												2
															1− y
									z																	(1− y)
= ∫		2z − yz				−			z						dy = ∫		2(1		− y) − y(1− y) −							(1− y)				dy =
= ∫		2z − yz				−									dy = ∫		2(1		− y) − y(1− y) −											dy =
										2																	2
0										2						0											2
															0														1
															0
1													(1		− y)2					3			y3		(1	− y)3
= ∫	2 − 3y + y2									−						dy =		2y −			y	2 +		+						=
= ∫	2 − 3y + y2									−						dy =		2y −			y	2 +		+						=
															2					2			3			6
0															2					2			3			6			0
		3		1			1					2

= 2 −			+		−			=						.
= 2 −			+		−			=						.
		2	3			6					3

Приклад 2. Обчисліть поверхневий інтеграл

∫∫ydxdz ,

де S – верхня сторона параболоїда z = x2 + y2 при z ≤ 2.

Розв’язання.

Використаємо формулу

∫∫P(x, y, z)dydz + Q(x, y, z)dxdz + R(x, y, z)dxdy =

= ± ∫∫(P(x, y, z(x, y))(−z′x) + Q(x, y, z(x, y))(−z′y ) + R(x, y, z(x, y)))dxdy.

Dxy

Вданому поверхневому інтегралі

P(x, y, z) = 0, Q(x, y, z) = y, R(x, y, z) = 0 .

Проекцією поверхні S на площину Oxy			є область Dxy , обмежена колом
x2 + y2 = 2. З рівняння поверхні z′ = 2x,		z′		= 2y . Тому
	x	y
∫∫ydxdz =	∫∫y(−2y)dxdy = −2 ∫∫y2dxdy.
S	Dxy			Dxy

Перед подвійним інтегралом ставимо знак «+», так як, за умовою задачі вибирається верхня сторона параболоїда.

Переходячи до полярної системи координат, обчислюємо:

		2π			2						2π			2
− 2 ∫∫y2dxdy = −2 ∫dϕ ∫							ρ3 sin2 ϕ dρ = −2 ∫					sin2 ϕ dϕ ∫			ρ3dρ =
Dxy		0		0							0		0

				4				2		2π								2π
								2
2π			ρ
= −2 ∫	sin	2 ϕ	ρ						dϕ = − ∫		(1− cos2ϕ)dϕ =		−ϕ +			1	sin2ϕ	= −2π.
= −2 ∫	sin	2 ϕ							dϕ = − ∫		(1− cos2ϕ)dϕ =		−ϕ +				sin2ϕ	= −2π.
0			4			0				0					2			0
0										0								0

Задачі для самостійного розв’язування

Обчисліть поверхневі інтеграли другого роду.

13.1.

∫∫(x2 + y2)dxdy, де

–

зовнішня

сторона

частини параболоїда

z =1− x2 − y2 , яка розміщена над площиною Oxy.

13.2.

∫∫zdxdy, де S – зовнішня сторона сфери x2 + y2 + z2 =1.

13.3

∫∫(y − z)dydz ,

де

–

зовнішня

сторона

конічної

поверхні

z2 = x2 + y2 (0 ≤ z ≤ 2).

13.4.

∫∫(xy −1)dxdz ,

де

–

зовнішня

сторона тетраедра, обмеженого

площинами 3x − y + z = 3,

x = 0,

y = 0,

z = 0.

13.5.

∫∫xyzdxdy , де

– зовнішня сторона параболоїда

z = x2 + y2, що

відтинається площиною z =1.

13.6.

∫∫xdydz + ydxdz + zdxdy ,

де

–

зовнішня

сторона

сфери

x2 + y2 + z2 = R2.

13.7.

∫∫(y − z)dydz + (z − x)dxdz + (x − y)dxdy ,

де S

–

зовнішня

сторона

конічної поверхні z2 = x2 + y2

(0 ≤ z ≤ a).

13.8.

∫∫2dxdy + ydxdz − x2zdydz ,

де

–

зовнішня

сторона

частини

еліпсоїда 4x2 + y2 + 4z2 = 4, x ≥ 0, y ≥ 0,

z ≥ 0.

13.9.

∫∫ ydydz + xdxdz + zdxdy,

де

–

зовнішня

сторона трикутника,

утвореного при перетині

площини

x − y + z =1

координатними

площинами.

13.10. ∫∫x2dydz + y2dxdz + z2dxdy,

де

–

зовнішня

сторона

сфери

(x − a)2 + (y − b)2 + (z − c)2 = R2 .

13.11. ∫∫(x2 + y2 )dxdy , де

–

зовнішня

сторона

конічної

поверхні

z = x2 + y2 (0 ≤ z ≤ 2).

13.12. ∫∫z2dxdy , де	S	–	зовнішня			сторона	півсфери x2 + y2 + z2 = 9
S
(z ≥ 0).
13.13. ∫∫(3x − y)dxdz,	де S		–	верхня		сторона	трикутника, вирізаного із
S
площини 2x + y − z = 4 координатними площинами.
13.14. ∫∫(x2 − xy)dxdy ,		де	S	–	зовнішня сторона конічної поверхні
S
x2 + y2 = z2 (0 ≤ z ≤1).
13.15. ∫∫xzdxdy + xydydz + yzdxdz ,					де	S – зовнішня сторона трикутника,

вирізаного із площини x + y + z =1 координатними площинами.

13.16. ∫∫x2 y2zdxdy , де S – зовнішня сторона верхньої половини сфери

x2 + y2 + z2 = R2.

13.17. ∫∫zdxdy, де S – зовнішня сторона еліпсоїда

=1.

13.18. ∫∫ yzdxdy + xzdydz + xydxdz ,

де

–

зовнішня

сторона

поверхні,

розташованої в першому октанті і такої, що складається із циліндра

x2 + y2 = H 2 та площин x = 0,

y = 0,

z = 0, z = H .

13.19. ∫∫ y2zdxdy + xzdydz + x2 ydxdz ,

де

–

зовнішня

сторона

поверхні,

розташованої в першому октанті і складеної із параболоїда

обертання

z = x2 + y2,

циліндра

x2 + y2 =1

площин

x = 0, y = 0, z = 0, z = H .

13.20. ∫∫xdydz + ydxdz + zdxdy, де

S – зовнішня сторона куба, утвореного

площинами x = 0, y = 0,

z = 0, x =1,

y =1, z =1.

Відповіді: 13.1. π . 13.2.

π . 13.3. −

13.4.

. 13.5. 0. 13.6. 4πR3.

13.7. 0. 13.8.

13π

. 13.9. −

. 13.10.

πR2(a + b + c) . 13.11. 8π .

13.12.

81π

. 13.13. 0.

13.14. π . 13.15.

. 13.16.

πR7 . 13.17. 32π .

105

πH

13.18. R

. 13.19.

. 13.20. 3.

Розрахункові завдання

Задача 17. Обчисліть поверхневі інтеграли ІІ роду.

∫∫x2dydz , де S – нижня сторона півсфери z =

1− x2 − y2 .

∫∫x2dydz, де S – верхня сторона півсфери z =

4 − x2 − y2 .

∫∫(x2 + y2)dxdy,

де S

–

верхня

сторона півсфери

x2 + y2 + z2 =16

(z ≥ 0).

∫∫x2dxdz, де S – верхня сторона еліпсоїда y = b 1−

−

∫∫(x2 + y2)dydz ,

де S

–

нижня

сторона циліндра

x2 + y2 = 4

між

площинами z = 0, z = 2.

∫∫ ydxdz , де

–

верхня

сторона

площини

x + y + z = 2

між

координатними площинами x = 0,

y = 0, z = 0.

∫∫(y2 + z2)dydz ,

де S

–

верхня

сторона параболоїда

x = 4 − y2 − z2 ,

розміщена над Oyz.

∫∫z2dxdy , де S – зовнішня сторона еліпсоїда x2 + y2 + 2z2 = 2.

∫∫ yzdydz + xzdxdz, де

– верхня

сторона

площини

x + 2y + z = 4,

розташована між координатними площинами.

10.

∫∫zdxdy, зовнішня сторона еліпсоїда

11.

∫∫x2dydz, де S – зовнішня сторона сфери x2 + y2 + z2 = 4.

z =1− (x2 + y2 ), розташована

12.

∫∫zdxdy, де S

– верхня частина поверхні

над площиною xOy.

13.

∫∫(2x + y)dydz + (x − 2)dxdy,

де

–

верхня

сторона площини

x + y − 2z − 2 = 0, розташована між координатними площинами.

18. ∫∫

14. ∫∫x2 + y2dxdy , де S – верхня сторона півсфери z = 9 − x2 − y2 .

15. ∫∫(y2 + z2)4 + y2 + z2dydz, де S – зовнішня сторона поверхні

параболоїда 4x = y2 + z2 , що відтинається площиною x = 4.


		x2	+ y2dxdy
		x2	+ y2dxdy		2 − x	2 − y	2 .
16.	∫∫			, де S – верхня сторона півсфери z = R


	S R2		− x2 − y2
17.	∫∫(x + y)dydz + (y + z)dxdy , де S – верхня сторона трикутника,

вирізаного із площини 3x + y + 3z − 3 = 0 координатними площинами.

dxdz , де S – зовнішня частина циліндричної поверхні

S x2 + y2

x2 + y2 = 9, розміщена між площинами z = 0, z = 4.

19.

∫∫(2y − z)dydz + (z − x)dxdz ,

де

–

верхня

сторона трикутника,

вирізаного із площини 2x − y + z = 2 координатними площинами.

20.

∫∫(9 + y2 + z2 )dydz , де

– зовнішня сторона параболоїда 6x = y2 + z2,

що відтинається площиною x = 6.

21.

∫∫(y − z)dydz + (x − y)dxdy, де S

– зовнішня сторона конічної поверхні

x2 = y2 + z2, 0 ≤ x ≤ 2.

∫∫

dydz

dxdz

dxdy

22.

, де S – зовнішня сторона сфери x2 + y

2 + z2 = 4.

23.

∫∫x2dydz + y2dxdz,

де

–

верхня

сторона

конуса z = 2 −

x2 + y2 ,

розташована над площиною xOy.

24.

∫∫

dxdy

де

–

верхня

сторона

частини

півсфери

S R2 − x2 − y2

z =

R2 − x2 − y2 , розташованої в циліндрі x2 + y2 = Rx .

25.

∫∫

ydxdy

, де

–

зовнішня

сторона

циліндричної

поверхні

Rx − x2

x2 + y2 = Rx , розташованої в середині сфери x2 + y2 + z2 = R2.

§14. ФОРМУЛА ОСТРОГРАДСЬКОГО-ГАУССА

Основні теоретичні відомості

[1]– гл.ІХ, §2, с.494-496; [2] –глава 10, §4, с.626-628; [3]–глава ХV, §8, с.233236, [4] – глава VII, §11, с.315, [5] – ч.ІІ, глава ІI, §6, с.56-66.

Формула Остроградського-Гаусса стосується замкнених просторових областей і пов’язує потрійний інтеграл по області G R3 з поверхневим інтегралом по зовнішній стороні поверхні S , яка обмежує цю область.

Нехай

– кусково-гладка поверхня,

яка

обмежує

тіло G , а

P(x, y, z),

Q(x, y, z), R(x, y, z)

– неперервні разом з частинними похідними

∂P

∂Q

∂R

∂x

, ∂y ,

∂z

області

G функції. Тоді справедлива формула

Остроградського-Гаусса

∫∫

P(x, y, z)dydz + Q(x, y, z)dxdz + R(x, y, z)dxdy =

∂P

∂Q

∂R

∫∫∫

∂x

∂y

dxdydz .

∂z

Питання для самоконтролю

1. Запишіть і доведіть формулу Остроградського-Гаусса.

Зразки розв’язування задач

Приклад 1. Обчисліть поверхневий інтеграл

∫∫x3dydz + y3dxdz + z3dxdy,

де S – зовнішня сторона сфери x2 + y2 + z2 = a2.

Розв’язання.

Використовуючи формулу Остроградського-Гаусса, знаходимо:

P(x, y, z) = x3, Q(x, y, z) = y3, R(x, y, z) = z3,

∂P = 3x2,	∂Q = 3y2,	∂R = 3z2.
∂x	∂y	∂z

I = ∫∫x3dydz + y3dxdz + z3dxdy = 3∫∫∫(x2 + y2 + z2)dxdydz.

	S					G
Перейдемо до сферичних координат:
	x = rsinθ cosϕ,
	y = rsinθ sinϕ,		0 ≤ r ≤ a, 0 ≤ ϕ < 2π ,				0 ≤θ ≤ π ,
	z = rcosθ,
Одержимо:
π	2π a			3a5 π		2π		6πa5
I = 3∫sinθ dθ ∫dϕ ∫r4dr =					∫sinθ dθ	∫dϕ = −
I = 3∫sinθ dθ ∫dϕ ∫r4dr =				5	∫sinθ dθ	∫dϕ = −		5
0	0	0		5	0	0		5
0	0	0			0	0

J= r2 sinθ .

π12πa5 cosθ 0 = 5 .

Задачі для самостійного розв’язування

Використовуючи формулу Остроградського-Гаусса, обчисліть поверхневі інтеграли.

14.1.	∫∫xzdydz + x2 ydxdz + y2zdxdy , де S – зовнішня сторона поверхні, що
	S
	розташована в 1-му октанті і складається з параболоїда обертання
	z = x2 + y2, циліндра x2 + y2 =1 і координатних площин.
14.2.	∫∫x2dydz + 3ydxdz − 2xzdxdy ,		де	S –		зовнішня		сторона		піраміди,
	S
	обмеженої площинами x = 0,		y = 0, z = 0, x + y + z −1= 0.
14.3.	∫∫xdydz + ydxdz + (1− z)dxdy,		де		S	–	зовнішня		сторона		повної
	S
	поверхні конуса z2 = x2 + y2, 0 ≤ z ≤ H .
14.4.	∫∫x2dydz + xdxdz + xzdxdy ,	де		S	–	зовнішня		сторона		поверхні
	S
	y = x2 + z2, x = 0, y =1, z = 0, (x ≥ 0).
14.5.	∫∫2xdydz − ydxdz + zdxdy, де		S		–	зовнішня		сторона		поверхні
	S
	9 − z = x2 + y2, 0 ≤ z ≤ 9 .
14.6.	∫∫yzdydz − xdxdz − ydxdy,	де		S –		зовнішня		сторона			конуса
	S
	y2 = x2 + z2, y = 0, y =1.
14.7.	∫∫x2dydz + y2dxdz + z2dxdy,		де		S	–	зовнішня		сторона		куба
	S
	0 ≤ x ≤ a, 0 ≤ y ≤ a, 0 ≤ z ≤ a .
14.8.	∫∫x2dydz + y2dxdz + z2dxdy,		де	S	–	зовнішня		сторона		піраміди,
	S
	обмеженої площинами x = 0,		y = 0, z = 0, x + y + z =1.
14.9.	∫∫x3dydz + y3dxdz + 4zdxdy,	де		S	–	зовнішня		сторона		поверхні,
	S
	обмеженої параболоїдом 2z = x2 + y2 і площини z = 2.
14.10. ∫∫5xdydz + 3ydxdz + 2zdxdy ,			де		S		– зовнішня			поверхня
	S
	паралелепіпеда,		обмеженого						площинами

x = 0, x =1, y =1, y = 2, z = 2, z = 3.

14.11. ∫∫(3z − 2)dxdy, де S – зовнішня поверхня сфери x2 + y2 + z2 = 9 .

Відповіді: 14.1.	π	. 14.2.	1	. 14.3.	πH	3	. 14.4.	2	. 14.5.	8	. 14.6.	0.

	8		2		3			5		π

14.7. 3a4. 14.8. 1 . 14.9. 32π . 14.10. 10. 14.11. 108π . 4

Розрахункові завдання

Задача 18. Обчисліть поверхневі інтеграли через зовнішню сторону замкненої поверхні S , що обмежує тіло G , за допомогою формули Остроградського-Гаусса.

+ y

= 9,

∫∫(x + 2z)dydz − (y − z)dxdy,

S :

z = x, z = 0 (z ≥ 0).

= x

+ y

+1,

∫∫2xdydz + zdxdy,

S :

+ y

= 4, z = 0.

= x

y = 4x

y =1 (x ≥ 0),

∫∫2xdydz + 2ydxdz + zdxdy,

S :

= y,

z = 0.

= 6

− x

− y

∫∫3xdydz − zdxdz,

S :

= x

+ y

, (z ≥ 0).

= x

+ z

∫∫(z + y)dydz + ydxdz − 3dxdy,

S :

= 2.

+ y

=1,

z = 0,

∫∫xdydz − (2x + 3y)dxdz + ydxdy,

S :

x + 2y + 3z = 6.

+ y

+1, z = 0,

∫∫2(z − y)dxdz + (x − z)dxdy,

z = x

S :

+ y

=1.

= 4 − 2(x

+ y

∫∫xdydz + zdxdz − ydxdy, S :

= 2(x

+ y

= x

+ y

∫∫zdydz − 4ydxdz + 2xdxdy,

S :

=1.

3x + 2y =12,

∫∫4xdydz − 2ydxdz − zdxdy,

y = 0,

10.

S : 3x + y = 6,

+ y + z = 6, z = 0.

+ y =1, x = 0, y = 0,

11.

∫∫8xdydz − 8ydxdz + xdxdy,

S :

= x

+ y

, z = 0.

12. ∫∫

		2	+ y	2	,
4z = x			+ y		,
zdydz + xdxdz − zdxdy, S :
	= 4.
z	= 4.

−

2(x

+ y

∫∫6xdydz − 2ydxdz − zdxdy,

z = 3

13.

S :

= x

+ y

, (z ≥ 0).

+ 4y

= 4,

14.

∫∫(z + y)dydz + (x − z)dxdz + zdxdy, S :

+ 4y + z =12, z =1.

3z = 27 − 2(x2 + y2),

∫∫(y + 2z)dydz + (2 − y)dxdz + 3xdxdy,

15.

S :

= x

+ y

, (z ≥ 0).

= x, y = 2x, x = 2,

∫∫(y + 6x)dydz + (5x + 2y)dxdz + 4ydxdy,

16.

S :

= x

+ y

, z = 0.

+ y

=1,

17.

∫∫ydydz + 5ydxdz + zdxdy,

S :

= x, z = 0 (z ≥ 0).

+ y

=1,

18.

∫∫zdydz + (3y − z)dxdz − zdxdy, S :

+ y

+ 2, z = 0.

z = x

+ y

= 2x,

∫∫ydydz + (x + 2y)dxdz + xdxdy,

19.

S :

+ y

, z

= 0.

z = x

y =

2x, y = 2, x =1,

∫∫(x + y + z)dydz + (2x − x)dxdz + (3z + y)dxdy,

20.

S :

+ y

, z = 0.

z = x

+ y

∫∫7xdydz + zdxdz + (x − y + 5z)dxdy,

z = x

21.

S :

z = 2y.

− y

∫∫(x + z)dydz + ydxdy,

z = 8− x

22.

S :

+ y

z = x

23. ∫∫(2y

24. ∫∫(2y

25. ∫∫(3x

		2	+ y	2		=1,
	x		+ y			=1,
− 3z)dydz + (3x + 2z)dxdz + (x + y + z)dxdy, S :
		= 4 − x − y, z = 0.
	z	= 4 − x − y, z = 0.
z	= x2		+ y2 +1, z = 0

−15x)dydz + (z − y)dxdz − (x − 3y)dxdy, S :	2 + y		2 =		1
x					1	.
x						.
				4

	2	+ y	2	,
z = x		+ y		,
− y − z)dydz + 3ydxdz + 2zdxdy, S :

z 2y.

<<< < Предыдущая 1 2 3 4 5 6 7 89 / 129 10 11 12 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
13.11.2019103.94 Кб2Практика МЭО.doc
#
04.05.20192.6 Mб2ПРАКТИКА ОД.doc
#
08.06.2015128.51 Кб6практика.doc
#
08.06.2015239.1 Кб9практика.doc
#
08.06.2015109.06 Кб20Практика_адвокат_заочка.doc
#
08.06.20151.69 Mб22Практикум з вищої математики.pdf
#
08.06.201519.22 Кб25Практическая 4.docx
#
03.08.2019214.53 Кб2Практична робота5.doc
#
07.05.2019326.14 Кб2Практичне занятт1.doc
#
08.06.201533.86 Кб85ПРИВАТНИЙ ВИЩИЙ НАВЧАЛЬНИЙ ЗАКЛАД.docx
#
11.11.2019264.7 Кб3программа по налоговой системе.doc