
Практикум з вищої математики
.pdf
5. |
∫∫∫(x + 2y)dxdydz; |
G : z = 4x2 + 3y2, |
y = x, y = 0, |
z = 0, z = 2 . |
||||||||||||||||
|
G |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6. |
∫∫∫(x2 + y2 + z2)ydxdydz ; |
G : x = 0, x = a, y = 0, y = b, z = 0, z = c. |
||||||||||||||||||
|
G |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7. |
∫∫∫(2x + 3y − z)dxdydz ; G : x + y = k, x = 0, y = 0, z = 0, z = a (k > 0,a > 0). |
|||||||||||||||||||
|
G |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8. |
∫∫∫ xyzdxdydz; |
G : x + y + z =1, |
x = 0, |
y = 0, z = 0. |
|
|||||||||||||||
|
G |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9. |
∫∫∫ |
|
dxdydz |
|
|
|
|
; G : |
x |
+ |
y |
|
+ |
z |
=1, x = 0, y = 0, |
z = 0 . |
||||
|
|
|
|
|
|
|
|
3 |
|
|
|
|||||||||
|
G |
x |
|
y |
|
|
z |
2 |
4 |
|
3 |
|
|
|
||||||
|
|
1+ |
|
+ |
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|||
10. |
∫∫∫xyzdxdydz; |
G : z = x2 + 2y2, |
x = 0, |
y = 0, z = 4. |
|
|||||||||||||||
|
G |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11.∫∫∫xdxdydz ; G : y2 = 3z, x2 + y2 = 4, z = 0. G
12. |
∫∫∫(x + y)dxdydz ; G : y2 = 4x, x + 2y + z = 5, |
y = 0, z = 0. |
||||||
|
G |
|
|
|
|
|
||
13. |
∫∫∫xdxdydz ; G : x = |
y2 |
+ |
z2 |
=1, x = 2, y = 0, |
z = 0. |
||
4 |
|
|||||||
|
G |
2 |
|
|
||||
|
|
|
|
|
|
|||
14. |
∫∫∫x |
|
ydxdydz ; G : z = 4 − x2 , z = 0y = 0, y = 5, x = 0 . |
|||||
|
||||||||
|
G |
|
|
|
|
|
||
15.∫∫∫ yzdxdydz ; G :6x − 9y + 5z = 0, 3x − 2y = 0,4x − y = 0,x + y = 5,z = 0. G
16.∫∫∫(x + y + z)dxdydz; G :2x + y − 2 = 0, 4x + 3y − 2z = 0,x = 0, y = 0,z = 0.
G
17.∫∫∫xyzdxdydz; G :z = 9 − x2,x + y = 3, y = 2x,z = 0, y = 0 . G
18.∫∫∫x2 yzdxdydz; G :z2 = xy,x + y =1,x = 0, y = 0,z = 0. G
19.∫∫∫(y − x2)dxdydz ; G : z = 
 xy, x + y =1,z = 0. G
xy, x + y =1,z = 0. G
20.∫∫∫x2 yexyzdxdydz ; G :x = 0, y = 0,z = 0,x =1, y =1,z =1. G
30

21.∫∫∫xdxdydz ; G :x = 0, y = 0,z = 0, y = h,x + z = a(a > 0,h > 0). G
22. ∫∫∫(x2 + y2 + z2)ydxdydz ; G :2x + 3y + 4z =12,x = 0, y = 0, z = 0 .
G |
|
|
|
23. ∫∫∫ yxdxdydz; G :z = 4 − y |
2, y = |
x2 |
,x = 0, z = 0. |
|
|||
G |
2 |
|
|
|
|
|
|
xdxdydz
Gz2 ; G :2z = x ,3x + 2y =12, y = 0,z = 0 .
25.∫∫∫(2x + 3y + z)dxdydz ; G :x = 2 − y2,z = 4, x = 0, y = 0,z = 0 .
G2
§5. ЗАМІНА ЗМІННОЇ В ПОТРІЙНОМУ ІНТЕГРАЛІ
Основні теоретичні відомості
[1] – гл.VIII,§1, с.434-440; [2] – гл.10,§1, с.589-592; [3] – глава ХІV, §1-3, с.196-199; [4] – глава VII, §1, с.286-293; [5] – глава I, §1, с.23-28.
Розглянемо потрійний інтеграл ∫∫∫ f (x, y, z)dxdydz, де |
функція |
G |
|
f (x, y,z) неперервна в просторовій області G . Нехай область G |
простору |
Oxyz пов’язана взаємнооднозначною відповідністю з областю G ' простору O 'uvw за допомогою формул:
x = x(u,v, w), y = y(u,v, w), z = z(u,v, w),
де x(u,v, w), y(u,v, w), |
z(u,v, w) неперервні і мають частинні похідні 1-го |
|||||||
порядку по змінних u, v, |
w в області G '. |
|
|
|
|
|
||
Означення. Визначник |
|
|
|
|
|
|
|
|
|
|
∂x |
∂x |
∂x |
|
|
||
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
∂u |
∂v |
∂w |
|
|
||
|
J(u,v,w) = |
∂y ∂y ∂y |
|
|
||||
|
∂u |
|
∂v |
∂w |
|
|
|
|
|
|
|
|
|||||
|
|
∂z |
∂z |
∂z |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
∂u |
∂v |
∂w |
|
|
||
називають якобіаном даного відображення.
Теорема. Якщо J(u,v,w) ≠ 0 в області G ', то має місце формула заміни змінних у потрійному інтегралі:
∫∫∫ f (x, y, z)dxdydz = ∫∫∫ f (x(u,v, w), y(u,v, w), z(u,v, w)) J(u,v,w) dudvdw.
G G '
31
На практиці найчастіше використовуються циліндричні та сферичні координати.
z
M(x,y,z)
z
ρ
y
x
ϕ x
y
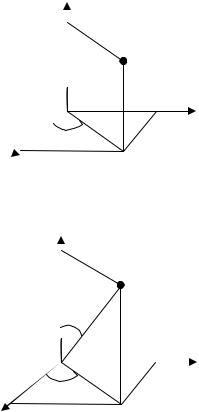
1) Циліндричні координати ρ, ϕ, z пов’язані з декартовими x, y, z співвідношеннями:
x = ρ cosϕ,y = ρ sinϕ,
z = z,
0 ≤ ρ < +∞, 0 ≤ ϕ < 2π , − ∞ < z < +∞, оскільки J = ρ , то має місце така формула:
∫∫∫ f (x, y, z)dxdydz = ∫∫∫ f (ρ cosϕ, ρ sinϕ, z)ρdρdϕdz.
G G '
z
|
|
M(x,y,z) |
|
θ |
ρ |
|
|
z |
|
ϕ |
y |
x |
x |
|
y |
|
|
|
|
2) Сферичні координати r, ϕ, θ , пов’язані з декартовими x, y, z співвідношеннями:
x = rsinθ cosϕ,
= sinθ sinϕ,
y r
z = rcosθ,
0 ≤ r < +∞, 0 ≤ ϕ < 2π , 0 ≤θ ≤ π ,
J = r2 sinθ , тому має місце формула:
∫∫∫ f (x, y, z)dxdydz = ∫∫∫ f (rsinθ cosϕ, rsinθ sinϕ, rcosθ )r2 sinθdrdϕdθ.
G |
G ' |
Зауваження. До циліндричних координат буває доцільно переходити, якщо область інтегрування є круговим циліндром, прямолінійні твірні якого паралельні осі Oz. Рівняння такого циліндра в сферичних координатах
ρ = const.
Переходити до сферичних координат зручно, коли область інтегрування є куля (рівняння її межі x2 + y2 + z2 = R2 у сферичних координатах має вигляд ρ = R) або його частина, а також якщо підінтегральна функція має вигляд f (x2 + y2 + z2 ).
Питання для самоконтролю
1.Дайте означення якобіана відображення.
2.Сформулюйте теорему про заміну змінних у потрійному інтегралі.
3.Чому дорівнює якобіан в циліндричних координатах.
4.Як знаходяться межі інтегрування для потрійного інтеграла в циліндричних координатах? Наведіть приклад області, для якої межі інтегрування в циліндричних координатах сталі.
5.Чому дорівнює якобіан у сферичних координатах.
6.Як знаходяться межі інтегрування для потрійного інтеграла у сферичних координатах? Наведіть приклад області, для якої межі інтегрування у сферичних координатах сталі.
32
Зразки розв’язування задач
Приклад 1. Обчисліть ∫∫∫zdxdydz , якщо область G обмежена коні-
G
чною поверхнею z2 = x2 + y2 і площиною z = 2. |
|
|
|
|
|
||||||||||||||||||
Розв’язання. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
z |
|
|
|
Дане тіло, обмежене знизу конусом z2 = x2 + y2, а |
||||||||||||||||||
|
|
|
|
зверху площиною |
|
z = 2. Його проекцією на площину |
|||||||||||||||||
|
2 |
|
|
Oxy є круг |
x |
2 |
+ y |
2 |
≤ 4 . Використаємо циліндричні ко- |
||||||||||||||
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
ординати. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
O |
y |
|
|
Рівняння заданого конуса в циліндричних коорди- |
||||||||||||||||||
|
|
натах набуде вигляду |
z = ρ ; а рівняння кола, що обме- |
||||||||||||||||||||
2 |
|
|
|||||||||||||||||||||
|
|
|
|||||||||||||||||||||
|
|
|
жує проекцію, ρ = 2. Отже маємо: |
|
|
|
|
||||||||||||||||
x |
|
|
|
|
|
|
|
||||||||||||||||
|
2π |
|
2 |
2 |
|
2π |
|
2 |
|
|
z |
2 |
2 |
|
|
|
|
|
|
|
|
||
∫∫∫zdxdydz = ∫ |
dϕ ∫ρdρ ∫zdz = ∫ |
dϕ ∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
ρ |
2 |
dρ = |
|
|
|
|
|
||||||||||||||||
|
0 |
|
0 |
ρ |
|
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
||||
G |
|
|
|
|
|
|
|
ρ |
|
|
|
|
|
|
|
|
|||||||
2π 2 |
|
2 |
2π 2 |
|
|
|
|
|
3 |
|
|
|
2π |
|
|
|
4 |
|
2 |
|
2π |
||
|
|
|
|
|
|
|
|
ρ2 − ρ |
|
|
|||||||||||||
= ∫ dϕ∫ρ(2 − ρ |
)dρ = ∫ |
dϕ∫ |
2ρ − ρ |
|
dρ = ∫ |
|
|
|
|
|
dϕ = 2 |
∫dϕ = 4π. |
|||||||||||
0 |
0 |
2 |
0 |
|
|
|
|
2 |
|
|
|
0 |
|
|
8 |
|
|
|
0 |
||||
0 |
|
|
|
|
|
|
|
0 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Приклад 2. |
Обчисліть |
∫∫∫x2dxdydz , |
|
якщо |
|
область |
G – куля |
||||||||||||||||
G
x2 + y2 + z2 ≤ R2 .
Розв’язання.
Перейдемо до сферичних координат. У даному випадку координати ρ, ϕ, θ будуть змінюватися так:
0 ≤ ρ ≤ R, 0 ≤ϕ < 2π , 0 ≤θ ≤π .
Отже,
|
|
|
|
|
|
|
|
|
|
π |
|
π |
R |
|
|
|
∫∫∫x2dxdydz = ∫∫∫ρ 4 sin3 |
θ cos2ϕdρdϕdθ = = ∫sin3 |
θdθ ∫cos2 |
ϕdϕ ∫ρ 4 = |
|
||||||||||||
G |
|
G′ |
|
|
|
|
|
|
|
0 |
|
0 |
0 |
|
|
|
|
R5 π |
|
|
1 |
|
|
2π |
πR5 π |
(cos2θ −1)d(cosθ )= |
4πR5 |
|
|||||
|
|
|
|
|||||||||||||
= |
|
∫sin3 |
θdθ ϕ |
+ |
|
sin 2ϕ |
|
= |
|
∫ |
|
. |
||||
5 2 |
2 |
5 |
15 |
|||||||||||||
|
0 |
|
|
|
|
0 |
0 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||||||
Задачі для самостійного розв’язування
5.1. Обчисліть ∫∫∫(x2 + y2 + z2 )dxdydz , якщо область G обмежена цилі-
G
ндром x2 + z2 =1 та площинами y = 0, y =1.
33

5.2. |
Обчисліть |
|
∫∫∫dxdydz, |
якщо |
область |
G обмежена |
параболоїдом |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
G |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
z ≥ |
x2 + y2 |
та сферою x2 + y2 + z2 ≤ 3a2. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
2a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
5.3. |
Обчисліть |
|
∫∫∫(x2 + y2)dxdydz, |
якщо область G обмежена поверхня- |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
G |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
ми z = |
x2 |
+ y2 |
|
та z = 2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
5.4. |
Обчисліть |
|
∫∫∫z |
|
|
|
x2 + y2dxdydz, якщо область G обмежена цилінд- |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
G |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
ром x2 + y2 = 2x та площинами y = 0, z = 0, z = a . |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
5.5. |
Обчисліть |
|
∫∫∫(x2 + y2)dxdydz, |
якщо область G обмежена поверхня- |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
G |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
ми z ≥ 0, r2 ≤ x2 + y2 + z2 ≤ R2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
1+ (x2 + y2 + z2) |
|
|
|
dxdydz , |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
5.6. |
Обчисліть |
|
∫∫∫ |
2 |
якщо |
область |
G |
|
|
куля |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
G |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
x2 + y2 + z2 ≤1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
5.7. |
Обчисліть |
|
∫∫∫xydxdydz , якщо |
область |
G обмежена |
поверхнями |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
G |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
x2 + y2 = 3, z = 0, z = 4, x ≥ 0, y ≥ 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
5.8. |
Обчисліть |
|
∫∫∫z |
|
|
|
x2 + y2dxdydz , |
якщо область G обмежена поверх- |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
G |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
нями z ≥ 0, z = 3 − x2 − y2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
5.9. |
Обчисліть |
|
∫∫∫ |
|
x2 + y2 + z2 dxdydz , |
якщо область |
G обмежена сфе- |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
G |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
рою x2 + y2 + z2 = z . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
5.10. Обчисліть |
|
∫∫∫ |
|
|
|
dxdydz |
|
|
|
|
, |
|
|
якщо |
|
область |
G |
– |
|
|
куля |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
G x2 + y |
2 + (z − 2) |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
x2 + y2 + z2 ≤ 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
5 |
|
π . |
5.2. πa3 |
|
|
|
|
+1). |
|
|
`16 |
π |
. 5.4. |
|
|
8a2 |
. |
|||||||||||||||||||
|
Відповіді: 5.1. |
|
(6 |
3 |
5.3. |
||||||||||||||||||||||||||||||||||
6 |
|
3 |
|
9 |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|||||||||||||||||||||||
5.5. |
4 |
π (R5 − r5) . 5.6. |
8 |
π (2 |
|
−1). 5.7. |
9 |
. 5.8. |
6 |
3 |
π . 5.9. |
|
|
|
2 |
π . |
|||||||||||||||||||||||
2 |
. 5.10. |
||||||||||||||||||||||||||||||||||||||
|
|
|
5 |
|
|
|
3 |
||||||||||||||||||||||||||||||||
15 |
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|||||||||
34
Розрахункові завдання
Задача 8. Обчисліть потрійні інтеграли, перейшовши до сферичних або циліндричних координат.
|
|
|
|
|
|
1. |
∫∫∫ |
x2 + y2dxdydz; G : x2 + z2 = y2, y =1. |
|||
|
G |
|
|
|
|
2. |
∫∫∫(x2 + y2 + z2)dxdydz; G : x2 + y2 = 4,z = 0, z = 3. |
||||
|
G |
|
|
|
|
|
|
|
|
|
|
3. |
∫∫∫z |
|
x2 + y2dxdydz; G : x2 + y2 = 2x, y = 0, z = 0, z = a. |
||
|
G |
|
|
|
|
4.∫∫∫(4 − x2 − y2)dxdydz; G :2z = x2 + y2,z = 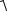
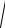 x2 + y2 , x ≥ 0, y ≥ 0.
x2 + y2 , x ≥ 0, y ≥ 0.
|
G |
|
||
5. |
∫∫∫xydxdydz; G : x2 + y2 =1, z = 0, z = 3, x ≥ 0, y ≥ 0 . |
|||
|
G |
|
||
|
|
|
|
|
6. |
∫∫∫x x2 + y2dxdydz; G : z = 4 − x2 − y |
2 , z = 0,x ≥ 0, y ≥ 0. |
||
|
G |
|
||
7. |
∫∫∫zdxdydz; G : x2 + y2 = 3,x2 + y2 + z |
2 = 4, z = 0 . |
||
|
G |
|
||
8. |
∫∫∫(x2 + y2)dxdydz; G : x2 + y2 = 4y,z = 0, z = 4. |
|||
G
9.∫∫∫(x2 + y2)dxdydz; G : z = 4 − x2 − y2,z = 0.
G
|
|
|
|
|
|
|
|
10. |
∫∫∫ |
x2 + y2dxdydz; G : x2 + y2 + z2 = 9, x2 + y2 = 8z . |
|||||
|
G |
|
|
|
|
||
11. |
∫∫∫ |
|
dxdydz |
|
; G : x2 + y2 + z2 = 4, x2 + y2 ≤1. |
||
|
|
|
|
||||
9 − x2 − y2 |
|||||||
|
G |
|
|
||||
12. ∫∫∫x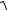
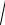 x2 + z2dxdydz; G : x = 4 − y2 − z2 , x = 0 .
x2 + z2dxdydz; G : x = 4 − y2 − z2 , x = 0 .
G
13. ∫∫∫ex2 + y2 dxdydz; G : x2 + y2 = z2z = 0, z = 3.
G
14. |
∫∫∫ |
|
|
xzdxdydz |
|
; G : x2 |
+ y2 |
= 2x,z =1, z = 2. |
||
|
|
|
|
|
||||||
x2 + y2 |
|
|||||||||
|
G |
|
|
|
|
|
||||
15. |
∫∫∫ |
x2 + y2dxdydz; G : z = x2 + y2, z = 4 . |
||||||||
|
G |
|
|
|
|
|
|
|||
16. ∫∫∫x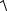
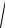 y2 + z2dxdydz; G : y2 + z2 = 9 , x = 0,x = 4.
y2 + z2dxdydz; G : y2 + z2 = 9 , x = 0,x = 4.
G
35

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
17. |
∫∫∫z |
|
x2 + e2dxdydz; G : z = 3 − y2 − x2 ,z ≥ 0. |
||||||||||||
|
G |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
18. |
∫∫∫xydxdydz; G : x2 + y2 = 3, z = 0, z = 4 . |
||||||||||||||
|
G |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
19. |
∫∫∫xyzdxdydz; G : x2 + y2 ≤ 4,x2 + y2 + z2 = 9. |
||||||||||||||
|
G |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
20. |
∫∫∫(z |
2 |
+ y |
2 |
) |
2 |
dxdydz; G : y = |
1 |
(x |
2 |
+ z |
2 |
), y = 2. |
||
|
|
|
|
|
2 |
|
|
||||||||
|
G |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
21. |
∫∫∫zdxdydz; G : z = x2 + y2, z = 0, z = 2. |
||||||||||||||
|
G |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
22. |
∫∫∫(z2 + y2)dxdydz; G : x2 + y2 = 9, z = 0, z = 4. |
||||||||||||||
|
G |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
23. |
∫∫∫(x2 + z2 )dxdydz, G : 2y = x2 + z2, |
y = 2. |
|||||||||||||
G
24. ∫∫∫
G
25. ∫∫∫
G
|
dxdydz |
|
; G : z = x |
2 |
+ y2,z = 4. |
|
||
|
|
|
|
|
||||
|
|
|
|
|
|
|||
|
4 − x2 − y2 |
|
|
|||||
|
|
|
|
|
|
|
||
ln(x2 + y2) |
dxdydz; G : x2 |
+ y2 = 4, y =1, |
y = 4. |
|||||
|
||||||||
|
x2 + z2 |
|
|
|
|
|
|
|
§6. ЗАСТОСУВАННЯ ПОТРІЙНОГО ІНТЕГРАЛА ДО ЗАДАЧ ГЕОМЕТРІЇ ТА МЕХАНІКИ
Основні теоретичні відомості
[1] – гл.VIII,§1, с.438-440; [2] – гл.10,§1, с.593-594; [3] – глава ХІV, §1-3, с.199-202; [4] – глава VII, §1, с.286-293; [5] – глава I, §1, с.23-28.
Об’єм області G знаходиться за формулою
V = ∫∫∫dxdydz .
G
Маса тіла із змінною густиною γ = γ (x, y,z) , що займає просторову область G , визначається за формулою:
|
m = ∫∫∫γ (x, y,z)dxdydz . |
|
G |
Статичні моменти тіла M xy,M yz ,M xz відносно координатних пло- |
|
щин Oxy, Oxz, Oyz : |
M xy = ∫∫∫zγ (x, y,z)dxdydz, |
G
M xz = ∫∫∫yγ (x, y,z)dxdydz ,
G
M yz = ∫∫∫xγ (x, y,z)dxdydz .
G
36
Координати центра мас тіла xc, yc,zc :
|
|
|
|
|
M yz |
|
|
|
|
∫∫∫xγ (x, y,z)dxdydz |
|
|
||
x |
c |
= |
|
|
= |
|
|
G |
, |
|||||
|
|
m |
|
∫∫∫γ (x, y,z)dxdydz |
||||||||||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
G |
|
|
|
|
|
|
|
|
M xz |
|
|
|
|
|
∫∫∫yγ (x, y,z)dxdydz |
|
|
|
y |
c |
= |
|
|
= |
|
G |
|
, |
|||||
m |
|
∫∫∫γ (x, y,z)dxdydz |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
G |
|
|
|
|
|
|
|
M xy |
|
|
|
|
∫∫∫zγ (x, y,z)dxdydz |
|
|
|||
z |
c |
= |
|
= |
G |
|
. |
|||||||
|
|
∫∫∫γ (x, y,z)dxdydz |
||||||||||||
|
|
|
|
m |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
||||
G
Моменти інерції тіла Ix, I y, Iz відносно координатних осей
Ox, Oy, Oz :
Ix = ∫∫∫(y2 + z2)γ (x, y,z)dxdydz ,
G
Iy = ∫∫∫(x2 + z2)γ (x, y,z)dxdydz ,
G
Iz = ∫∫∫(y2 + x2)γ (x, y,z)dxdydz .
G
Моменти інерції тіла Ixy, Ixz , I yz відносно координатних площин
Oxy, Oxz, Oyz :
Ixy = ∫∫∫z2γ (x, y, z)dxdydz,
G
Ixz = ∫∫∫y2γ (x, y,z)dxdydz ,
G
Iyz = ∫∫∫x2γ (x, y,z)dxdydz .
G
Момент інерції тіла Io відносно початку координат
Io = ∫∫∫(x2 + y2 + z2)γ (x, y,z)dxdydz .
G
Питання для самоконтролю
1.Наведіть формулу для знаходження об’єму тіла за допомогою потрійного інтеграла.
2.Наведіть формули для знаходження маси тіла, моментів інерції тіла, координат центра мас тіла.
37
|
|
|
|
|
|
|
|
|
Зразки розв’язування задач |
|
|
|
|
||||||||||||
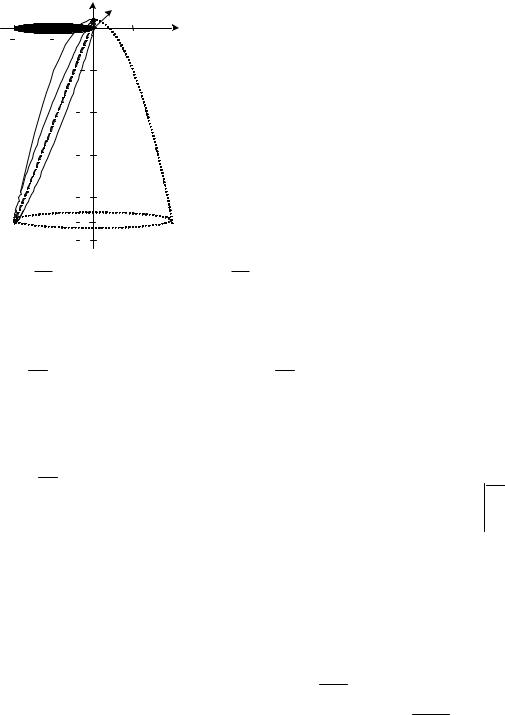
Приклад 1.Обчисліть |
об’єм |
тіла, |
обмеженого |
поверхнями |
|||||||||||||||||||||
z =1− 6(x2 + y2), z =12x +1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Розв’язання. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Визначимо проекцію заданого тіла на площину Oxy , для чого виклю- |
|||||||||||||||||||||||||
чимо z із системи |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
=1− |
6(x |
2 |
+ y |
2 |
), |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
z |
|
|
1− 6(x2 + y |
2) =12x +1 (x +1)2 + y2 =1. |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
=12x +1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
z |
y |
|
|
|
|
|
|
|
Отже, проекцією тіла (області G ) на площину |
|||||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
є круг, обмежений колом (x +1)2 + y2 =1. Пе- |
|||||||||||||||
2 |
1 |
|
0 |
|
1 |
|
x |
Oxy |
|||||||||||||||||
|
|
|
5 |
|
|
|
|
|
рейдемо до циліндричних координат. Тоді |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V = ∫∫∫ρdρdϕdz . |
|
|
|
|||||
G |
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
G ' |
|
|
|
|
|
|
|
|
|
|
15 |
|
|
|
|
|
|
|
|
Рівняння |
|
кола |
x2 + y2 = −2x , |
поверхні |
|||||||||
|
|
|
|
|
|
|
|
|
z =1− 6(x2 + y2) та площини z =12x +1 в циліндри- |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
20 |
|
|
|
|
|
чних |
координатах |
мають |
відповідно |
вигляд: |
||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
23 |
|
|
|
|
|
|
ρ = −2cosϕ, |
z =1− 6ρ 2, |
z =12ρ cosϕ +1, тому |
|||||||||||||
|
|
|
25 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3π |
|
|
|
|
|
|
|
|
|
|
3π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
−2cosϕ |
|
1−6ρ 2 |
|
2 |
|
−2cosϕ |
(1− 6ρ 2 −12ρ cosϕ −1)ρdρ = |
|
||||||||||||||
V = ∫ dϕ |
∫ρdρ |
|
|
∫dz |
= ∫ |
dϕ |
|
∫ |
|
|
|
||||||||||||||
π |
|
|
0 |
|
|
12ρ cosϕ +1 |
π |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
||||
2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3π |
|
|
|
|
|
|
|
|
|
|
|
|
3π |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
1+ cos2ϕ 2 |
dϕ = |
|
|
|
|
||||||
= ∫ (−24cos4 ϕ + 32cos4ϕ)dϕ =8 ∫ |
|
|
|
2 |
|
|
|
|
|
||||||||||||||||
π |
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
3π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3π |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ 2cos2ϕ + |
1+ cos4ϕ |
|
|
|
3 |
ϕ + sin2ϕ |
+ |
1 |
|
|
2 |
= 3π (куб.од). |
|||||||||||
= 2 ∫ |
1 |
|
|
|
2 |
|
dϕ =2 |
2 |
4 |
sin4ϕ |
π |
||||||||||||||
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Приклад 2. |
|
|
Знайдіть |
координати |
центра |
маси |
однорідного |
||||||||||||||||||
(γ (x, y,z) =1) тіла, яке обмежене площинами x = 0,z = 0, y =1, y = 3, x + 2z = 3. |
|||||||||||||||||||||||||
Розв’язання. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Знайдемо об’єм даного тіла: |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3−x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
3 |
|
|
2 |
3 |
3 |
3 − xdy = |
|
|
|
|||
|
|
|
|
|
V = ∫∫∫dxdydz = ∫dx∫dy |
|
∫dz = ∫dx∫ |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
G |
|
|
0 |
1 |
|
|
0 |
0 |
1 |
|
2 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
38 |
|
|
|
|
|
|
|
|
|
|
|
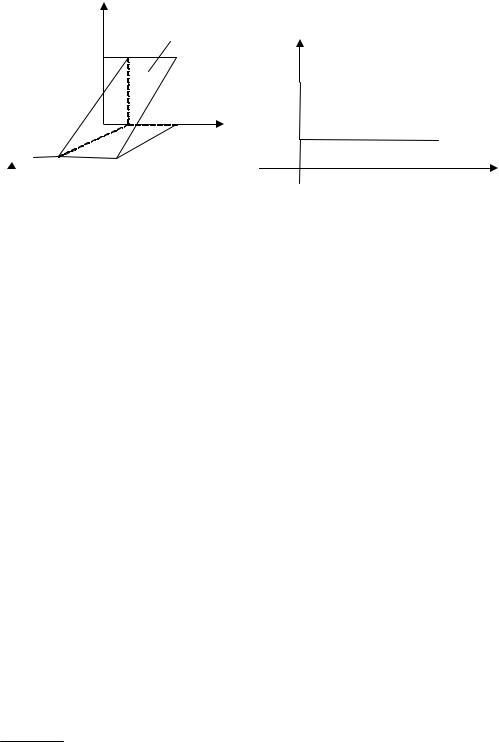
zx + 2z = 3
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
G |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
x |
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
2 |
|
|
3 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
= ∫(3 − x)dx |
= |
3x − |
|
|
|
|
x |
|
|
|
= |
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Тоді : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3−x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
3 |
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
3 − x dy = |
2 |
|
|
|
|
|
|
|
|
||||||||||||||
xc = |
∫∫∫xdxdydz = |
|
|
∫xdx∫dy |
|
∫dz = = |
∫xdx∫ |
∫x(3 − x)dx = |
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
9 |
G |
|
|
|
|
|
|
|
|
|
|
9 |
|
0 |
|
|
|
1 |
|
|
|
|
|
0 |
|
|
|
|
9 |
0 |
1 |
2 |
|
9 |
0 |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
2 |
|
3 |
|
|
|
|
1 |
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
= |
x |
2 |
− |
x |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
9 |
|
2 |
|
3 |
|
|
|
|
=1; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3−x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
3 |
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
||||||||||
yc = |
2 |
∫∫∫ydxdydz = |
|
2 |
∫dx∫ ydy ∫dz = 1 |
∫dx∫ y(3 − x)dy = |
|
|
∫(3 − x)dx = |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
9 |
G |
|
|
|
|
|
|
|
|
|
|
9 |
0 |
|
|
|
1 |
|
|
|
|
|
0 |
|
|
9 |
0 |
|
1 |
|
|
9 |
0 |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
4 |
|
|
|
x |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
= |
|
3x − |
|
|
|
|
|
|
= 2; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
9 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3−x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 3 3 |
|
|
|
|
|
|
|
|
|
|
3 (3 |
− x)2 3 |
|
|
|
|
|
|
|
− x)3 |
|
|
|
|||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
1 |
|
− (3 |
3 |
1 |
|
||||||||||||||||||||||||
zc = |
|
∫∫∫zdxdydz = |
|
|
|
|
∫dx∫dy |
∫zdz = |
|
∫ |
|
|
|
dx∫dy = |
|
|
|
|
|
|
|
|
|
|
|
= |
|
. |
||||||||||||||||||||||||
9 |
9 |
|
9 |
|
8 |
|
|
18 |
|
|
|
3 |
2 |
|||||||||||||||||||||||||||||||||||||||
|
G |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
1 |
|
|
|
|
|
0 |
|
|
|
0 |
|
|
1 |
|
|
|
|
|
|
0 |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Задачі для самостійного розв’язування
6.1. Знайдіть об’єм тіла, обмеженого даними поверхнями: а) z = 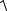
 x2 + y2 ,z = x2 + y2;
x2 + y2 ,z = x2 + y2;
б) 2z = x2 + y2,z = 2;
в) z = 0,2x = x2 + y2 , z2 + x2 + y2 = 4(всередині циліндра); г) y = x2 + z2, y =1;
д) x + y + z = 4, x = 2, y = 2, y = 0, x = 0, z = 0;; е) z2 + x2 + y2 = 2z , z2 = x2 + y2;
є) z = x2 + y2, z = x2 + 2y2, y = x, y = 2x, x = 1.
39
