3.3.4.3 Средний объем выборки

У однократных планов контроля необходимый объем выборки является величиной случайной только в случае контроля с прерыванием (см. табл.3.22). У двукратных планов эффективный объем выборки всегда является случайным. Рассмотрим сначала двукратный план контроля без прерываний. Количество изделий выборки, которые подлежат контролю, может принимать два значения:

если можно принять решение на основе первой выборки,

если необходимо взятие второй выборки. (3.131)

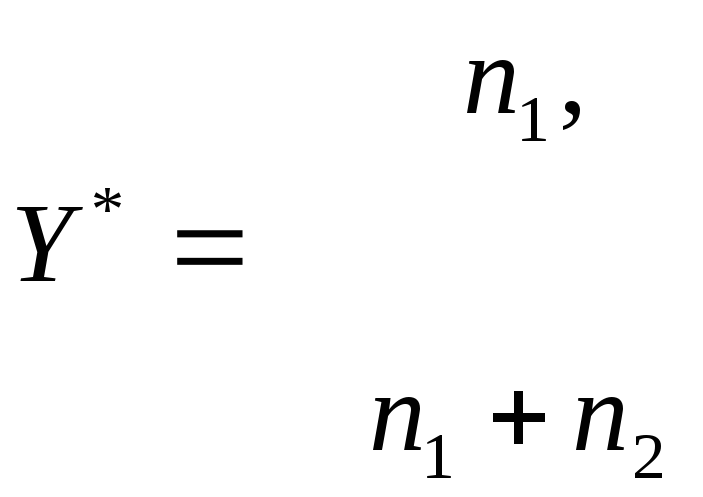
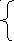
Математическое ожидание этой случайной величины обозначим аналогично (3.109) как средний объем выборки или (англ.: average sample number) для двукратного плана контроля

. (3.132)

Так как вероятности наступления обеих реализаций согласно (3.124) и (3.127) составляют:

,

,

то математическое ожидание (3.132) можно представить в виде

. (3.133)

Поскольку , то определенная на промежуткефункциядостигает наименьшего значенияв точкахи. Максимум кривойлежит и области. Соответствующее значение функцииявляетсямаксимальным значением или значением (анг.: average sample number limit) двукратного плана контроля без прерываний.

При контроле с прерыванием реализация необходимого объема выборкине превышает объема выборки при контроле без прерываний, то есть кривая для среднего объема выборкибудет более пологой. Для среднего объема выборки при контроле с прерываниемимеем

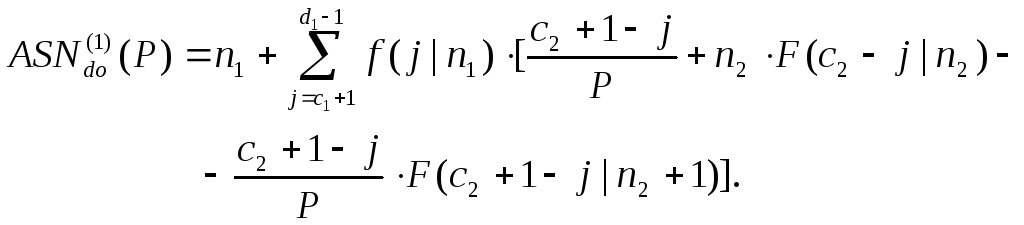(3.134)

При этом иобозначают вероят­ности обнаруженияили меньшедефектных изделий в выборке объемом.

Пример 3.58 Получим зависимость (3.133) и (3.134) для среднего объема выборки , исходя из представленного в примере 3.55 двукратного плана контроля при использовании биномиального распределения контрольной величины. Зависимость (3.133) дляв этом случае имеет следующий вид:

.

Некоторые значения этой функции можно очень просто вычислить, используя данные колонки 6 таблицы 3.28. Для вычисления последующих значений обратимся к формуле (3.124). Поскольку и, то

.

Для среднего объема выборки (3.134), используя формулы (3.110в) и (3.59а), получаем

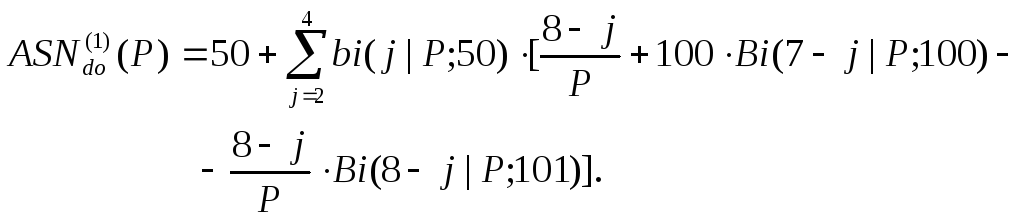
Графики полученных зависимостей представлены на рис. 3.35.

Пример 3.59 Вычислите, используя формулу (3.133), средний объем выборки для дву­кратного плана контроля из примера 3.57 при уровне дефектности . Исходное распределение является гипергеометрическим.

Согласно решению к примеру 3.133, в гипергеометрическом приближении .

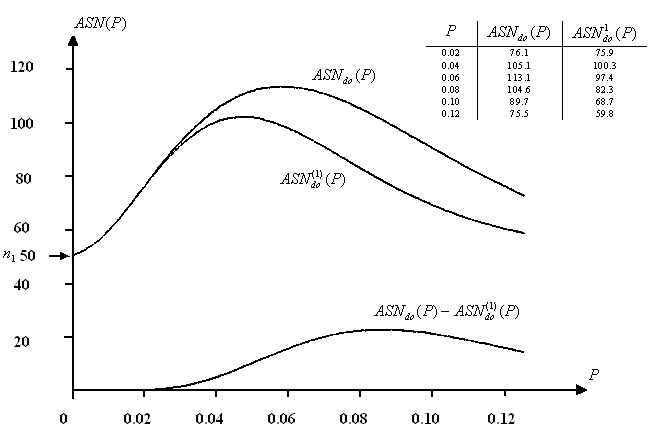
Рис.3.35 Зависимость для двукратного планапри контроле без прерываний и с прерываниями типа

Таким образом, получим

.

Пример 3.60 Вычислите для двукратного плана контроля из примера 3.56 с помощью формул (3.133) и (3.134) средний объем выборки при . Примените в этом случае распределение Пуассона.

Согласно решению к примеру 3.56, в приближении Пуассона , поэтому

.

При контроле с прерыванием типа это значение уменьшается: