3.3.2.2 Средний выходной уровень дефектности, предел среднего выходного уровня дефектности (и)

При работе с планом контроля () потребитель заинтересован не только в том, чтобы знать вероятность приемкипартии с засоренностью, но и число дефектных изделий, проходящих незамеченными через контроль. Применение данного плана () даже прини в коем случае не гарантирует, что будут приняты только годные изделия. Здесь можно гарантировать только то, что «хорошие» партии будут приниматься с большей вероятностью, «плохие» - с большей вероятностью будут браковаться.

В дальнейшем будем исходить из того, что производитель поставляет партии с постоянным уровнем дефектности . В партии объемомсодержится всегдадефектных изделий. Средняя доля дефектных изделий в принятых партиях называетсясредним выходным уровнем дефектности, сокращенно (англ.: average outgoing quality). Пусть обозначаетчисло дефектных изделий в принятой партии, a -число принятых изделий в этой партии. Переменные инужно рассматривать как условные математические ожидания. Запишемкак

. (3.96)

Средний выходной уровень дефектности является функцией уровня дефектностив поставляемых партиях, то есть. Эта функция для определенного уровня дефектностиимеет максимум. СоответствующеезначениеAOQ(P_М) называется пределом среднего выходного уровня дефектности, сокращенно AOQL (англ.: average outgoing quality limit)

. (3.97)

Сначала выясним, как при данном уровне дефектности определить по формуле (3.96) средний выходной уровень. Числопринятых изделий, математическое ожидание которого стоит в знаменателе выражения (3.96), определяется, во-первых, тем, как мы после контроля поступим с изделиями,входившими в выборку. Возможны три решения:

- - все изделия выборки (не только дефектные) после контроля отбраковываются без замены;

- - отбраковывают без замены только дефектные изделия;

- - отбраковывают только дефектные изделия, заменяя их при этом на годные (объем выборкиостается прежним).

Во-вторых, величина зависит от того, что происходит сизделиями остатка партии в случае ее забраковки. Возможны три варианта:

- - всеизделий остатка партии отбраковываются;

- - остаток партии подвергают сплошному контролю, при этом все дефектные изделия отбраковывают без замены на годные;

- - остаток партии подвергают сплошному контролю, а все дефектные изде­лия отсортировывают и заменяют на годные (объем остаткаостает­ся прежним).

В принципе, каждый из вариантов иможет выступать в комбинации с любым из вариантови. В случаях, когда в забракованных партиях производят сплошной контроль с заменой дефектных изделий годными, говорят обочищающем контроле (англ.: rectifying inspection). Очищающий контроль является комбинацией.

Различают в общей сложности девять комбинаций . Это нашло свое отражение в табл.3.15.

Для понимания приведенных в табл.3.15 зависимостей по определению среднего выходного уровня дефектности следует помнить, что математическое ожидание в числителе выражения (3.96) во всех девяти случаях одинаково. Убедимся, что все прошедшие через контроль дефектные изделия могут быть изделиями только из остатка партии, а не из самой выборки, так как или всеизделий выборки отсортировываются (), или удаляются только дефектные изделия (), или они заменяются годными ().

Количество дефектных изделий в остатке партии является случайной величиной . Ее математическое ожидание в принятых и забракованных партиях различно. В забракованных партиях, то есть при, проводится сплошной контроль с отбраковкой () или заменой () дефектных изделий, либо остаток партии отсортировывают полностью, не подвергая контролю (). Таким образом, гаран­тируется, что из остатка забракованной партии потребителю не попадет ни одного дефектного изделия

.

Если партия принимается, то есть в случае ,элементов остатка не контролируются и выполняется соотношение

.

Таким образом, для среднего числа прошедших через контроль дефектных изделий можно записать:

Таблица 3.15 Зависимости AOQ(P) для комбинаций принятия решения при однократных планах контроля

	Остаток партии больше не используется	Остаток после отбора дефектных изделий используется дальше	Остаток после замены дефектных изделий используется дальше
Выборка больше не используется
Выборка после отбора дефектных изделий используется дальше
Выборка после замены дефектных изделий используется дальше

при .

при ,

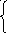
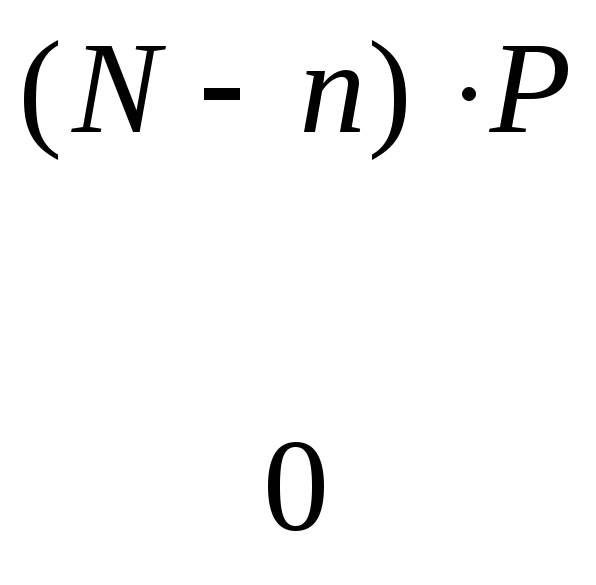(3.98)

Вероятности, с которыми выполняются условия или, являются вероятностями забраковкиили приемки партии, так что для искомого математического ожиданияотсюда следует:

.

В результате подстановки (3.98) получаем

. (3.99)

Средний выходной уровень дефектности во всех девяти случаях определяется одинаково (см. табл.3.15):

. (3.100)

М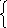атематическое ожидание числапринятых изделий из партии зависит от выбора комбинаций действий с выборкой и остатком партии. В качестве примера рассмотрим комбинацию. Переменную- как и переменную, можно представить как условное математическое ожидание. При условии, что партия припринимается, число, так как в этом случае объем партииуменьшается только на среднее число содержащихся в выборке дефектных изделий, которые, согласно, отбраковываются без замены. При условии, что партия призабраковывается, из партии, согласно, сначала будут удалены в среднемдефектных изделий, а затем, согласно, из проверяемого остатка партии удаляется в среднем ещедефектных изделий, так что. Таким образом

при

при (3.101)

Вероятности событий иравны соответственнои. Дляимеем

(3.102)

Путем подстановки (3.102) в (3.100) получается приведенная в табл.3.15 для комбинации формула для определения среднего выходного уровня де­фектности. Аналогично получаются формулы для вычисленияи в других случаях.

Из девяти комбинаций, приведенных в табл.3.15, на практике распространены лишь те, при которых решения по отношению к выборке и остатку партии одинаковы. Эти комбинации сстоят на главной диагонали.

Комбинации встречаются при разрушающем контроле. Равенство означает, что входной и выходной уровни дефектности совпадают, если поставляются партии с постоянной долей брака. Если оценку способа контроля производят на основании того, насколько средний уровень дефектностилежит ниже входного уровня, то разрушающий контроль дает наихудшие результаты. Разрушающий контроль имеет смысл тогда, когда поставляются партии с переменным уровнем качества. В этом случае он защищает потребителя от приемки «плохих» партий.

Комбинация типична для входного контроля товара потребителем, такт как он обычно не в состоянии заменить дефектные изделия на годные ни в выборке, ни в остатке партии. Потребитель может провести только выбраковку дефектных изделий.

Комбинация типична для внутрипроизводственного приемочного контроля производителем (контроль между двумя этапами изготовления или выходной контроль), так как производитель может заменить в выборке и в остатке партии дефектные изделия годными.

Остановимся на определении предела среднего выходного уровня дефектности . В случае имеет место , то есть определенный в интер­валесредний выходной уровень дефектностибудет наибольшим при; тогда. В других случаях, приведенных в табл.3.15, максимальное значение среднего выходного уровня дефектностиполучается из условия

, (3.103)

если предположить, что дифференцируема. Поясним определениеиз уравнения (3.103) на примере комбинацийи . В этих случаях особенно просто вычислить , так как функцииимеют здесь простой вид (определение предела среднего выходного уровня дефектности в других случаях будет рассмотрено ниже).

Применяя план контроля при комбинации решенийили , по табл.5.10 определяем, что , и, соответственно,. Значениеполучаем согласно (3.103) из условия

. (3.104)

Вычисление по нелинейному уравнению (3.104) возможно только численными методами. Результат, конечно, зависит от того, какую функциюберут за основу: гипергеометрическую (3.58), биномиальную (3.59) или же оперативной харак­теристики Пуассона (3.68). Для последнего случая существуют соотношения (см. табл.3.16) для различных приемочных чисел, в которые внесены вспомогательные параметрыи, с помощью которых можно вычислить интересующие значенияипри заданныхи, используя соотношения

(3.105а)

. (3.105б)

Таблица 3.16 Вспомогательные параметры для определения и соответствующего уровня дефектностипри одноступенчатом плане контроля

0	1.00	0.368	11	8.82	7.233	21	16.73	14.66	31	24.95	22.50
1	1.62	0.840	12	9.59	7.948	22	17.54	15.43	32	25.78	23.30
2	2.27	1.371	13	10.37	8.670	23	18.35	16.20	33	26.62	24.10
3	2.95	1.942	14	11.15	9.398	24	19.17	16.98	34	27.45	24.90
4	3.64	2.544	15	11.93	10.13	25	19.99	17.76	35	28.29	25.71
5	4.35	3.168	16	12.72	10.88	26	20.81	18.54	36	29.13	26.52
6	5.07	3.812	17	13.52	11.62	27	21..63	19.33	37	29.97	27.33
7	5.80	4.472	18	14.31	12.37	28	22.46	20.12	38	30.82	28.14
8	6.55	5.146	19	15.12	13.13	29	23.29	20.91	39	31.66	28.96
9	7.30	5.831	20	15.92	13.89	30	24.11	21.70	40	32.51	29.77
10	8.05	6.528

Пример 3.43 В табл.3.17 приведены значения девяти функций из табл.3.15 для плана контроля. При этом дляприменяется гипергеометрическая функция. Максимальное значениеобозначено звездочкой (^*).

Таблица 3.17 Характеристики плана контроляпри различных комбинациях решений относительно выборки и остатка партии

		при комбинациях
1	2	3	4	5	6	7	8	9	10	11
0	1	0	0	0	0	0	0	0	0	0
0.02	1	0.0200	0.0200	0.0200	0.0169	0.0169	0.0169	0.0168	0.0168	0.0169
0.04	1	0.0400	0.0400	0.0400	0.0338	0.0338	0.0338	0.0336	0.0336	0.0336
0.06	0.9971	0.0600	0.0598	0.0598	0.0509	0.0507	0.0503	0.0504	0.0503	0.0503
0.08	0.9895	0.0800	0.0792	0.0792	0.0680	0.0674	0.0674	0.0671	0.0665	0.0665
0.10	0.9758	0.1000	0.0978	0.0976	0.0851	0.0835	0.0833	0.0834	0.0821	0.0820
0.12	0.9556	0.1200	0.1153	0.1147	0.1021	0.0987	0.0982	0.1006	0.0968	0.0963
0.14	0.9287	0.1400	0.1313	0.1300	0.1190	0.1127	0.1117	0.1162	0.1101	0.1092
0.16	0.8954	0.1600	0.1457	0.1433	0.1357	0.1253	0.1235	0.1319	0.1221	0.1203
0.18	0.8563	0.1800	0.1582	0.1541	0.1522	0.1363	0.1333	0.1472	0.1323	0.1295
0.20	0.8122	0.2000	0.1688	0.1624	0.1624	0.1457	0.1410	0.1620	0.1409	0.1364
0.22	0.7640	0.2200	0.1773	0.1681	0.1842	0.1533	0.1463	0.1761	0.1476	0.1412
0.24	0.7125	0.2400	0.1837	0.1710	0.1995	0.1590	0.1494	0.1894	0.1525	0.1436
0.26	0.6590	0.2600	0.1880	0.1713*	0.2142	0.1628	0.1501*	0.2017	0.1555	0.1439*
0.28	0.6040	0.2800	0.1902	0.1691	0.2282	0.1648	0.1487	0.2129	0.1567*	0.1421
0.30	0.5492	0.3000	0.1905*	0.1648	0.2414	0.1651*	0.1454	0.2227	0.1561	0.1384
0.32	0.4947	0.3200	0.1888	0.1583	0.2536	0.1636	0.1402	0.2310	0.1539	0.1330
0.34	0.4417	0.3400	0.1854	0.1502	0.2647	0.1605	0.1334	0.2376	0.1508	0.1261
0.36	0.3907	0.3600	0.1802	0.1407	0.2744	0.1558	0.1254	0.2420	0.1448	0.1181
0.38	0.3423	0.3800	0.1734	0.1301	0.2825	0.1498	0.1163	0.2441*	0.1383	0.1093
0.40	0.2969	0.4000	0.1652	0.1188	0.2888	0.1426	0.1066	0.2437	0.1306	0.0998
0.42	0.2548	0.4200	0.1558	0.1070	0.2930	0.1342	0.0964	0.2403	0.1220	0.0898
0.44	0.2164	0.4400	0.1453	0.0952	0.2947*	0.1250	0.0860	0.2340	0.1126	0.0800
0.46	0.1817	0.4600	0.1340	0.0836	0.2937	0.1151	0.0758	0.2246	0.1027	0.0702
0.48	0.1507	0.4800	0.1221	0.0723	0.2896	0.1046	0.0658	0.2120	0.0924	0.0608

Анализ данных табл.3.17 позволяет сделать следующие выводы.

• В хороших партиях (при малых 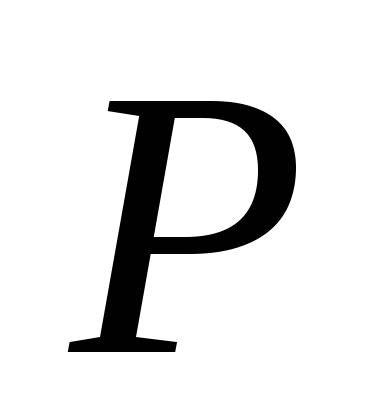) средний выходной уровень дефектности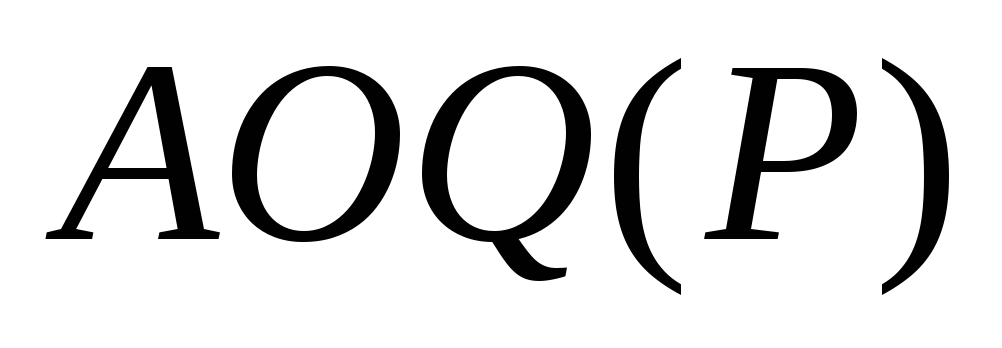также мал, как и входной уровень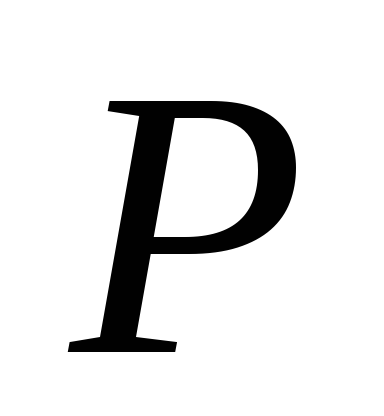, так как хорошие партии практически всегда принимаются. Последнее видно из второй колонки, где представлена вероятность приемки.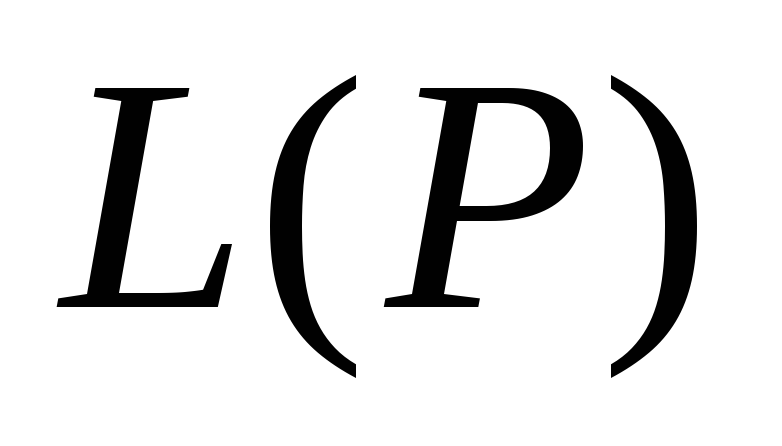

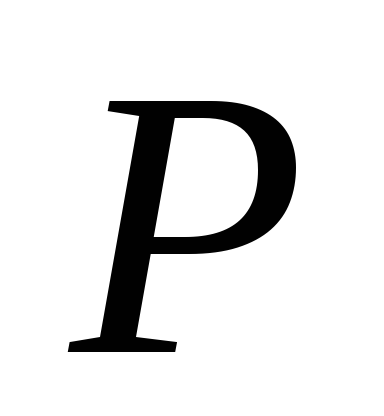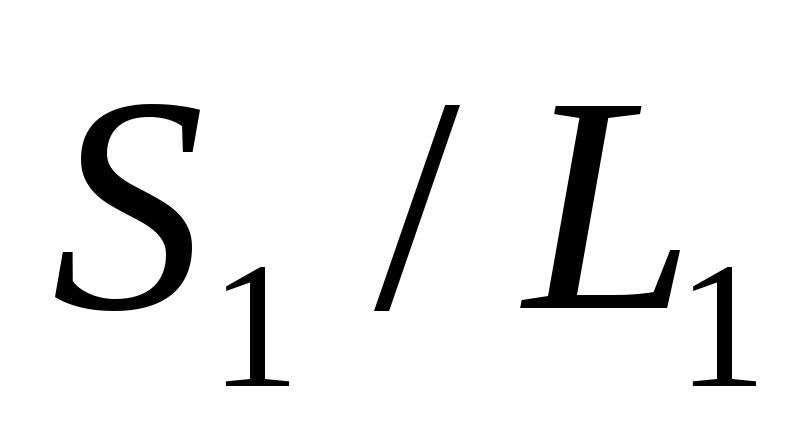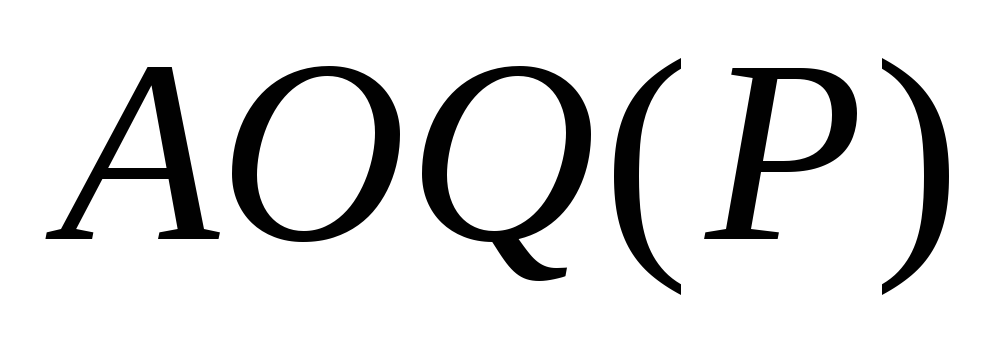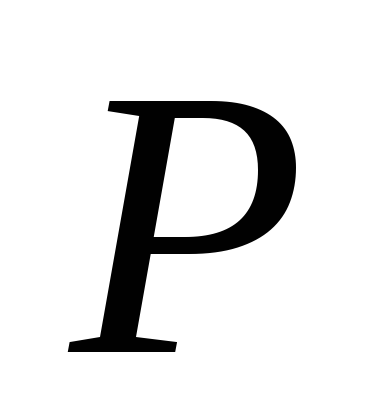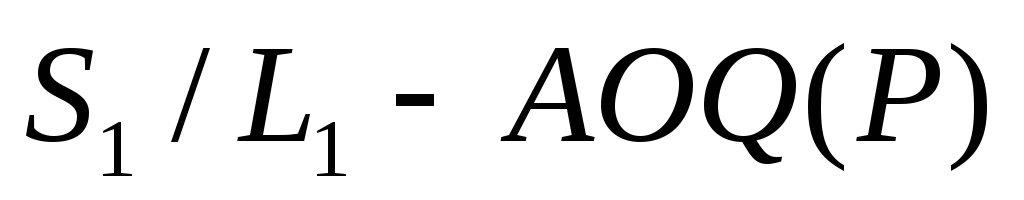• В плохих партиях (при больших ), если не принимать по внимание комбинацию ,средний выходной уровень дефектности низок. Он в любом случае значительно ниже входного уровня дефектности. Здесь контроль «фильтрует» сильнее. В данном случае, исключая комбинацию, при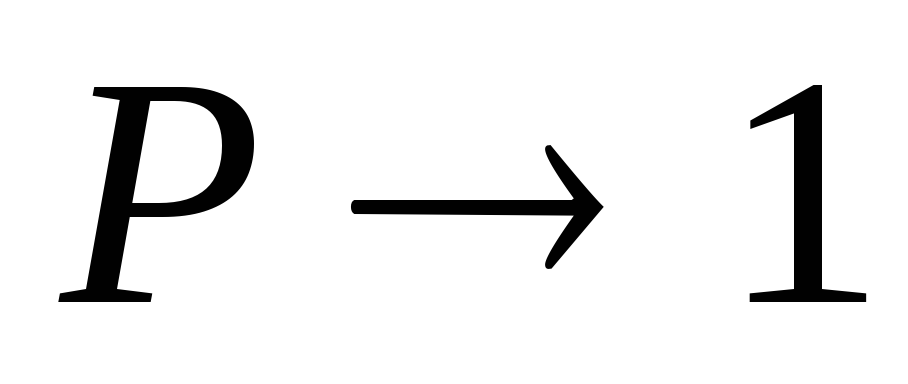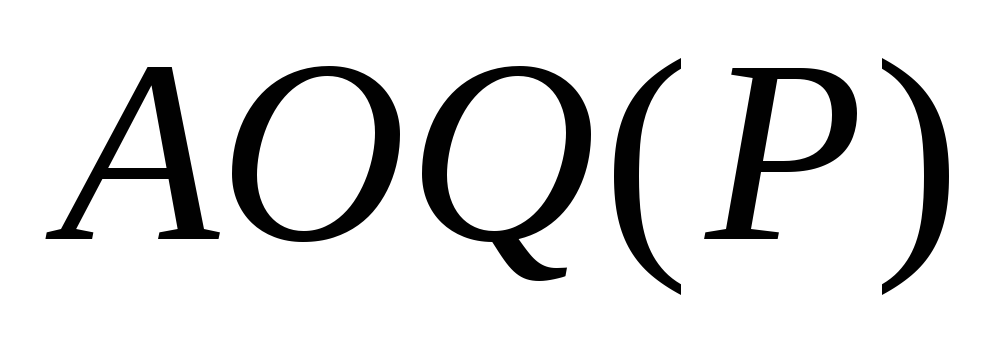стремится к нулю. Очевидно, что при большой доле брака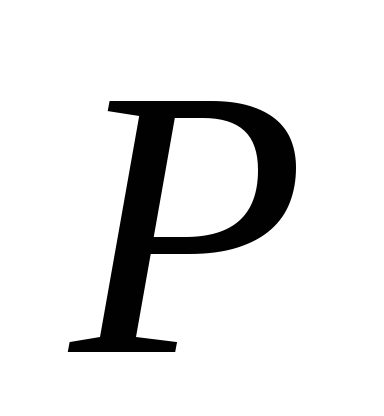остатки партии не будут приниматься без контроля.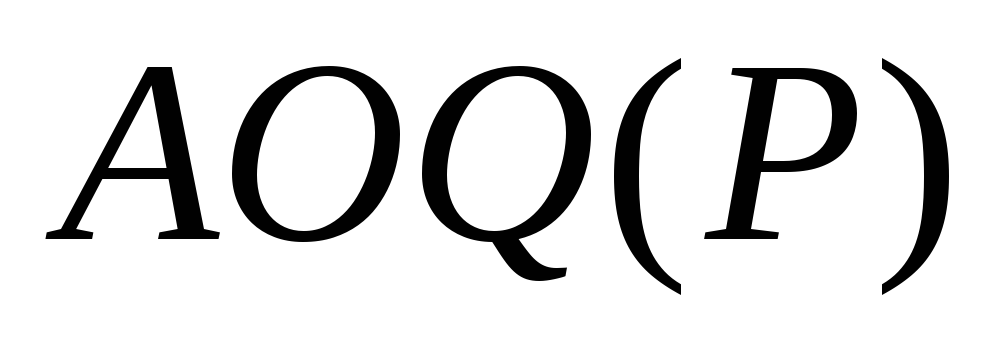

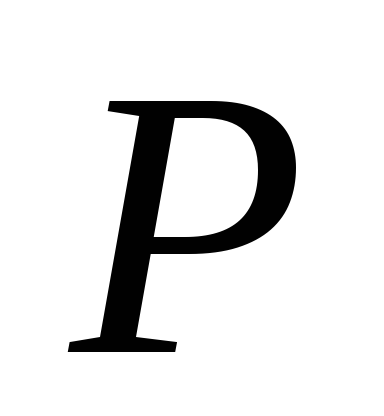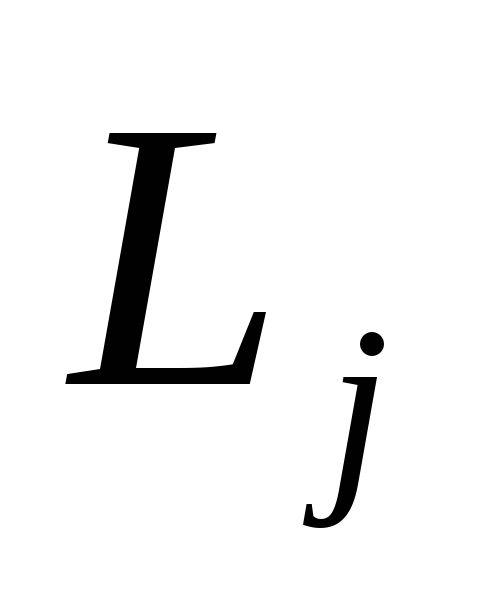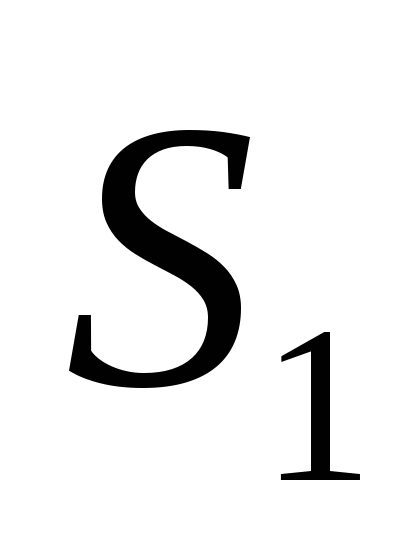• при любом уровне дефектности и любом принятом решенииотносительно остатка партии будет больше при решении, чем при решени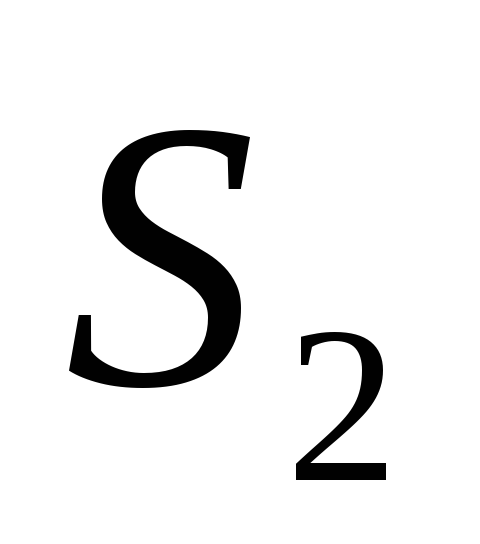и, а при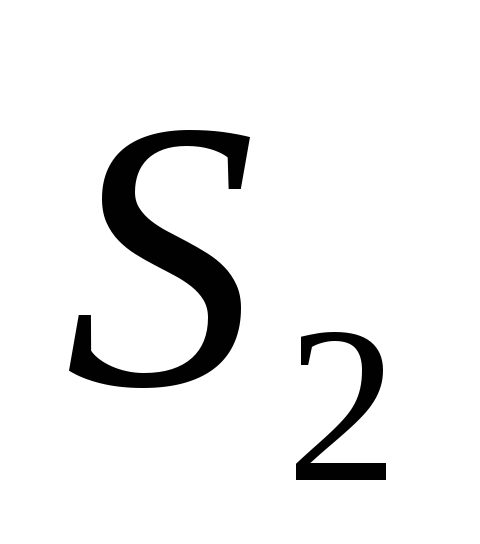больше, чем при. Соответственно ведут себя значения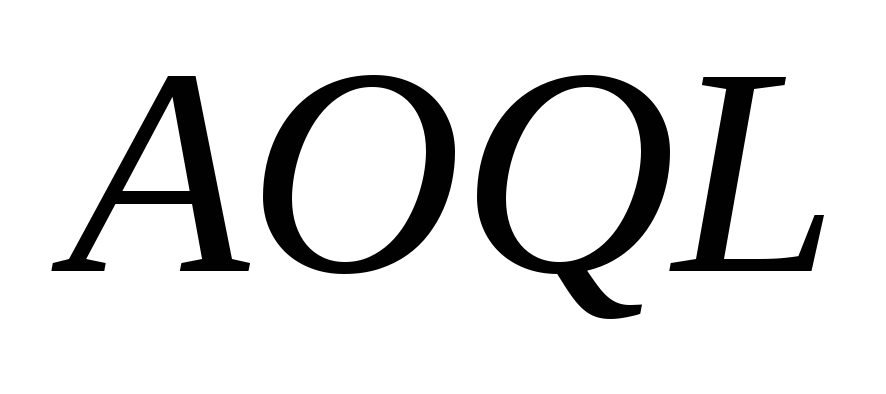при фиксированном решении.

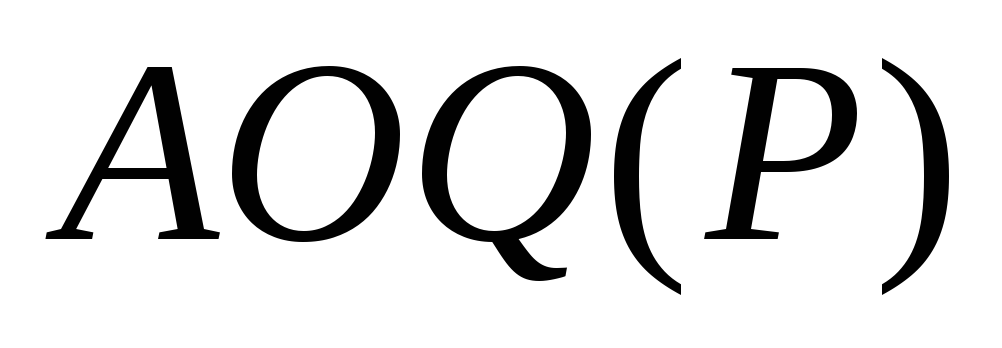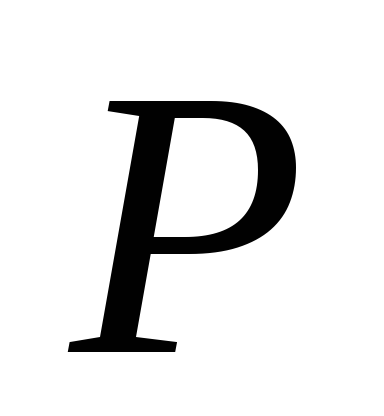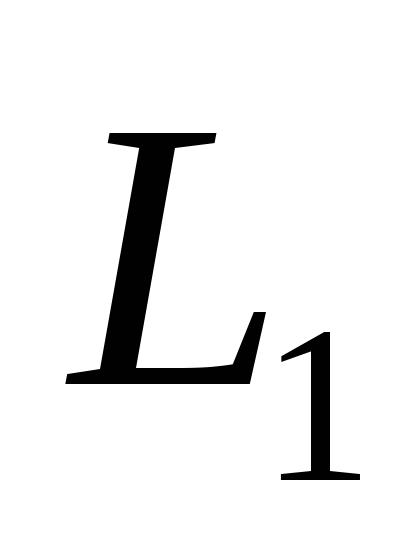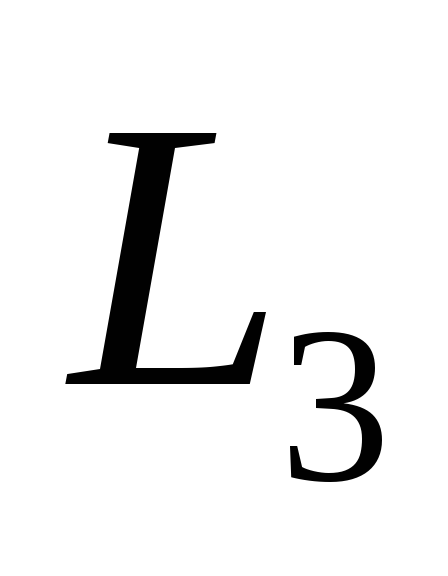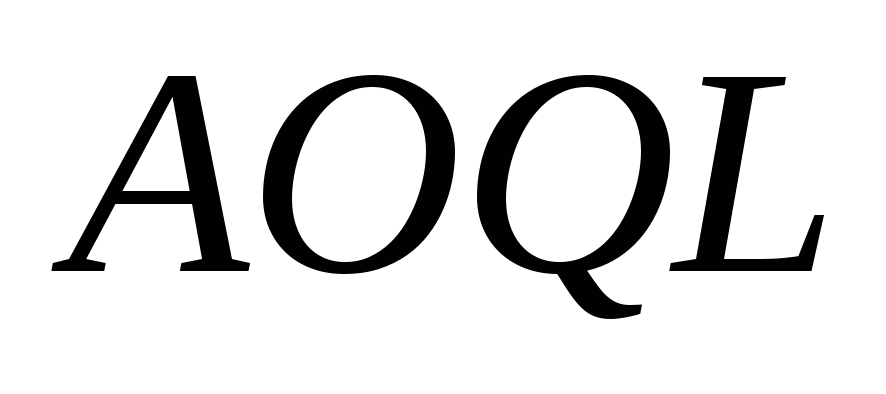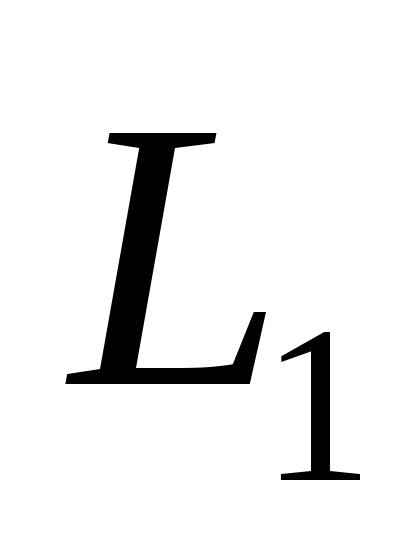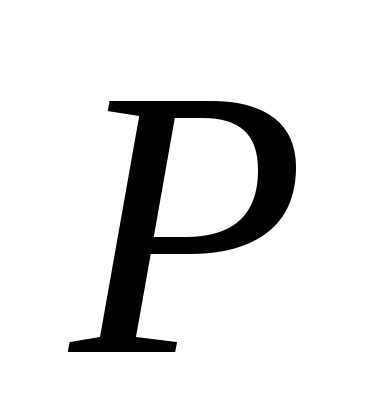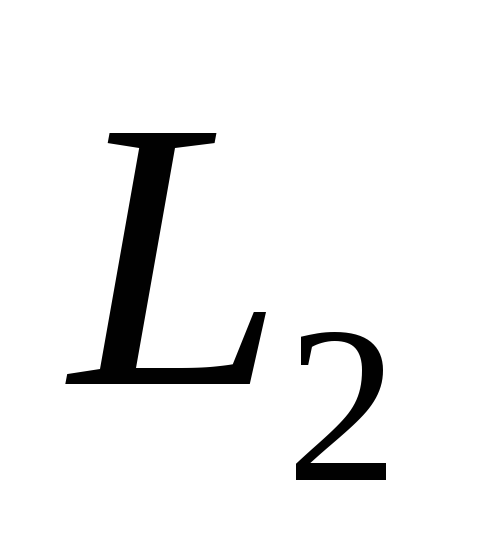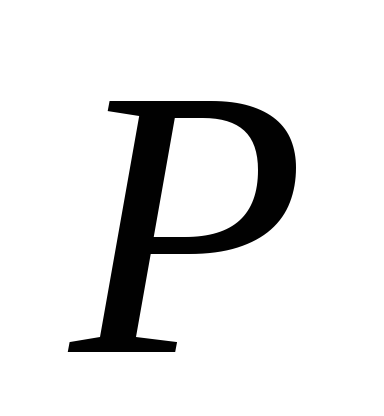• при любом уровне дефектности при данномимеет наибольшее значение при решении(остаток партии бракуется и не используется), а при решении(сплошной контроль остатка партии с заменой дефектных изделий годными) - наименьшее. Также ведут себя значения. При решениизначениедостигается при больших, чем при решении, и при тем больших, чем при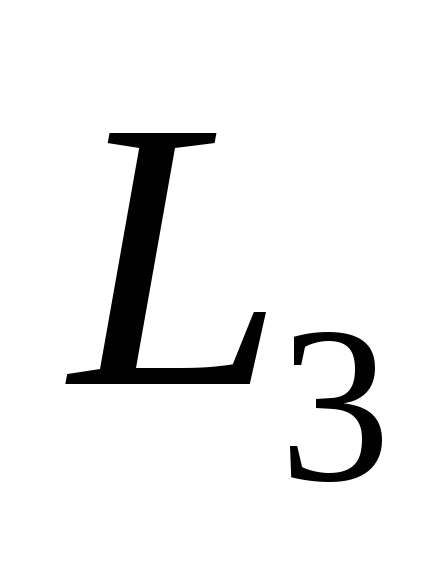. Эти результаты хорошо видны на гра­фиках (рис.3.25) функций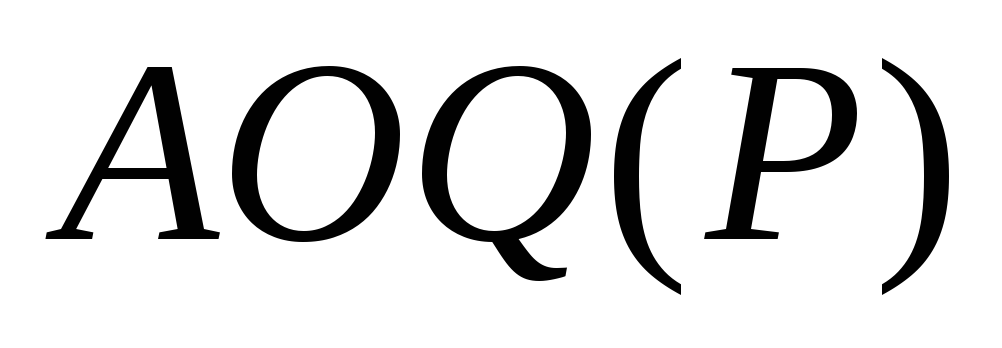для трех случаев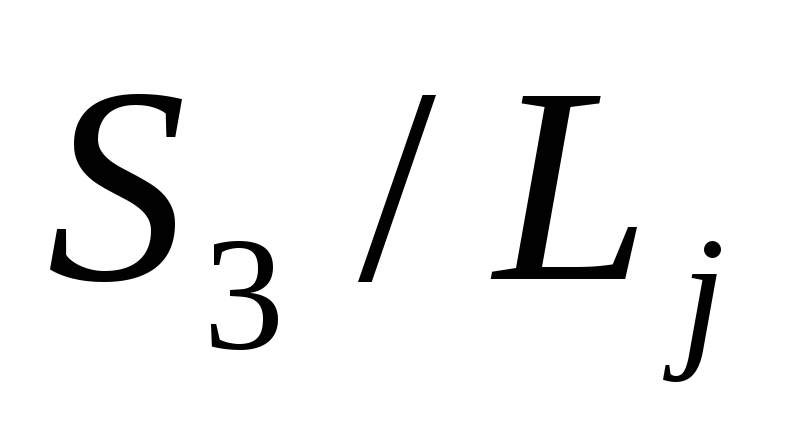. (см. колонки 9-11 в табл.3.17).

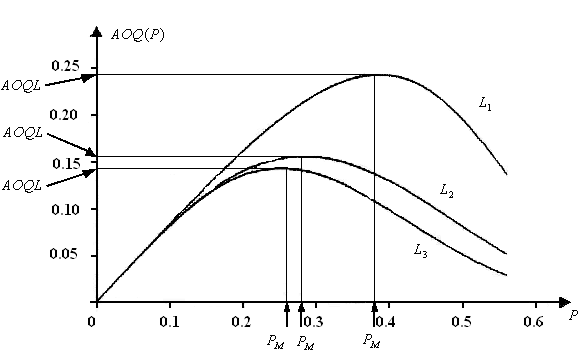
Рис.3.25 Кривые плана контроляпри различных решениях относительно остатка партии

С помощью табл.3.17 можно получить представление о качестве приближения формулами (3.105). По таблице, например, видно, что значение реализуется в случаев точкеи составляет

.

При применении формул (3.105) и табл.3.16 имеем и

.

Полное совпадение точного значения и значения, полученного с помощью (3.105), удивительно, если принять во внимание, что формула (3.105) базируется на аппроксимации Пуассона (3.66), которая мало подходит для плана.

Примечание

1. Исходя из значения слова «average outgoing quality» более точным было бы определять не по формуле (200), а как математическое ожидание отношения числа прошедших через контроль дефектных изделий к числу принятых изделий в партиях. Это определение по сравнению с (3.96) имело бы значительный недостаток - в этом случаеаналитически можно было бы представить, только используя сложные математические расчеты.

2. В литературе по контролю качества встречаются, прежде всего, формулы: и. Они корректны и адекватны для комбинацийи. Во всех остальных случаях они только приблизительны, но тем точнее, чем меньше доля бракаи/или относительный объем выборки.

Пример 3.44 Составьте таблицу аналогичную табл.3.17 для плана контроля . Используйте при этом полученные ранее шестнадцать значений для оперативной характеристики.

Таблица 3.18 Средний выходной уровень дефектности для простого плана контроля при различных комбинациях решений

		при комбинациях
1	2	3	4	5	6	7	8	9	10	11
0	1	0	0	0	0	0	0	0	0	0
0.02	0.8400	0.0200	0.0169	0.0168	0.0164	0.0142	0.0142	0.0163	0.0142	0.0141
0.04	0.7029	0.0400	0.0285	0.0281	0.0317	0.0240	0.0238	0.0315	0.0239	0.0236
0.06	0.5857	0.0600	0.0360	0.0350	0.0460	0.0304	0.0298	0.0453	0.0301	0.0295
0.08	0.4860	0.0800	0.0405	0.0389	0.0588	0.0342	0.0331	0.0575	0.0338	0.0327
0.10	0.4015	0.1000	0.0427	0.0402*	0.0701	0.0361	0.0343*	0.0678	0.0355	0.0337*
0.12	0.3301	0.1200	0.0431*	0.0396	0.0796	0.0364*	0.0339	0.0761	0.0357*	0.0333
0.14	0.2701	0.1400	0.0421	0.0378	0.0871	0.0356	0.0325	0.0821	0.0347	0.0318
0.16	0.2198	0.1600	0.0402	0.0352	0.0926	0.0340	0.0303	0.0857	0.0330	0.0295
0.18	0.1780	0.1800	0.0376	0.0320	0.0959	0.0318	0.0277	0.0870*	0.0307	0.0269
0.20	0.1432	0.2000	0.0348	0.0287	0.0971*	0.0293	0.0249	0.0860	0.0282	0.0241
0.22	0.1146	0.2200	0.0313	0.0252	0.0958	0.0264	0.0220	0.0826	0.0253	0.0212
0.24	0.0911	0.2400	0.0280	0.0219	0.0927	0.0236	0.0191	0.0776	0.0225	0.0184
0.26	0.0719	0.2600	0.0246	0.0187	0.0878	0.0208	0.0164	0.0712	0.0197	0.0157
0.28	0.0564	0.2800	0.0215	0.0158	0.0816	0.0181	0.0139	0.0640	0.0170	0.0133
0.30	0.0438	0.3000	0.0184	0.0131	0.0742	0.0155	0.0116	0.0561	0.0145	0.0110

Пример 3.45 Вычислите на основании предыдущей таблицы значение при комбинации решенийи сравните его с результатом, получающимся при применении приближенного решения (209).

Согласно табл.3.18 функция в случаеимеет максимум при, равный

.

По формуле (3.105) и данным табл.3.16 получаем

.

Пример 3.46 Сравните графики функций для планов контроляипри комбинации.

Зависимость для плановприидля комбинации решенийсогласно табл.3.15 определяется как

.

Кроме того, для всех имеет место неравенство [см. рис.3.18 – гипергеометрические оперативные характеристики для трех планов]

.

Поэтому график придолжен лежать выше, чем при, так как при более жестком контроле () незамеченным проходит меньшее число бракованных изделий. Используя данные табл.3.17 и 3.18 только в части комбинации, получаем кривые, изображенные на рис. 3.26.