2.1.1.4 Биномиальное распределение

Гипергеометрическое распределение было получено с помощью особенно наглядной модели. Из урны с черными ибелыми шарами отбиралисьшаров без возвращения. Вероятность при первой же попытке вытянуть черный шар составляла. При вытягивании второго элемента эта вероятность составляет, если первый вытянутый шар будет черным, и, если первый шар будет белым. Условная вероятность получения черного шара меняется в этой модели с каждым шагом.

Если же из описанной выше генеральной совокупности, распределенной по закону Бернулли, брать выборки с возвращением, то вероятность вытащить черный шар на каждом шаге постоянна и равна . При приемочном контроле по качественному признаку это значение соответствует доле брака в партии. Если черный шар снова интерпретировать как «успех», тогда общее число«успехов» в выборке подчиняетсябиномиальному распределению.

Биномиальное распределение c выглядит следующим образом:

в противном случае,

при ,

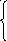
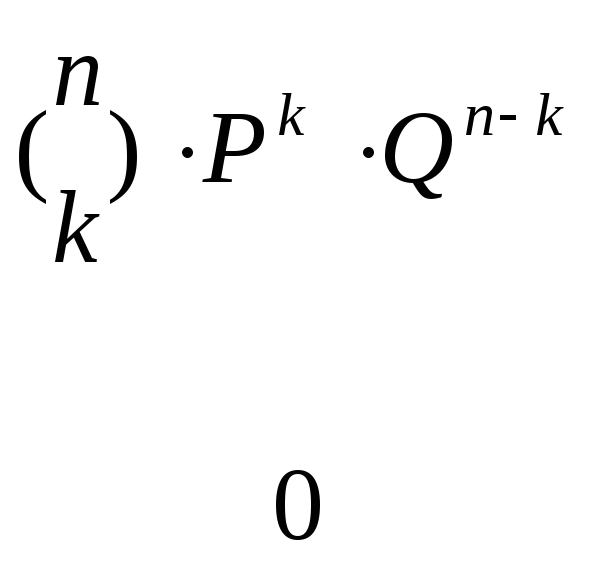(2.27)

а функция распределения определяется как:

при ,

при ,

при .

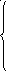
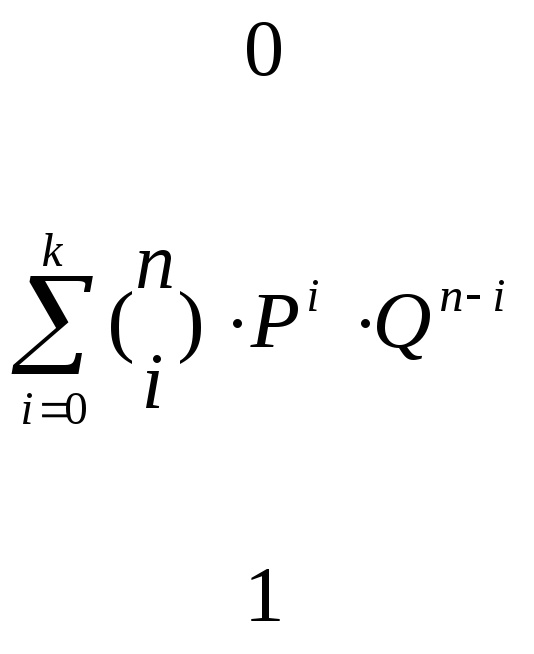(2.28)

На рис.2.4 изображены графики плотности биномиального распределения Бернулли и функции распределения при .

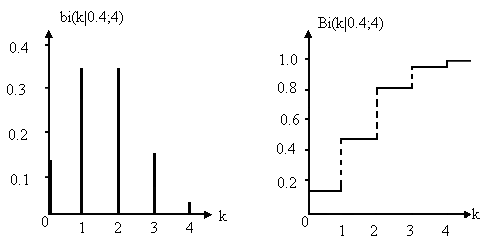
Рис.2.4. Графики плотности и функции распределения Бернулли при и.

Числовыми характеристиками -распределенной случайной переменнойявляются

, (2.29а)

. (2.29б)

При применении биномиального распределения очень удобными являются рекуррентные формулы:

; (2.30а)

(2.30б)

и отношения симметрии

, (2.31а)

. (2.31б)

Отношение симметрии (2.31а) говорит о том, что при вероятности успеха вероятность иметь«успехов» средиэлементов совпадает с вероятностью иметь«неудач» среди тех жеэлементов, еслиявляется вероятностью «неудач». Выражение (2.31б) показывает соотношение между вероятностями двух взаимодополняющих событий, а именносредиэлементов «успех» встречается максимумраз (левая часть выражения), и средиэлементов «неудача» встречается по крайней мерераз (правая часть).

Аналогом отрицательного гипергеометрического распределения является отрицательное биномиальное распределение, которое называют еще биномиальным распределением времени ожидания.

Пусть из урны с шарами, из которыхшаров черные, а оставшиесябелые, берут шары с возвращения до тех пор, пока не вытянут-ый черный шар. Проверяемой переменной в этой модели будет общее числотех шаров, которые следует вытянуть, чтобы встретился-ый черный шар, то естьэто случайный объем выборки. Отрицательное биномиальное распределение используют при анализе приемочного контроля с прерыванием (браковка партии согласно плану контроля при обнаружении-ого дефектного элемента в выборке из партии объемом).

Распределение вероятностей выглядит следующим образом:

в противном случае,

при ,

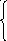
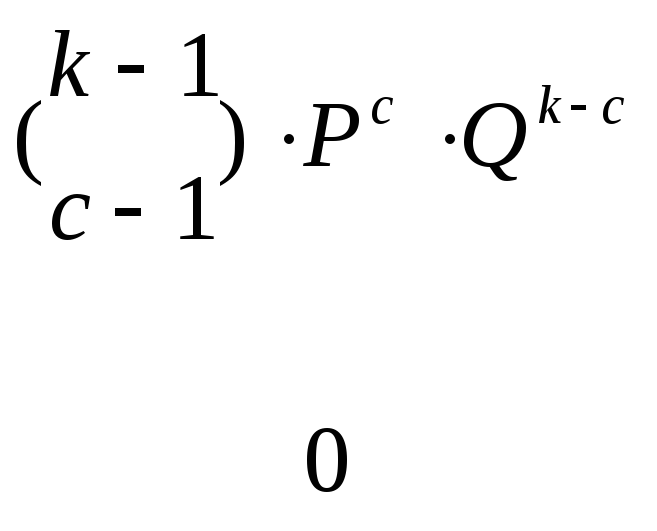(2.32а)

с параметрами и. В случаеотрицательное биномиальное распределение называется также геометрическим распределением, так как появляющиеся в (2.32а) вероятности составляют убывающую геометрическую последовательность.

Распределение (2.32а) можно записать и по-другому:

в противном случае,

при ,

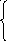
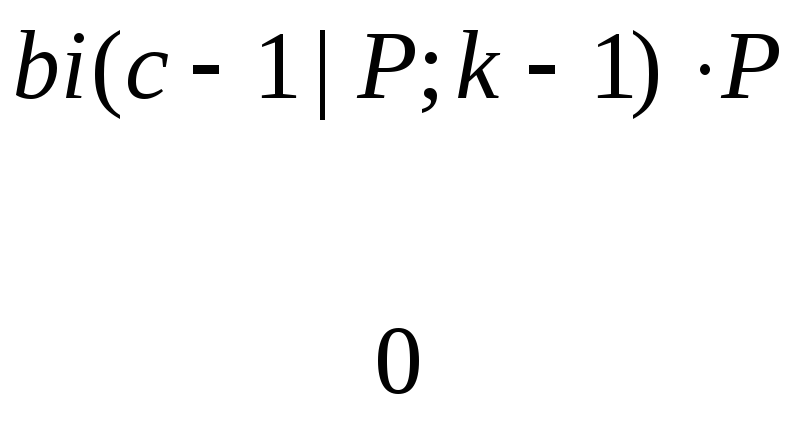(2.32б)

Функция отрицательного биномиального распределения в соответствии с (2.32а) имеет вид:

при .

при ,

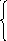
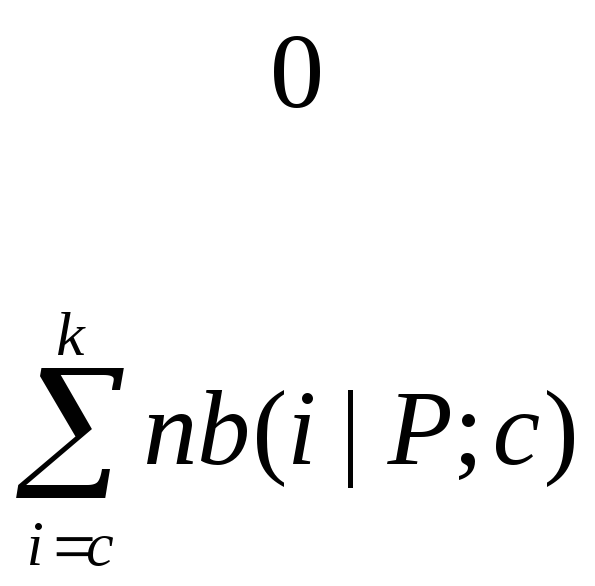(2.33а)

Числовые характеристики случайной величины , подчиняющейся отрицательному биномиальному распределению, определяются формулами:

, (2.34а)

. (2.34б)

Кроме того, имеют место рекуррентные соотношения:

, (2.35а)

. (2.35б)

Между биномиальным и гипергеометрическим распределениями имеется приближение

при условии, что ,и.

Пример 2.9. Вычислите и.

.

.

Пример 2.10. На предприятие поступает партия колпачков объемом , из которыхизделий дефектны. Из этой совокупности берут выборку с возвращением объемом. Вычислите вероятностивозможных значений. Вычислите также моду, математическое ожидание и дисперсию.

Случайная величина распределена по-ому распределению, где,, а. Тогда

,

,

,

,

,

.

Мода . Математическое ожидание, а дисперсия.

Пример 2.11. Из генеральной совокупности , в которой дефектных изделий, берутся колпачки с возвращением до тех пор, пока не обнаружат третий бракованный. Вычислите вероятность того, что объем данной выборки составитконденса­торов. Вычислите соответствующую вероятность дляи. Вычислите математическое ожидание и дисперсию?

Дискретная случайная величина распределена по . Тогда

,

,

,

,

.

Математическое ожидание и дисперсия соответственно:

, .