
Lineynaya algebra i analitich_geom / Ivleva_i_kurs_lekciy_po_lineynoy_algebre_i_analiticheskoy_ge
.pdfи коэффициентами характеристического уравнения dk для линейного оператора, действующего в трехмерном пространстве , при n = 3. Учитывая это, можно записать удобную формулу для нахождения характеристического уравнения линейного оператора, дейстующего в трехмерном пространстве:
( ) 3 I1 2 I2 I3
Лекция 14
Линейные операторы в евклидовом пространстве
Пусть линейный оператор А действует в евклидовом пространстве En и преобразует это пространство само в себя.
Введем определение: оператор А* назовем сопряженным оператору А, если для любых двух векторов x,y из Еn выполняется равенство скалярный произведений вида:
(Ax,y) = (x,A*y)
Еще определение: линейный оператор называется самосопряженным, если он равен своему сопряженному оператору, т. е. справедливо равенство:
(Ax,y) = (x,Ay)
или, в частности (Ax,x) = (x,Ax).
Самосопряженный оператор обладает некоторыми свойствами. Упомянем некоторые из них:
1.Собственные числа самосопряженного оператора - вещественны (без доказательства);
2.Собственные векторы самосопряженного оператора ортогональны. Действительно, если x1 и x2 – собственные векторы, а 1 и 2 – их собственные числа, то: Ax1 = 1x; Ax2 =
2x; (Ax1,x2) = (x1,Ax2), или 1(x1,x2) = 2(x1,x2). Поскольку 1 и 2 различны, то отсюда
(x1,x2) = 0, что и требовалось доказать.
3.В евклидовом пространстве существует ортонормированный базис из собственных векторов самосопряженного оператора А. Т. е. матрицу самосопряженного оператора
всегда можно привести к диагональному виду в некотором ортонормированном базисе,
составленном из собственных векторов самосопряженного оператора.
Еще одно определение: назовем самосопряженный оператор, действующий в евклидовом пространстве симметричным оператором. Рассмотрим матрицу симметричного оператора.
Докажем утверждение: чтобы оператор был симметричным, необходимо и достаточно, чтобы в ортонормированном базисе его матрица была бы симметричной.
Пусть А – симметричный оператор, т. е.: (Ax,y) = (x,Ay)
Если А – матрица оператора А, а x и y – некоторые векторы, то запишем:

|
|
x |
|
|
|
y |
|
|
||
|
|
|
1 |
|
|
|
|
1 |
|
|
X |
|
x2 |
|
Y |
|
y2 |
|
координаты x и y в некотором ортонормированном базисе |
||
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
xn |
|
|
|
yn |
|
|
||
Тогда: (x,y) = XTY = YTX и имеем (Ax,y) = (AX)TY = XTATY (x,Ay) = XT(AY) = XTAY,
т.е. XTATY = XTAY. При произвольных матрицах-столбцах X,Y это равенство возможно
Т
только при А = А, а это означает, что матрица А – симметричная.
Рассмотрим некоторые примеры линейных операторов
Оператор проектирования. Пусть требуется найти матрицу линейного оператора, осуществляющего проектирование трехмерного пространства на
координатную ось е1 |
в базисе е1, е2, е3. Матрица линейного оператора – это матрица, в столбцах |
|||||||||||
которой должны стоять образы базисных векторов |
е1 = (1,0,0), е2 = (0,1,0), е3 = (0,0,1). Эти образы, |
|||||||||||
очевидно, есть: |
|
|
Ае1 = (1,0,0) |
|
|
|
|
|
|
|
||
|
|
|
|
|
Ае2 = (0,0,0) |
|
|
|
|
|
|
|
|
|
|
|
|
Ае3 = (0,0,0) |
|
|
|
|
|
|
|
Следовательно, в базисе е1, е2, е3 |
матрица искомого линейного оператора будет иметь вид: |
|||||||||||
1 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
A 0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
Найдем ядро этого оператора. Согласно определению ядро – это множество векторов |
х, для |
|||||||||||
которых |
АХ = 0. Или |
|
|
|
|
|
|
|
|
|
||
|
1 |
0 0 |
x |
|
x 0 |
|
0 |
|
0 |
|
|
|
|
|
|
1 |
|
1 |
c1 |
|
|
|
|
|
|
|
0 |
0 0 * x2 |
0______ x2 |
X c1 1 c2 0 |
|
|
||||||
|
|
|
|
|
x3 |
c2 |
|
|
|
|
|
|
|
0 |
0 0 |
x |
|
|
0 |
|
1 |
|
|
||
Т. |
е. |
ядро оператора составляет множество векторов, |
лежащих в плоскости |
е1, |
е2. |
|||||||
Размерность ядра равна n – rangA = 2. |
|
|
|
|
|
|
|
|||||
Множество образов этого оператора – это, очевидно, множество векторов, коллинеарных |
е1. |
|||||||||||
Размерность пространства образов равна рангу линейного оператора и равна 1, что меньше размерности пространства прообразов. Т. е. оператор А – вырожденный. Матрица А тоже вырождена.
Еще пример: найти матрицу линейного оператора, осуществляющего в пространстве V3
(базис i, j, k) линейное преобразование – симметрию относительно начала координат.
Имеем: |
Ai = -i |
|
|
|
|
|
|
|
Aj = -j |
|
|
|
|
|
|
|
|
|
|
|
Ak = -k |
|
|
|
|
1 |
0 |
0 |
|
|
|
|
|
|
|
1 |
|
|
|
Т. е. искомая матрица |
A 0 |
0 |
|
|
|||
|
|
|
0 |
0 |
|
|
|
|
|
|
1 |
|
|
||
Рассмотрим линейное преобразование – симметрию относительно плоскости y = x. |
|||||||
|
|
|
Aj = i |
|
Ai = j |
(0,1,0) |
|
|
|
|
(1,0,0) |
|
|||
|
|
|
Ak = k |
(0,0,1) |
|
||
|
|
|
Матрица оператора будет: |
||||
|
|
|
|
0 |
1 |
0 |
|
|
|
|
|
|
0 |
|
|
|
|
|
A 1 |
0 |
|
||
|
|
|
|
|
0 |
|
|
|
|
|
|
0 |
1 |
|
|
|
|
|
|
Ai |
Aj Ak |
|
|
Еще пример – уже знакомая матрица, связывающая координаты вектора при повороте
осей координат. Назовем оператор, осуществляющий поворот осей координат, - оператор поворота.
Допустим, осуществляется поворот на угол :
Ai ’ = cos i + sin j
Aj ’ = -sin i + cos j
Матрица оператора поворота:
|
cos |
sin |
|
A |
|
|
|
|
cos |
|
|
|
sin |
|
|
|
Ai ‘ |
Aj ‘ |
|
Вспомним формулы преобразования координат точки при смене базиса – замена координат на плоскости при смене базиса:
x a cos x sin y
y b sin x cos y
Эти формулы можно рассматривать двояко. Ранее мы рассматривали эти формулы так, что
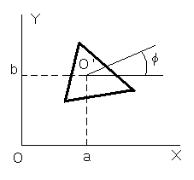
точка стоит на месте, поворачивается координатная система. Но можно рассматривать и так, что координатная система остается прежней, а перемещается точка из положения М* в положение М.
Координаты точки М и М* определены в той же координатной системе.
Все сказанное позволяет подойти к следующей задаче, которую приходится решать программистам, занимающимся графикой на ЭВМ. Пусть необходимо на экране ЭВМ осуществить поворот некоторой плоской фигуры (например треугольника) относительно точки О’ с
координатами (a,b) на некоторый угол . Поворот координат описывается формулами:
x* x* cos y* sin y* xsin ycos
Параллельный перенос обеспечивает соотношения:
x* x a
y* y b
Для того, чтобы решить такую задачу, обычно применяют искусственный прием: вводят так зазываемые “однородные” координаты точки на плоскости XOY:
(x, y, 1). Тогда матрица, осуществляющая параллельный перенос, может быть записана:
|
|
1 |
0 |
a |
|
|
|
|
|
1 |
|
|
|
|
T 0 |
b |
|
|||
|
|
|
0 |
1 |
|
|
|
|
0 |
|
|
||
Действительно: |
|
|
|
|
|
|
x* |
|
x |
|
x a |
||
|
|
|
|
|
|
|
y* T y y b |
||||||
|
|
|
|
|
1 |
|
1 |
|
1 |
|
|
|
|
А матрица поворота: |
|
|
|
|
|
|
|
cos |
sin |
0 |
|||
|
|
|
cos |
|
||
R sin |
0 |
|||||
|
|
0 |
|
0 |
|
|
|
|
|
|
1 |
||
Рассматриваемая задача может быть решена в три шага:
1й шаг: параллельный перенос на вектор А(-а, -b) для совмещения центра поворота с началом координат:
|
1 |
0 |
a |
||
T A |
|
|
1 |
|
|
0 |
b |
||||
|
|
0 |
0 |
1 |
|
|
|
|
|||
2й шаг: поворот на угол :
|
cos |
sin |
0 |
||
R |
|
|
cos |
|
|
sin |
0 |
||||
|
|
0 |
0 |
|
|
|
|
|
1 |
||
3й шаг: параллельный перенос на вектор А(а, |
b) |
для возвращения центра поворота в |
|||
прежнее положение: |
|
|
|
|
|
|
|
1 |
0 |
a |
|
|
|
|
1 |
|
|
|
TA 0 |
b |
|
||
|
|
|
0 |
|
|
|
|
0 |
1 |
|
|
Искомое линейное преобразование в матричном виде будет выглядеть:
x* |
|
|
|
|
x |
|
x |
|
|
|||
|
|
|
[T |
][R |
][T |
|
y |
|
|
y |
|
(**) |
y* |
] |
|
[D] |
|
||||||||
|
|
|
A |
|
|
A |
|
|
|
|
||
1 |
|
|
|
|
1 |
|
|
1 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|||
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos |
sin |
|
acos bsin a |
||||||
|
|
|
|
|
cos |
|
|
|
|
|
||
|
|
D sin |
|
1sin bcos b |
||||||||
|
|
|
|
0 |
|
0 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|||
По формуле (**) можно пересчитать координаты любой точки плоской фигуры, а затем построить ее на экране, осуществив тем самым ее поворот.
Лекция 15
Квадратичные формы и их приведение к каноническому виду
При рассмотрении евклидового пространства мы вводили определение квадратичной формы.
С помощью некоторой матрицы
|
a12 |
a13 |
|
a11 |
|
||
A a21 |
a22 |
a23 |
|
|
a32 |
a22 |
|
a31 |
|
||
строится многочлен второго порядка вида
n n
L(x1,x2, ,xn ) aijxixj
i 1 j 1
который называется квадратичной формой, порождаемой квадратной матрицей А.
Квадратичные формы тесно связаны с поверхностями второго порядка в n - мерном евклидовом пространстве. Общее уравнение таких поверхностей в нашем трехмерном евклидовом пространстве в декартовой системе координат имеет вид:
a11x2 a22 y2 a33z2 2a12xy 2a13xz 2a23yz a14x a24 y a34z a44 0
Верхняя строка - это не что иное, как квадратичная форма, если положить x1=x, x2=y, x3=z:
|
|
|
n n |
L(x1,x2,x3) aijxixj |
|||
|
|
|
i 1 j 1 |
|
a12 |
a13 |
|
a11 |
|
||
A a12 |
a22 |
a23 - симметричная матрица (aij = aji) |
|
|
a23 |
a22 |
|
a13 |
|
||
положим для общности, что многочлен
a14x a24 y a34z a44
есть линейная форма. Тогда общее уравнение поверхности есть сумма квадратичной формы,
линейной формы и некоторой постоянной.
Основной задачей теории квадратичных форм является приведение квадратичной формы к максимально простому виду с помощью невырожденного линейного преобразования переменных или, другими словами, замены базиса.
Вспомним, что при изучении поверхностей второго порядка мы приходили к выводу о том,
что путем поворота осей координат можно избавиться от слагаемых, содержащих произведение xy, xz, yz или xixj (i j). Далее, путем параллельного переноса осей координат можно избавиться от линейных слагаемых и в конечном итоге свести общее уравнение поверхности к виду:
P(x, y,z) a11x2 a22 y2 a33z2 c 0
В случае квадратичной формы приведение ее к виду
L(x,y,z) 1x2 2y2 3z2
называется приведением квадратичной формы к каноническому виду.
Поворот осей координат есть не что иное, как замена одного базиса другим, или, другими словами, линейное преобразование.
Запишем квадратичную форму в матричном виде. Для этого представим ее следующим образом:
L(x,y,z) = x(a11x+a12y+a13z)+ +y(a12x+a22y+a23z)+ +z(a13x+a23y+a33z)
|
x |
|
|
Введем матрицу - столбец |
y |
|
|
|
z |
Тогда L(x, y,z) X T AX |
- где X T =(x,y,z) |
- матричная форма записи квадратичной формы. Эта формула, очевидно, справедлива и в общем случае:
L(x1,x2 , ,xn ) X T AX
Канонический вид квадратичной формы означает, очевидно, что матрица А имеет диагональный вид:
|
|
|
1 |
0 |
|
|
|
|
|
|
|
|
0 x |
|
|||
L(x,y,z) (x,y,z) 0 |
2 |
|
0 y X'AX |
|||||
|
|
|
0 |
0 |
|
|
|
|
|
|
|
3 z |
|
||||
Рассмотрим некоторое линейное преобразование |
X = SY, где S - квадратная матрица |
|||||||
порядка n, а матрицы - столбцы Х и У есть: |
|
|
|
|
|
|
||
|
x |
|
|
|
|
y |
|
|
|
1 |
|
|
|
|
1 |
|
|
X |
x2 |
|
Y |
y2 |
|
|||
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
xn |
|
|
yn |
|
|||
Матрица S называется матрицей линейного преобразования. Отметим попутно, что всякой матрице n-ного порядка при заданном базисе соответствует некоторый линейный оператор.
Линейное преобразование X = SY заменяет переменные x1, x2, x3 новыми переменными y1, y2, y3. Тогда:
L(x, y,z) X T AX YT ST AXY YT BY где B = S T A S
Задача приведения к каноническому виду сводится к отысканию такой матрицы перехода S,
чтобы матрица В приобрела диагональный вид:
(*)
Итак, квадратичная форма с матрицей А после линейного преобразования переменных переходит в квадратичную форму от новых переменных с матрицей В.
Обратимся к линейным операторам. Каждой матрице А при заданном базисе соответствует некоторый линейный оператор А. Этот оператор имеет, очевидно, некоторую систему собственных чисел и собственных векторов. Причем, отметим, что в евклидовом пространстве система собственных векторов будет ортогональна. Мы доказывали на предыдущей лекции, что в базисе собственных векторов матрица линейного оператора имеет диагональный вид. Формула (*), как мы помним, это формула преобразования матрицы линейного оператора при смене базиса. Положим,
что собственные вектора линейного оператора А с матрицей А - это вектора у1, y2, ..., yn.
~
Ay1 1y1
~
Ay2 2 y2
Т. е.
~
Ayn n yn
А это означает, что если собственные вектора у1, y2, ..., yn взять за базис, то матрица линейного оператора в этом базисе будет диагональной
|
|
1 |
0 |
|
0 |
|
|
2 |
|
|
|
B |
0 |
|
0 |
||
0 0 n
или В = S-1 А S, где S – матрица перехода от первоначального базиса {e} к базису {y}. Причем в ортонормированном базисе матрица S будет ортогональной.
Т. о. для приведения квадратичной формы к каноническому виду необходимо найти собственные числа и собственные векторы линейного оператора А, имеющего в первоначальном базисе матрицу А, которая порождает квадратичную форму, перейти к базису собственных векторов и в новой системе координат построить квадратичную форму.
Обратимся к конкретным примерам. Рассмотрим линии второго порядка.
|
|
i |
i |
|
|
|
|
|
|
2 |
|
|
|
|
||||
|
aij xi xj |
2 bi xi c 0 |
или a11x1 |
2 a22 x2 |
2 2a12 x1x2 2b1x1 2b2x2 c 0 |
|||||||||||||
|
|
i 1 |
j 1 |
|
|
|
|
|
|
i 1 |
|
|
|
|
||||
С помощью поворота осей координат и последующего |
параллельного переноса осей это уравнение |
|||||||||||||||||
можно привести к виду ( переменные и коэффициенты переобозначены х1 = х, х2 = у): |
||||||||||||||||||
1) |
x2 |
|
2 |
y2 c 0 |
если линия центральная, 1 |
0, |
2 0 |
|||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2) |
1y2 2x 0 |
|
если линия нецентральная, т. е. один из i = 0. |
|||||||||||||||
|
Напомним виды линий второго порядка. Центральные линии: |
|||||||||||||||||
1) |
|
x2 |
|
|
|
|
y |
2 |
|
|
1 |
|
эллипс; |
|
|
|
|
|
|
a2 |
|
|
|
b |
2 |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
2) |
|
x2 |
|
|
y2 |
|
|
1 |
|
гипербола; |
|
|
|
|
||||
|
a2 |
|
b |
2 |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
3) |
|
x2 |
|
y2 |
|
|
0 |
|
точка; |
|
|
|
|
|||||
|
a2 |
b |
2 |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
4) |
|
x2 |
|
|
|
y2 |
|
|
0 |
|
две пересекающиеся прямые. |
|
||||||
|
a2 |
|
|
2 |
|
|
|
|
||||||||||
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|||
Нецентральные линии: |
|
|
|
|
||||||||||||||
5) |
х2 = а2 |
|
|
|
|
|
две параллельные линии; |
|
|
|
||||||||
6) |
х2 = 0 |
|
|
|
|
|
две сливающиеся прямые; |
|
|
|
||||||||
7) |
у2 = 2рх |
|
|
|
парабола. |
|
|
|
|
|||||||||
Для нас представляют интерес случаи |
1), 2), 7). |
|
|
|
||||||||||||||
|
Рассмотрим конкретный пример. |
|
|
|
|
|||||||||||||
|
Привести к каноническому виду уравнение линии и построить ее: |
|||||||||||||||||

5х2 + 4ху + 8у2 - 32х - 56у + 80 = 0.
|
|
|
|
5 |
2 |
|
. Характеристическое уравнение: |
|
Матрица квадратичной формы есть A |
|
|
|
|||||
|
|
|
|
|
2 |
8 |
|
|
|
|
|
|
|
|
|
||
|
5 |
2 |
|
(5 )(8 ) 4 2 13 36 0 Его корни: |
||||
|
|
|||||||
|
2 |
8 |
|
|||||
|
|
|
|
|
|
|
||
|
|
|
|
13 |
|
|
|
169 |
36 |
13 |
|
5 |
|
|
|
|
|
|
|
|
|
|
4 |
|
|
9 |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
1,2 |
|
|
|
|
2 |
|
|
|
|
|
|
4 |
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
1 |
|
|
|
2 |
|
||||||||||
Найдем собственные векторы: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 i u1 2u2 0 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(8 i)u2 |
0 |
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2u1 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
При 1 |
u 2u |
|
|
0 |
|
|
|
|
|
u1 = -2u2; u1 = 2c, u2 = -c |
или g1 = c1(2i – j). |
|||||||||||||||||||||||||||||||||||
= 4: |
1 |
|
|
|
|
|
2 |
|
|
|
0 |
|
||||||||||||||||||||||||||||||||||
|
2u1 4u2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
При 2 |
4u1 2u2 0 |
|
2u1 = u2; |
u1 = c, u2 = 2c |
или |
g2 = c2(i+2j). |
||||||||||||||||||||||||||||||||||||||||
= 9: |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
2u1 u2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Нормируем эти векторы: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
g |
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
1 |
|
|
|
|||||||||||||
|
e |
|
|
|
|
|
|
|
|
|
|
|
(2c i c j) |
|
|
|
|
|
i |
|
|
|
|
|
|
|
j |
|
|
|
||||||||||||||||
|
|
g |
|
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
1 |
|
|
|
1 |
|
|
|
|
5 |
|
1 |
1 |
|
|
|
|
5 |
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
g |
2 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
2 |
|
|
|
|
|
||||||||||
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
(c |
i 2c |
|
j) |
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
j |
|
|
|
|||||||||
|
|
|
|
|
|
c2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
2 |
|
|
|
g2 |
|
|
|
|
|
5 |
2 |
|
|
2 |
|
|
|
5 |
|
|
|
|
|
|
5 |
|
|
|
|
|
|||||||||||||||
Составим матрицу линейного преобразования или матрицу перехода к базису g1, g2:
|
|
2 |
|
|
|
|
|
1 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
5 |
|
|
|
|
5 |
|
||||||||
T |
|
|
|
|
|
|
|
- ортогональная матрица ! |
|||||||
|
|
1 |
|
|
|
|
2 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
5 |
|
|
|||||||||||
|
|
5 |
|
|
|
|
|
||||||||
Формулы преобразования координат имеют вид:
|
|
|
|
x |
2 |
|
|
|
x |
1 |
|
|
|
y |
|
||||||||
x |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
или |
5 |
1 |
5 |
1 |
|
||||||||||||||||||
|
|
T 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
y |
|
y |
|
|
|
|
|
1 |
|
|
|
|
|
2 |
|
|
|
||||||
|
|
1 |
|
y |
|
|
|
|
|
|
x1 |
|
|
|
|
|
|
|
|
y1 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
5 |
|
5 |
||||||||||||||
Подставим в наше уравнение линии и получим:
4x 2 |
9y 2 |
|
8 |
|
x |
|
144 |
|
y |
80 0 |
||
|
|
|
|
|
|
|||||||
1 |
1 |
|
5 |
1 |
5 |
1 |
|
|||||
Сделаем параллельный перенос осей координат. Для этого выделим полные квадраты по х1 и у1:
4(x |
1 )2 9(y 8 )2 |
36 0 |
|
Обозначим |
x |
|
x |
1 |
; y |
|
y |
8 |
. Тогда уравнение |
|||||||||||
1 |
5 |
1 |
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
1 |
5 |
|
2 |
1 |
5 |
|
приобретет вид: 4х22 + 9у22 |
= 36 |
или |
x |
|
2 |
y |
2 |
1 |
|
|
|
|
|
|
|
|
|
|||||||
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
9 |
|
4 |
|
|
|
|
|
|
|
|
|
|
|
||
|
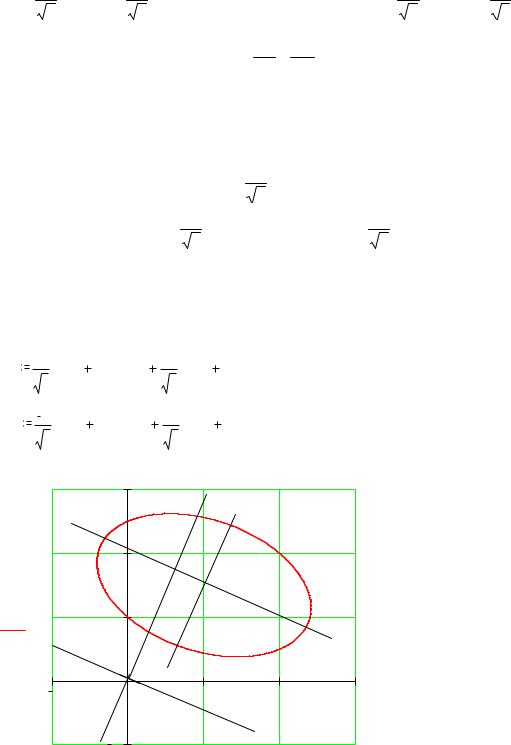
Это эллипс с полуосями 3 и 2. Определим угол поворота осей координат и их сдвиг для того, |
|||||||||||||||||||||||
чтобы построить эллипс в старой системе. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
2 |
|
0,894__ arccos0,894 200 |
|
|
|||||||||||
|
|
cos cos(e i) |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
1 |
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
x |
|
x |
|
1 |
x 0,44___ y |
|
y |
8 |
y |
3,58 |
|
|
||||||||||
|
|
|
2 |
1 |
|
5 |
|
1 |
|
|
|
|
|
2 |
|
|
1 |
5 |
1 |
|
|
|
|
|
Построим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x(t) |
2 (0.44 |
3 cos(t)) |
1 |
(3.58 |
2 sin(t)) |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
5 |
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y(t) |
1 (0.44 |
3 cos(t)) |
2 |
(3.58 |
2 sin(t)) |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
5 |
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y(t) |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
0 |
|
|
|
2 |
|
|
|
4 |
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x(t)
Проверка: при х = 0: |
8у2 - 56у + 80 = 0 |
у2 – 7у + 10 = 0. Отсюда у1,2 = 5; 2 |
При у =0: |
5х2 – 32х + 80 = 0 |
Здесь нет корней, т. е. нет точек пересечения с осью х! |
