
Lineynaya algebra i analitich_geom / Ivleva_i_kurs_lekciy_po_lineynoy_algebre_i_analiticheskoy_ge
.pdf
x1y1 + x2y2 + … + xnyn = 0
вспомним, что это условие ортогональности двух векторов, которое в векторной алгебре мы получим из скалярного произведения.
В пространстве c(a, b) условие ортогональности имеет вид
b
(t) (t)dt 0
a
Например, векторы x = cos nt и y = sin mt, где m и n – целые, ортогональны при a = - и b =
|
|
[sin(n m) sin(n m)]dx 1/2[cos(n m)x cos(n m)x] |
|
|
0 |
||||
|
|||||||||
cosntsin mtdt 1/2 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
n m |
|
n m |
|
|
|
|
|
|
|
|
|
|
||||
С этим важным примером мы будем часто встречаться в математике.
Теперь введем определение: линейное пространство R называется нормированным, если выполнены следующие два требования:
1. любому элементу x пространства ставится в соответствие или определяется норма

 x
x


 (x,x) .
(x,x) .
2.Указанное правило введения нормы подчинено следующим аксиомам: 10 || x || > 0, если x 0; || x || = 0, если x = 0
20 || x || = | | || x ||.
30 справедливо равенство || x + y || || x || + || y || называемое неравенством Минковского или неравенством треугольника.
Всякое евклидово пространство является нормированным, если в нем норму любого элемента х определить равенством 
 x
x


 (x,x) . Первые две аксиомы непосредственно вытекают из аксиом скалярного произведения 30 и 40.
(x,x) . Первые две аксиомы непосредственно вытекают из аксиом скалярного произведения 30 и 40.
Справедливость неравенства Минковского докажем, опираясь на неравенство Коши – Буняковского:
(x, y) 
 (x,x)
(x,x) 
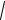 (y, y)
(y, y)

 x y
x y


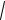 x y,x y
x y,x y 
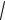 (x,x) 2(x, y) (y, y)
(x,x) 2(x, y) (y, y) 
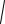 (x,x) 2
(x,x) 2
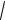 (x,x)
(x,x)
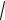 (y, y) (y, y)
(y, y) (y, y) 
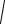 [
[
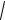 (x,x)
(x,x) 
 (y, y)]2
(y, y)]2 
 (x,x)
(x,x) 
 (y, y)]
(y, y)] 
 x
x


 y
y


Ортонормированный базис конечномерного Евклидового пространства
В линейном пространстве, как мы установили в предыдущих лекциях, существует базис – любые n линейно независимых векторов. Все базисы были одинаковы. В евклидовом пространстве существуют специальные, особо удобные базисы, называемые ортонормированными базисами.
Введем определение ортонормированного базиса: будем говорить, что k элементов e1, e2, … en n –
мерного евклидового пространства Е образуют ортонормированный базис этого пространства, если эти элементы попарно ортогональны и норма каждого из этих элементов равна единице, т.е. если
1 при i k
(ei ,ek )
0 при i k
Существует теорема: во всяком n – мерном евклидовом пространстве E существует ортонормированный базис.
Доказательство: согласно определению размерности в пространстве E найдется n линейно независимых векторов 1, 2, …, n. Докажем, что можно построить n элементов e1, e2, … en, линейно выражающихся через 1, 2, …, n и образующих ортонормированный базис.
Определим вектор e1 как нормированный вектор 1, e1*= 1:
e1 1
 ( 1, 1)
( 1, 1)
построим вектор e2 так, чтобы он был ортогонален вектору e1:
|
|
|
|
|
|
|
|
e2* |
2 |
e1 |
|
|
|
|
|
|
|
||||
умножим скалярно на e1: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
(e*,e ) ( |
2 |
,e ) (e ,e ) |
|
|
|
|
|
|
|
|
|
||||||||||
2 |
1 |
|
|
|
1 |
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|||
(e*,e ) 0; |
|
|
|
( 2 ,e1) |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
2 |
1 |
|
|
|
|
|
|
|
(e1,e1) |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
e* |
|
|
|
( |
2 |
,e ) |
|
|
|
|
|
|
|
|
|
e |
* |
|
|||
|
|
|
|
|
1 |
e |
|
( |
|
,e )e |
e |
|
|
|
|
2 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
2 |
|
2 |
|
(e1,e1) 1 |
2 |
|
|
2 |
1 1 |
|
2 |
|
|
(e2*,e2*) |
|
||||||
Вектор e3 определим следующим образом:
e3* 3 1e1 2e2
Коэффициенты 1 и 2 найдем из условия ортогональности вектора е3 к вектору е1 и вектору
е2:
|
* |
,e1) ( 3,e1) 1(e1,e1) 2 (e2 ,e1) |
(e3 |
||
|
* |
|
|
,e2 ) ( 3,e2 ) 1(e1,e2 ) 2 (e2 ,e2 ) |
|
(e3 |
||

|
|
|
( 3,e1) |
( |
|
,e ) |
|
|
|
|
|||||
отсюда: |
1 |
|
(e ,e ) |
3 |
1 |
||
|
|
1 |
1 |
|
|
|
|
2 ( 3,e2 ) |
|
|
|||||
e |
|
e* |
|
|
, где e* |
|
|
|
,e )e |
|
|
,e |
|
)e |
|
|
|
3 |
|
|
3 |
( |
3 |
( |
3 |
2 |
2 |
||||||
|
|
|
|
|||||||||||||
3 |
|
e*,e* |
3 |
|
1 |
1 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
3 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Продолжая этот процесс n раз, получим для вектора en:
* |
|
|
|
|
n 1 |
|||
en |
|
en |
|
, где en* n |
( n ,en 1)en 1 ... ( n ,e1)e1 |
или en* n |
( 1)( n ,ek )ek |
|
|
|
|
||||||
en* ,en* |
||||||||
|
|
|
|
|
|
k 1 |
||
Т.о. мы доказали теорему, что во всяком пространстве Е существует ортонормированный базис. В процессе доказательства мы построили этот базис. Процесс построения называется ортогонализация или процесс ортогонализации .
В ортонормированном базисе скалярное произведение векторов равно сумме произведений координат этих векторов – этим свойством мы уже пользовались в векторной алгебре:
(x, y) = x1y1 + x2y2 +… + xnyn
Действительно:
(x, y) (x1 |
e1 x2 |
e |
...2 |
xn |
e |
n )(y1 |
e1 y2 |
e |
...2 |
yn |
e |
n ) x1 y1( |
e1 |
...e1) |
xn yn ( |
e |
n |
e |
n ) |
x1 y1 x2 y2 ... xn yn
Ортогональные матрицы и их свойства
Рассмотрим теперь, какими свойствами обладает матрица перехода от одного ортонормированного базиса к другому в евклидовом пространстве. Вспомним перехода от одного базиса к другому: если e1 Ae , то x AT x . Матрицу АТ мы называли матрицей перехода от одного базиса к другому. Столбцы этой матрицы представляют собой координаты векторов en в
базисе en .
Введем сначала определение: матрица Т с вещественными коэффициентами называется ортогональной, если Т’ = T-1 – транспонированная матрица равна обратной. Т.е. Т Т’ = T’ T = E.
Отсюда следует det (T T’) = det T det T’ = det E = 1 или det T = 1.
Обратная матрица T-1 также ортогональна:
(T 1) (T ) T (T 1) 1, или (T 1) (T 1) 1 .
Запишем еще свойства ортогональной матрицы, вытекающие из того, что

T T T 1 T E, или:
n |
n |
|
|
1, |
i j |
tik tkj |
tki tkj |
ij |
|
0, |
i j |
k 1 |
k 1 |
|
|
||
ti21 ti22 ... tin2 |
1 |
|
|
сумма квадратов элементов какой – либо строки (или |
|
или: |
|
|
|
0 |
|
ti1tj1 ti2tj2 ... tintjn |
|
||||
столбца) равна 1, а сумма произведений соответствующих элементов разных строк (столбцов) равна
0.
Предположим, имеем два ортонормированных базиса в евклидовом пространстве: e и e .
Если e1 Ae , то координаты некоторого вектора Х в старом базисе х и новом х’ связаны
соотношением: x A 1x , где АT – матрица перехода.
Теорема: матрица перехода от одного ортонормированного базиса к другому является ортогональной.
Доказательство: положим имеем два вектора
X x1e1 x2e2 ... xnen x1e1 x2e2 ... xnen
Y y1e1 y2e2 ... ynen y1e1 y2e2 ... ynen
Запишем матрицы – столбцы координат этих векторов:
|
|
|
x |
|
|
x |
|
|
|
|
|
y |
|
|
|
|
|
y |
|
|
|
|||
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
||
|
|
|
x2 |
|
|
|
|
|
|
|
y2 |
|
|
|
|
|
|
|
|
|||||
X |
|
X |
x2 |
|
|
Y |
|
Y |
y2 |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
... |
|
|
|
|
|
|
|
|||||||||
|
|
|
... |
|
|
... |
|
|
|
|
|
|
|
|
|
... |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
xn |
|
|
|
|
|
|
yn |
|
|
|
|
|
|
|
|||||||
|
|
|
|
xn |
|
|
|
|
|
|
yn |
|
|
|||||||||||
Скалярное произведение этих двух векторов: |
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(X,Y) x1 y1 |
x2 y2 |
... xn yn |
|
|
|
, или, в матричной записи: |
||||||||||||||||||
x1 y1 |
x2 y2 |
...xn yn |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
( |
|
|
|
) XTY XTY |
|
|
|
|
(*) |
|||||||
|
|
|
|
|
|
|
|
X |
,Y |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
|
|
|
|
Если матрица перехода от одного базиса e к другому e есть S, то:
X = S X1 ; Y = S Y1
Подставим в (*):
X TY (SX1)T SY1 X1T ST SY1 X1TY1
Отсюда ST S = E или ST = S-1. Т.е. матрица S – ортогональная.
К примеру, матрица, осуществляющая поворот осей координат в одной из предыдущих лекций – это матрица перехода от одного ортонормированного базиса к другому. Она является ортогональной.
x x cos y sin |
|
cos |
sin |
|
|
T |
|
|
|
|
cos |
|
||
y x sin y cos |
|
sin |
|
|
detT = 1, T-1 |
|
cos |
sin |
= T` = |
|
|
|
|
|
sin |
|
|
|
cos |
Лекция 13.
Линейные операторы.
Пусть L1 и L2 – линейные пространства, размерности которых соответственно n и m. Будем называть
~
оператором A, действующим из L1 в L2 отображение L1 L2, если задан закон, по которому
каждому вектору x L1 ставится в соответствие единственный вектор y L2. При этом у называется
~ |
~ |
~ |
образом х, а х – прообразом у для оператора A. Обозначаем преобразование у = |
Aх. Оператор |
A |
представляет собой в некотором смысле обобщение известного из анализа определения функции на случай, когда областью задания функции является произвольное линейное пространство L1, а
область значений принадлежит пространству L2.
|
|
~ |
|
Оператор A будем называть линейным, если для любых элементов х1, х2 пространства L1 и любого |
|||
вещественного числа выполняются два условия: |
|||
10 |
~ |
~ |
~ |
A |
(х1 + х2) = A |
х1 + A х2 (свойство аддитивности оператора). |
|
20 |
~ |
~ |
(свойство однородности оператора). |
A |
( х) = A х |
||
Если пространство образов L2 совпадает с пространством прообразов L1, то линейный оператор в этом случае отображает пространство само в себя. Такой оператор называют также линейным преобразованием пространства.
Действия над линейными операторами |
|
|
|
|||
Во множестве всех операторов, действующих из L1 |
в L2 можно определить операции суммы таких |
|||||
операторов и умножения на скаляр: |
|
|
|
|
|
|
~ |
~ |
~ |
~ |
~ |
~ |
~ |
а) суммой двух операторов A и |
B назовем оператор ( A |
+ B), для которого ( A |
+ B) х = |
Aх + |
||
~ |
|
|
|
|
|
|
Bх; |
|
|
|
|
|
|
~ |
|
|
~ |
|
~ |
~ |
б) произведением оператора A |
на скаляр назовем оператор A, для которого ( A) х = ( A х); |
|||||
в) нулевым оператором 0 назовем оператор, который действует по правилу 0 х = 0 для любого х;
|
~ |
~ |
г) для каждого оператора A |
определим противоположный оператор - A посредством соотношения - |
|
~ |
~ |
|
A |
= (-1) A. |
|
Тогда множество всех линейных операторов М(L1, L2) с указанными выше операциями и с выбранными нулевым и противоположным оператором образует, очевидно, линейное пространство.
Рассмотрим свойства множества операторов М(L,L), т.е. операторов, действующих из L в L (пространство само в себя).
Назовем единичным оператор I~, действующий по правилу I~х = х. |
|
|
||||||
|
|
|
|
|
|
~ |
~ |
|
Введем понятие произведения линейных операторов из множества М(L, L) A |
и B по правилу: |
|||||||
~ ~ |
~ |
~ |
~ ~ |
~ |
~ |
|
|
|
( A B) х = A(Bх ). Отметим, вообще говоря, что |
A B |
B |
A. |
~ |
|
|||
|
|
|
|
|
|
|
|
|
Введя эти два определения, можно определить обратный оператор для данного оператора A: если |
||||||||
~ ~ |
~ |
~ |
~ |
|
|
|
|
|
A B |
=B |
A=I . |
|
|
~ |
~-1 |
|
|
|
|
|
~ |
|
|
|
||
В этом случае оператор B называется обратным оператору |
A и обозначается |
A . |
|
|||||
|
|
|
~ |
|
|
|
~ |
~ |
Из определения оператора A-1 следует, что для любого х V выполняется соотношение A-1 |
Aх = |
|||||||
х.
~
Будем говорить, что линейный оператор A действует взаимно однозначно, из L в L, если любым
~ ~
двум различным х1 и х2 отвечают различные Aх1 и Aх2.
~
Отметим без доказательства, что для того, чтобы линейный оператор A из М(L, L) имел обратный,
необходимо и достаточно, чтобы этот оператор действовал взаимно однозначно из L в L.
Введем понятие ядра и образа линейного оператора.
~
Ядром линейного оператора A называется множество всех тех элементов х пространства L, для
~
которых Aх = 0.
|
~ |
|
|
|
|
Ядро обозначается символом ker A. (привести пример – система линейных однородных уравнений). |
|||||
~ |
~ |
|
|
|
|
Если ker A = 0, то оператор A действует взаимно однозначно из L в L. Действительно, в этом |
|
||||
~ |
~ |
~ |
~ |
~ |
~ |
случае если A |
х = 0, то х = 0. Или у1 = Aх1, у2 = |
Aх2. Если у1 = у2, то у1 – у2 = 0 = |
Aх1 - |
Aх2 = |
A(х1 |
– х2) х1 – х2 = 0. |
|
|
|
|
|
~ |
|
|
~ |
|
|
Условие ker A |
= 0 является необходимым и достаточным для того, чтобы оператор A имел |
|
|||
обратный.
~
Образом линейного оператора A назовем множество всех элементов у пространства L,
~
представляемых в виде у = Aх.
~ |
|
Образ обозначается символом im A (отличается от Im, используемого для обозначения мнимой |
|
части z). |
|
~ |
~ |
Очевидно, что если ker A = 0, то im |
A = L и наоборот. Очевидно, что ядро и образ линейного |
~ |
|
|
оператора A являются линейными подпространствами пространства L. Поэтому можно говорить о |
||
|
~ |
~ |
размерности dim (ker A) и dim (im |
A). |
|
Запишем без доказательства следующую теорему: |
||
|
|
~ |
Пусть размерность пространства L равна n и пусть A - линейный оператор из M(L, L). Тогда dim |
||
~ |
~ |
|
(ker A) + dim (im |
A) = n. |
|
Матрица линейного оператора.
|
|
|
|
|
|
|
|
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
|
|
|
|
Пусть задан линейный оператор A, переводящий x L1 |
в y L2: |
y |
Ax |
. |
|
|
|||||||||||||||||||||||||||||||
Выберем в L1 базис e1 e2 … en и в L2 базис g1 g2 … gm |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
x |
x1 |
e1 x2 |
e |
2 |
|
... xn |
e |
n |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
y |
y1 |
g |
1 |
y2 |
g |
2 ... ym |
g |
m |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
|
|
~ |
|
|
~ |
|
||||
y y1 |
g |
1 y2 |
g |
2 ... yn |
g |
n A(x1e1 x2e2 |
... xnen ) x1Ae1 |
x2 Ae2 |
... xn |
Aen . |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
~ |
Т.е. для задания оператора достаточно задать только образы базисных векторов, т.е. Aе1, |
Aе2, …, |
||||||||||||||||||||||||||||||||||||
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Aеn. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Положим, что эти образы есть |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
~ |
a11g1 |
a12 g2 |
... a1m gm |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
Ae1 |
|
|
|
|
n AT |
|
|
m |
|
|
|
|
|
|
|
|
|||||||||||||||||||
... |
|
|
|
|
|
|
|
|
|
|
|
|
e |
g |
|
|
|
|
|
|
|
|
|||||||||||||||
~ |
an1g1 |
an2 g2 |
... anm gm |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
Aen |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Составим матрицу: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
a |
|
|
... |
|
|
a |
n1 |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11 |
|
|
21 |
|
... |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
A |
a12 |
a22 |
|
|
an2 |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
... ... |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
... ... |
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
a |
2m |
... |
|
|
a |
nm |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1m |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
Ae1 |
Ae |
2 |
Ae |
n |
|
|
|
|||||||||||||||||||
|
Тогда из вышесказанного следует: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
y1 a11x1 a21x2 |
... an1xn |
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
... |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
ym a1m x1 a2m x2 ... anmxn |
|
|
|
||||||||||||||||||||||||
|
или |
|
Y = A X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Матрица А, транспонированная АT называется матрицей линейного оператора, k-й столбец
~
этой матрицы составлен из координат вектора Aеk в базисе g1 g2 … gm.
Оказывается, что некоторые характеристики этой матрицы не зависят от базисов и характеризуют внутренние свойства оператора. Так, запишем без доказательства, что ранг матрицы линейного оператора равен размерности пространства образов. Будем называть этот ранг – рангом линейного оператора. Если этот ранг совпадает с размерностью пространства L, или размерность
~
пространства образов совпадает с размерностью пространства прообразов, то оператор A назовем невырожденным.
Если множество образов и множество прообразов принадлежат одному и тому же пространству, то будем говорить о преобразовании пространства само в себя а оператор этого преобразования будем называть оператором линейного преобразования или линейный оператор. В
дальнейшем мы будем рассматривать линейные операторы и употреблять термин операторы.
Изменение матрицы линейного оператора
при переходе от одного базиса к другому.
Мы уже упоминали, что матрица линейного оператора зависит от базиса. Рассмотрим вопрос
~
озависимости матрицы от базиса в общем случае. Пусть задан оператор у = Aх.
Внекотором базисе {e} ему соответствует линейное преобразование Y = AX.
Введем новый базис {e*}. Если матрица перехода есть Т, то X = TX* |
Y = TY*. |
|
||
Отсюда имеем TY* = ATX*; Y* = T-1ATX*. |
|
|
|
|
Или Y* = A*X*; |
A* = T-1AT. |
|
|
|
Отметим, что матрицы А и А* называются подобными (Т – невырожденная матрица). |
||||
|
Собственные числа и собственные векторы |
|
|
|
|
линейного преобразования. |
|
|
|
Ненулевой вектор х назовем собственным |
вектором линейного |
оператора |
~ |
|
A, если |
||||
существует такое число , что выполняется равенство: |
~ |
|
|
|
Aх = х. |
|
~ |
||
|
|
|
|
|
Число называется собственным числом или собственным значением оператора A. |
||||
Т.к. оператор |
~ |
само в себя, то матрица этого |
оператора |
|
A преобразует пространство |
||||
квадратная. Если базис пространства {en}, то
~
Ae1 a11e1 a12e2 ... a1nen
...
~
Aen an1e1 an2e2 ... annen
матрица оператора:
|
a |
a |
|
... |
|
11 |
|
21 |
|
A |
a12 |
a22 ... |
||
|
|
|
|
|
|
... ... ... |
|||
|
a |
a |
2n |
... |
|
1n |
~ |
|
|
|
~ |
|
|
|
|
Ae1 |
Ae2 |
|
|
~
Запишем в координатной форме равенство Aх = х:
an1 an2
...
ann
~
Aen
~ |
|
|
|
|
|
|
|
|
|
|
|
|
( A - Е) х = 0 |
|
|
|
|
|
|
||||||
(a11 )x1 |
a21x2 |
... a1n xn |
0 |
|||||||||
|
|
|
(a22 )x2 |
... a2n xn |
0 |
|||||||
a21x1 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
... |
|
|
|
|
|
|
|
|
|
|
|
|
a |
n1 |
x |
a |
n2 |
x |
2 |
... (a |
nn |
)x |
n |
0 |
|
|
1 |
|
|
|
|
|
|
|||||
Эта система линейных однородных уравнений относительно координат искомого вектора х.
Т.к. х 0, то системы должна иметь ненулевое решение. Значит, для этого, должно быть det ( A - E ) = 0, или
|
a11 |
a21 |
... |
an1 |
|
( ) |
a12 |
a22 |
... |
an2 |
0 |
|
... |
... |
... |
... |
|
|
a1n |
a2n |
... |
ann |
|
Уравнение ( ) = 0 называется характеристическим уравнением для линейного оператора
~
A, а многочлен
n
( ) det(A E) dk k
k 0
степени n относительно - характеристическим многочленом.
По основной теореме алгебры, каждый многочлен степени n имеет n корней с учетом их кратности. Значит, характеристическое уравнение имеет по крайней мере один корень, т.е. каждый оператор имеет хотя бы один собственный вектор. Правда в вещественном пространстве многочлен может не иметь вещественных корней и поэтому в нашем линейном пространстве не каждый
линейный оператор имеет собственные векторы.
Т.о. для нахождения собственного вектора надо составить характеристический многочлен,
найти все его корни, которые будут собственными числами. После этого нужно каждое собственное число i подставить вместо в систему и найти все ее линейно – независимые решения. Число таких решений есть n – ri, где ri – ранг матрицы A - iE. Отсюда следует, что размерность пространства
собственных векторов, соответствующих одному собственному числу i равна n – ri.
Вспомним, что матрица линейного оператора изменяется при изменении базиса:
A* = T-1AT.
Найдется ли такой базис, в котором матрица А* имела бы диагональный вид? Справедлива следующая теорема: для того, чтобы матрица А в данном базисе {ek} была диагональной,
необходимо и достаточно, чтобы базисные векторы ek |
были собственными векторами этого |
оператора. |
|
Доказательство: пусть ek являются собственными векторами оператора А. Тогда |
|
Aek = kek |
(*) |

А отсюда матрица А необходимо имеет вид
|
|
0 |
|
0 |
|
|
2 |
|
|
A |
0 |
|
0 |
0 0 n
и наоборот. Пусть А – диагональная матрица оператора А в данном базисе {ek}. Тогда соотношнния
Aek = 11e1+ 12e2+ 1nen (k = 1,…,n)
примут вид (*), а это значит, что ek - собственные векторы.
Запишем без доказательства свойство линейного оператора: собственные векторы линейного
оператора, отвечающие различным собственным значениям, линейно независимы.
Определение: назовем оператор А, матрица которого приводится к диагональному виду,
оператором простой структуры. Запишем без доказательства, что оператор имеет простую
структуру в двух случаях: 1) характеристический многочлен имеет n различных корней; 2) для каждого корня i кратности ki ранг матрицы (A- iE) был равен n-ki.
Рассмотрим, чему равен определитель матрицы линейного оператора А при смене базиса. det(A*) = det(T-1AT) = det(T-1)det(A)det(T) = det(A)det(T-1T) = det(A)det(E) = det(A)
Таким образом, можно сделать вывод, что величина определителя матрицы линейного оператора не зависит от выбора базиса. Для поиска собственных чисел линейного оператора мы составляли характеристический многочлен
n
( ) det(A E) dk k
k 0
Поскольку величина определителя не зависит от выбора базиса, то величины dk являются инвариантами – не зависят от базиса. Принято называть коэффициент при n-1 : dn-1 = a11+a22+…+ann
следом оператора А и обозначать trA (trace – след).
trA = a11+a22+…+ann = 1+ 2+ n.
Нетрудно проследить связь между инвариантами преобразования систем координат, с
которыми мы сталкивались при преобразовании уравнений поверхностей второго порядка:
I1 a11 a22 a33 trA |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
I |
2 |
|
|
a11 |
a12 |
|
|
|
a22 |
a23 |
|
|
|
a33 |
a31 |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
a |
21 |
a |
22 |
|
|
|
a |
32 |
a |
33 |
|
|
|
|
a |
a |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
13 |
|
11 |
|
|
|
|
||||||
|
|
|
|
a11 |
a12 |
|
a13 |
|
|
|
|
|
|
|
|
a11 |
a12 |
a13 |
a14 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
a12 |
a22 |
a23 |
a24 |
||||||||||||||
I |
3 |
|
a |
21 |
a |
22 |
|
a |
23 |
|
I |
4 |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
a |
23 |
a |
33 |
a |
34 |
||||||
|
|
|
|
a31 |
a32 |
|
a33 |
|
|
|
|
|
13 |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
a14 |
a24 |
a34 |
a44 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
