
Lineynaya algebra i analitich_geom / Ivleva_i_kurs_lekciy_po_lineynoy_algebre_i_analiticheskoy_ge
.pdf
или гиперболу, если е 1. При этом точка F называется фокусом, а прямая D – директрисой
рассматриваемого места точек.
Лекция 8.
Плоскость. Различные ее виды
Прежде всего, в математике доказывается, что если в пространстве задана произвольная
плоскость и декартова система координат, то уравнение этой плоскости является уравнением
первой степени.
Мы докажем, что если в пространстве фиксирована произвольная система координат Oxyz, то всякое уравнение первой степени с тремя переменными x, y, z определяет относительно этой системы плоскость.
Доказательство: рассмотрим произвольное уравнение первой степени:
A x + B y + C z + D = 0,
Где хотя бы одно из A B C отлично от 0. Тогда это уравнение имеет хотя бы одно решение:
к примеру A x0 + B y0 + C z0 + D = 0 |
|
|
|
Тогда вычитая одно из другого, получим эквивалентное уравнение: |
|
|
|
A (x - x0) + B (y - y0) + C (z - z0) = 0. |
(*) |
|
|
Для доказательства нашего утверждения достаточно доказать, что уравнение (*) определяет |
|||
плоскость, проходящую через точку M(x0 y0 z0) и перпендикулярную вектору |
n |
A,B,C . |
|
В самом деле, если точка M(x y z) лежит на указанной |
плоскости, то вектор |
||
M0 M {x x0; y y0;z z0} ортогонален вектору n и их скалярное произведение равно 0. Если
же точка не лежит в указанной плоскости, то вектор M0 M не перпендикулярен n и скалярное произведение не равно 0. Т.о. уравнение (*) (произвольное!) действительно определяет плоскость.
Уравнение A x + B y + C z + D = 0 называется общим уравнением плоскости, а вектор n - нормальным вектором плоскости. Общее уравнение плоскости называется неполным, если какойлибо коэффициент может и не один, равен нулю. К примеру:
D = 0 : A x + B y + C z = 0
Определяет уравнение плоскости, проходящей через начало координат.
С = 0 : A x + B y + D = 0 – плоскость, параллельная оси Z, так как n A,B,0 - n OZ
A = 0 , B = 0 : C z = 0 – плоскость, параллельная XOY и т.д. Всего 10 вариантов. Если уравнение полное, то его можно свести к уравнению плоскости в отрезках:
x |
y |
z |
x y z |
||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|||
|
D |
|
D |
|
D |
a |
b |
c |
|||||||||
A |
|
|
B |
|
|
C |
|
|
|
|
|
|
|
|
|||
Ясно, что a, b, c – это отрезки, отсекаемые плоскостью на осях координат. Действительно, если y = z = 0, то x = a – определяет точку пересечения плоскости с OX.
Угол между двумя плоскостями.
Из определения скалярного произведения можно получить для угла между плоскостями, заданными общими уравнениями величину:
A1x B1x C1x D1 0 |
|
|
|
A A B B C C |
2 |
|
|
|
||||||
|
0 |
cos |
|
|
1 |
2 |
1 |
2 |
1 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|||
A 2 |
B 2 |
C 2 |
|
|
A |
2 B |
|
C 2 |
|
|||||
A2 x B2 x C2 x D2 |
|
|
|
|
2 |
|
||||||||
|
|
1 |
1 |
1 |
|
|
2 |
|
2 |
2 |
|
|||
Условие параллельности: A1 B1 C1
A2 B2 C2
Условие перпендикулярности: A1 A2 B1B2 C1C2 0
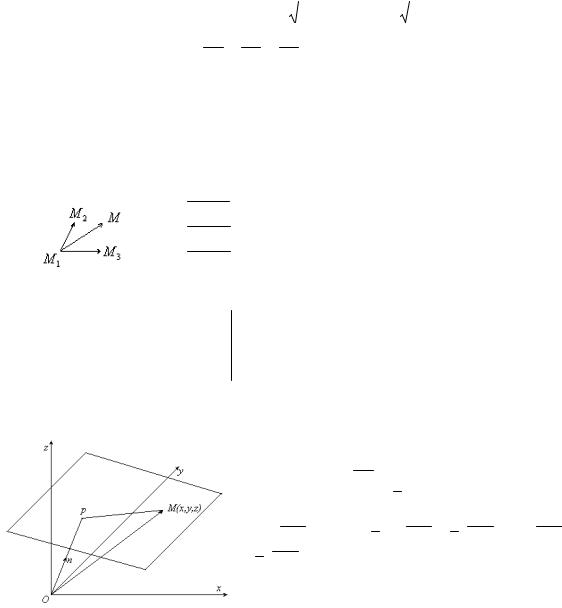
Уравнение плоскости, проходящей через три заданные точки
Точка M(x,y,z) лежит на плоскости. Значит три вектора компланарны:
M1 M1 {x x1;y y1;z z1} M1 M2 {x x2 ;y y2;z z2}
M1 M3 {x x3;y y3;z z3}
Уравнение плоскости получится из условия компланарности трех векторов, а именно: смешанное произведение трех векторов равно нулю:
x x1 |
y y1 |
z z1 |
|
x2 x1 |
y2 y1 |
z2 z1 |
0 |
x3 x1 |
y3 y1 |
z3 z1 |
|
Нормированное уравнение плоскости. Отклонение точки от плоскости.
Поставим цель выразить уравнение плоскости через
длину отрезка OP= р и направляющие косинусы единичного вектора n . Очевидно, точка М лежит на
нужной нам плоскости тогда и только тогда, когда
прn OM p или nпрn OM n OM прn OM , но: n OM xcos ycos zcos и тогда уравнение
искомой плоскости, очевидно будет: xcos ycos zcos p 0.
Так же как и в случае уравнения линии, назовем отклонением точки М от плоскости ее расстояние до плоскости со знаком (-), если точка М и начало координат лежат в одной стороне от плоскости и со знаком (+), если по разные стороны. Тогда можно доказать, что для нахождения отклонения точки М от плоскости необходимо в левую часть нормированного условия плоскости подставить на место x, y и z координаты x0 y0 z0 точки М0.
Как привести уравнение плоскости к нормированному виду. Поскольку
Ax Bx Cx D 0
xcos ycos zcos p 0

одна и та же плоскость, то, очевидно, найдется такое число t, что:
t A = cos ; t B = cos ; t C = cos ; t D = -p ;
1
Из первых трех уравнений имеем: |
t |
|
|
|
|
|
, отсюда расстояние плоскости от |
||||||||
|
|
|
|
|
|||||||||||
|
A2 |
B2 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
C2 |
||||
начала координат |
|
|
D |
|
|
|
|
|
. |
Из |
четвертого равенства, поскольку p всегда |
||||
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
||||||||
A2 B2 |
|
|
|||||||||||||
|
|
C2 |
|
|
|
|
|
|
|||||||
положительно, следует знак у t брать противоположный D.
Уравнение пучка плоскостей.
Определение: совокупность всех плоскостей, проходящих через одну и ту же прямую L,
называется пучком плоскостей. Существует следующее утверждение: если
A1 x + B1 y + C1 z + D1 = 0
A2 x + B2 y + C2 z + D2 = 0
Условия двух непараллельных плоскостей, пересекающихся по некоторой линии L, а и -
какие угодно, неравные нулю числа, то
(A1 x + B1 y + C1 z + D1 ) + (A2 x + B2 y + C2 z + D2 ) = 0
Это уравнение определяет плоскость, проходящую через прямую L, а при произвольных и –
пучок плоскостей.
Уравнение связки поверхностей – т.е. поверхностей, проходящих через заданную точку, есть,
очевидно: A (x – x0) + B (y – x0) + C (z– x0) = 0.
Прямая линия в пространстве.
Мы уже определили прямую линию, как пересечение двух плоскостей:

A1 x + B1 y + C1 z + D1 = 0
A2 x + B2 y + C2 z + D2 = 0
Теперь определим уравнение линии в пространстве как уравнение прямой, проходящей через
заданную точку (x1 y1 z1) и имеющей заданное направление: q {l,m,n}. Очевидно, векторы
M1 M {x x1,y y1,z z1} и n {l,m,n} должны быть коллинеарны.
Условие коллинеарности двух векторов:
x x1 y y1 z z1 l m n
Это и есть каноническое уравнение прямой в пространстве. Отсюда легко вывести уравнение прямой, проходящей через две заданные точки. Действительно, искомая прямая должна быть коллинеарна вектору x2 - x1; y2 - y1; z2 - z1, т.е.
x x1 |
|
y y1 |
|
z z1 |
||||||
|
|
|
||||||||
x |
2 |
x |
|
y |
2 |
y |
|
z |
2 |
z |
|
1 |
|
|
1 |
|
|
1 |
|||
Параметрическое уравнение прямой в пространстве.
Примем за параметр |
x x1 |
|
y y1 |
|
z z1 |
t , тогда |
|
l |
m |
n |
|||||
|
|
|
|
x = x1 + l t
y = y1 + m t
z = z1 + n t
Если t – время, то эти уравнения представляют собой движение материальной точки в
пространстве. Если вам знакомы производные, то Vx| = l ; Vy| = m ; Vz| = n.
V 
 Vx2 Vн2 Vя2
Vx2 Vн2 Vя2 
 l2 m2 n2
l2 m2 n2

Угол между двумя прямыми есть очевидно угол между направляющими векторами n1 и n2
cos |
|
|
l1l2 m1m2 n1n2 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
l2 |
m2 |
n2 |
|
l2 |
m2 |
n2 |
|
||
|
|
|
|
||||||
1 |
1 |
1 |
2 |
2 |
2 |
|
|||
Условие перпендикулярности: l1 l2 + m1 m2 + n1 n2 = 0.
Условие параллельности: |
l1 |
|
m1 |
|
n1 |
||
|
m |
|
|||||
|
l |
2 |
|
|
n |
2 |
|
|
|
2 |
|
|
|||
Условие принадлежности двух прямых к одной плоскости.
Две прямые заданы каноническими уравнениями:
|
x x1 |
|
|
y y1 |
|
z z1 |
и |
x x2 |
|
|
y y2 |
|
z z2 |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
l |
m |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
n |
l |
2 |
|
|
|
|
|
m |
|
|
n |
2 |
|
|
|
|
|
|
|
|||||
1 |
|
1 |
1 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
||||||
Очевидно, |
|
необходимо |
|
|
|
|
и |
|
|
достаточно, |
чтобы |
три |
вектора |
|||||||||||||||
|
|
{x2 |
x1;y2 y1;z2 |
z1}; |
q1 |
{l1,m1,n1} |
q |
2 |
{l2 ,m2 ,n2} были коллинеарны: |
|
||||||||||||||||||
|
M2 M1 |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 x1 |
|
y2 y1 |
z2 z1 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l1 |
|
|
m1 |
n1 |
0 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l2 |
|
|
m1 |
n1 |
|
|
|
||||
Угол между прямой и плоскостью.
Плоскость задана общим уравнением: |
A1 x + B1 y + C1 z |
||||||
+ D1 = 0 , а прямая – |
каноническим уравнением: |
||||||
|
x x1 |
|
y y1 |
|
z z1 |
|
|
|
|
|
|
|
|||
l m n
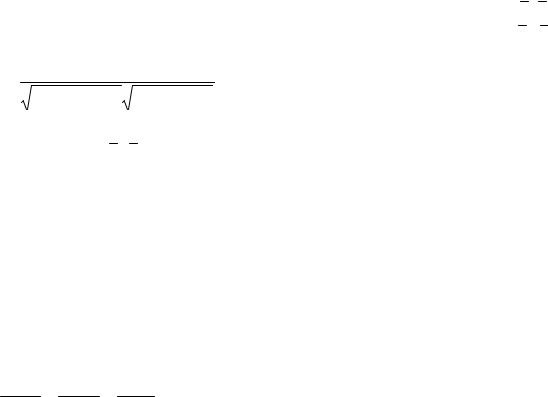
Нам нужно найти угол . Из чертежа ясно, что + = 90 , т.е. cos = sin , но cos |
|
q |
|
n |
, |
|
|
|
|
||
|
|
q |
|
n |
|
|
|
|
|
|
|
Al Bm Cn
или sin
A2 B2 C2 l2 m2 n2
Условие параллельности: |
n |
|
q |
|
cos 0 A l + B m + C n = 0 |
|||||
Условие перпендикулярности: |
|
A |
|
B |
|
C |
|
|||
|
l |
m |
n |
|||||||
|
|
|
|
|
|
|
||||
Условие принадлежности прямой к плоскости.
Прямая: x x1 y y1 z z1 l m n
Плоскость: A x + B y + C z + D = 0
Очевидно, что координаты точки x1 y1 z1 должны удовлетворять уравнению плоскости:
A x1 + B y1 + C z1 + D = 0
И условие параллельности прямой и плоскости должно выполняться:
A l + B m + C n = 0
Эти два условия определяют принадлежность прямой к плоскости.
Рассмотрим некоторые примеры задач на прямую и плоскость в пространстве.
1). Условия пересечения трех плоскостей в одной точке:

A1x B1 y C1z D1 0A2 x B2 y C2 z D2 0
A3 x B3 y C3z D3 0
Очевидно, для единственности решения необходимо и достаточно, чтобы определитель
A1 B1 C1
A2 B2 C2 0.
A3 B3 C3
2). Уравнение прямой, проходящей через данную точку M1(x1 y1 z1) и перпендикулярную данной
плоскости A x + B y + C z + D = 0.
Т.к. направляющим вектором некоторой прямой |
является вектор |
n |
{A,B,C}. Тогда |
|||||
каноническое уравнение искомой прямой есть |
x x1 |
|
y y1 |
|
z z1 |
. |
||
A |
B |
|
||||||
|
|
|
C |
|||||
3). Уравнение плоскости, проходящей через заданную точку M0(x0 y0 z0) и перпендикулярной
заданной прямой x x1 y y1 z z1 : l m n
Вспомним уравнение связки плоскостей, т.е. уравнение всех плоскостей, проходящих через точку x0 y0 z0:
A (x – x0) + B (y – x0) + C (z– x0) = 0.
Искомая плоскость в качестве нормали имеет направляющий вектор заданной прямой
q {l,m,n}. В итоге получаем уравнение: l (x – x0) + m (y – x0) + n (z– x0)=0.
4). Уравнение плоскости, проходящей через данную прямую |
x x1 |
|
y y1 |
|
z z1 |
и через |
l |
m |
|
||||
|
|
|
n |
|||
точку, не лежащую на этой прямой M0(x0 y0 z0). |
|
|
|
|
|
|
Искомая плоскость принадлежит связке: A (x – x0) + B (y – x0) + C (z– x0) = 0.
С другой стороны, этому уравнению должны удовлетворять координаты точки x1, y1, z1:

Ax1 By1 Cz1 D 0
Вспомним условие принадлежности прямой к плоскости:
Al Bm Cn 0
A(x1 x0 ) B(y1 y0 ) C(z1 z0 ) 0
Иполучим в итоге: Al Bm Cn 0
Отсюда, выразив два коэффициента из А В С через третий, можно найти уравнение плоскости.
Другой способ: |
найти векторное произведение C |
направляющего вектора q {l,m,n) и |
вектора M0M1 |
{(x1 x0 ),(y1 y0 ),(z1 z0 )} |
C q M0M1 Координаты этого вектора |
будут, очевидно, координатами нормального вектора к искомой плоскости. Для окончательного написания уравнения плоскости необходимо использовать уравнение связки плоскостей - плоскостей, проходящих через точку М0.
Cx (x x0 ) Cy (y y0 ) Cz (z z0 ) 0
5). Уравнение перпендикуляра, опущенного из заданной точки M0 на данную прямую L1.
Искомый перпендикуляр – это линия пересечения двух плоскостей: 1) плоскость, проходящая через точку M0 и прямую L1 – предыдущий пример и 2) плоскость, проходящая через M0 и
перпендикулярную L1 – это задача № 3. Решая совместно эти два условия, найдем искомое
уравнение прямой.
Другой способ: построить плоскость , проходящую через точку М0 и перпендикулярную
прямой L1. Далее найти точку пересечения плоскости и прямой L1. Предположим, это будет
некоторая точка С. Искомым расстоянием будет длина вектора CM0 .
6). Нахождение расстояния от данной точки M0 до данной прямой L1.
Надо совместно решить уравнения прямых L1 и L2 – это уравнение перпендикуляра из
предыдущей задачи № 5, таким образом найдем координаты точки пересечения прямых L1 и L2 -
основания перпендикуляра M2. Расстояние – это модуль вектора M0 M2 .
Другой путь решения задачи:
L1: |
x x1 |
|
y y1 |
|
z z1 |
q={l,m,n} |
|
l |
m |
n |
|||||
|
|
|
|
Расстояние от точки М0 до прямой L1 есть площадь
параллелограмма q M1 M0 деленная на основание q:
q M1 M0
d
q
7) Найти расстояние между двумя скрещивающимися прямыми:
L1: |
x x1 |
|
y y1 |
|
z z1 |
L2: |
x x2 |
|
y y2 |
|
z z2 |
||
|
|
|
|||||||||||
l |
m |
n |
|
m |
|
||||||||
|
|
|
|
l |
2 |
|
|
n |
2 |
||||
|
1 |
|
1 |
1 |
|
|
|
2 |
|
|
|||
Расстояние равно объему параллелепипеда,
построенного на сторонах q1, q2, M1M2, деленному на
площадь основания
d q1q2 M1 M2 q1 q2
Лекция 9.
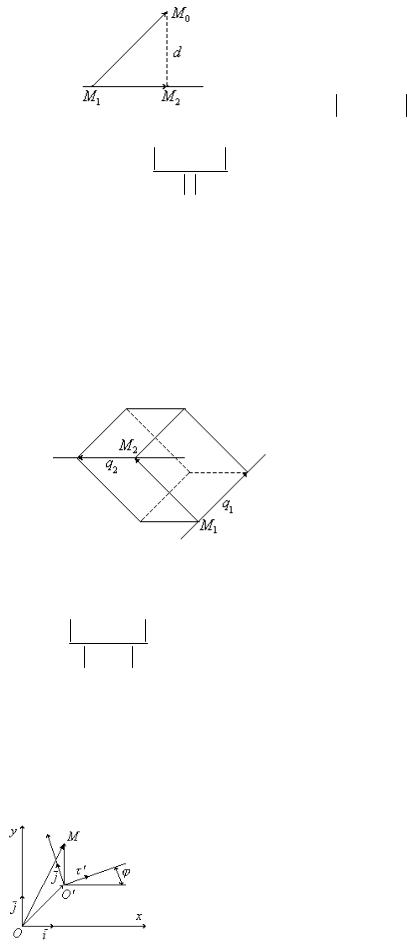
Преобразование декартовых прямоугольных координат на плоскости и в пространстве
Пусть на плоскости заданы две произвольные декартовы
прямоугольные системы координат. Первая определяется началом О и

базисными векторами i j , вторая – центром О’ и базисными векторами i’ j’.
Поставим цель выразить координаты x y некоторой точки М относительно первой системы координат через x’ и y’ – координаты той же точки относительно второй системы.
OM xi yj
Заметим, что |
|
|
|
|
O M x i y j |
||
Обозначим координаты точки О’ относительно первой системы через a и b:
OO ai bj
Разложим векторы i’ и j’ по базису i j:
i 11i 12 j
j 21i 22 j
(*)
Кроме того, имеем: OM OO O M . Введем сюда разложения векторов по базису i’ j’:
xi yj x ( 11i 12 j) y ( 21i 22 j) ai bj (a 11x 21 y )i (b 12 x 22 y ) j
отсюда
x a 11x 21y y b 12 x 22 y
Можно сделать вывод: каковы бы ни были две произвольных декартовы системы на плоскости,
координаты любой точки плоскости относительно первой системы являются линейными функциями координат той же точки относительно второй системы.
Умножим скалярно уравнения (*) сначала на i, затем на j:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i i |
11ii 12ij; |
11 cos(i ^i) |
|
|
|
|
|
(**) |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
21 |
cos( j ^i); |
12 cos(i ^ j); |
22 |
cos( j ^ j) |
|||||||||||||||||||||
Обозначим через угол между векторами i и i’. Система координат i j может быть совмещена с системой i’j’ путем параллельного переноса и последующего поворота на угол . Но здесь возможен и дугой вариант: угол между базисными векторами i i’ также , а угол между базисными векторами j’j’ равен - . Эти системы нельзя совместить параллельным
переносом и поворотом. Необходимо еще и изменить направление оси у на противоположное.
Из формулы (**) получаем в первом случае:
