
Lineynaya algebra i analitich_geom / Ivleva_i_kurs_lekciy_po_lineynoy_algebre_i_analiticheskoy_ge
.pdf
0 ,0 2
Полярные координаты легко преобразовать в декартовые, если направить ось Х вдоль полярной оси и совместить полюс с началом координат. Очевидно:
x*cos
y*sin
и_далее

 x2 y2 ,tg y / x
x2 y2 ,tg y / x
По этим формулам легко переходят от полярных координат к декартовым и наоборот. Так, уравнение окружности радиуса R в полярных координатах есть =R. Пусть, например, линия в полярной системе координат имеет уравнение%
|
|
1/(1 sin ) |
|
|
|
|
|
|
|
|
|
|
отсюда: |
|
|
|
Это парабола |
|
|
|
|
|
|
*sin 1,или, |
x2 y2 |
y 1 |
|
|
|
|||
|
|
|
|
|
|
|
||||
|
|
x2 y2 1 2* y y2 ,y x2 / 2 1/ 2 |
|
|
|
|
||||
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
120 |
90 |
60 |
|
5 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
||
|
0 |
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
150 |
|
|
30 |
|
f(x) |
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
180 |
0 |
|
0 |
0 |
||
|
|
|
|
|
|
|
|
|||
|
4 |
|
|
|
|
210 |
|
|
330 |
|
5 |
|
|
|
|
|
240 |
|
300 |
|
|
|
5 |
0 |
5 |
|
|
270 |
|
|
||
|
5 |
x |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
Определение: линия называется алгебраической, если функция Ф(х,у) представляет собой
алгебраический полином, т.е сумму конечного числа слагаемых вида
alk xl yk
Можно доказать, что если на плоскости задана произвольная прямая линия, и задана декартова система координат Оху, то прямая L определяется в этой системе координат уравнением первой степени. Иначе Ф(х,у)=Ах+Ву+С полином первой степени. Само доказательство мы опустим.
Докажем теперь, что если на плоскости фиксирована произвольная система координат Оху, то всякое уравнение первой степени с двумя переменными х,у определяет прямую относительно этой системы.
В самом деле, пусть задано уравнение
Ax + By + C = 0 |
(**) |

где из А, В, С хотя бы одно не ноль.
Уравнение (**) заведомо имеет хотя бы одно решение х0 у0 (вспомним теорему КронеккераКапелли) или:
Ax0 + By0 + C=0 |
(***) |
Вычитая из (**) уравнение (***), получим уравнение |
|
A (x - x0) + B (y - y0)=0
Докажем, что это уравнение определяет прямую L, проходящую через точку х0,у0 и перпендикулярную вектору n {A,B}.
В самом деле, если точка М( х,у ) лежит на L, то ее координаты удовлетворяют уравнению (***), ибо в этом случае векторы n {A,B}
ортогональны и их скалярное произведение А(х - х0) + В(у - у0)
равно нулю. Если же точка М( х,у ) не лежит на указанной прямой, то векторы n {A,B} и ММ0 не
ортогональны и их скалярное произведение не равно нулю. Уравнение
Ax + By + C = 0
называется общим уравнением прямой. Вектор
n {A,B}
называется нормальным вектором прямой (**).
Уравнение прямой в отрезках
Уравнение (**), где все А, В, С отличны от нуля, можно привести к виду:
|
|
|
|
|
|
|
x |
|
|
y |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|||
|
|
|
|
|
|
|
a |
b |
|
|
|
|
||||||||
Действительно, |
A |
x |
B |
y 1 0; |
x |
|
|
|
y |
|
1; |
a |
C |
;b |
C |
|||||
|
|
|
C |
|
|
|
C |
|
A |
B |
||||||||||
|
C C |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
B |
|
|
|
|
|
|
||||
Числа а и b имеют простой геометрический смысл: это отрезки осей координат, которые отсекает прямая линия, удовлетворяющая этому уравнению.
|
|
у |
|
Действительно, при х = 0 : |
|
|
1;y b |
|
b |
||
при у = 0 : |
х = а |
||
Каноническое уравнение прямой
Определим направляющий вектор прямой, как ненулевой вектор, параллельный данной
прямой. Поставим задачу: найти уравнение прямой, проходящей через заданную точку |
М1(х1 ; |
у1) и имеющей направляющий вектор q {l,m}. |
|
Очевидно, что точка М(х; у) лежит на указанной прямой, если векторы |
ММ1 = |
{x x1;y y1} и q {l,m} коллинеарные, т.е. их координаты пропорциональны: |
|
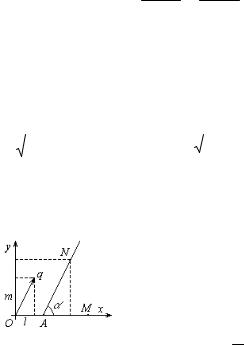
x x1 |
|
y y1 |
(****) |
|
l |
m |
|||
|
|
Это уравнение и называют каноническим уравнением прямой линии.
Отсюда легко найти уравнение прямой, проходящей через две точки М1(х1, у1) и М2(х2, у2). Очевидно, направляющий вектор такой прямой есть
q {x2 x1,y2 y1} {l ;m }
Уравнение, очевидно, есть:
x x1 |
|
y y1 |
||||
|
|
|||||
x |
2 |
x |
|
y |
2 |
y |
|
1 |
|
|
1 |
||
Параметрическое уравнение прямой
Из уравнения (****) можно получить параметрическое уравнение прямой. Действительно, из этого уравнения можно записать:
x x1 y y1 t l m
х - х1 = l t ; y - y1 = m t , или
x x1 lt
y y1 mt
Эту систему легко наглядно представить. Если считать t временем, то координаты х у есть координаты точки, двигающейся по линии с направляющим вектором q {l,m} и имеющей
|
|
|
|
|
1 |
|
|
|
|||
скорость u |
(x x |
)2 (y y |
)2 |
|
l2 m2 . |
||||||
|
t |
|
|||||||||
|
1 |
1 |
|
|
|
|
|
|
|||
Прямая с угловым коэффициентом
Введем понятие угла наклона прямой к оси Ох.
NAM назовем углом наклона прямой к оси Ох. Тангенс угла наклона назовем угловым коэффициентом этой прямой.
k = tg
Из канонического уравнения прямой линии получим:
m
y y1 l (x x1) k(x x1) или y kx b, где b y1 kx1
:
k = tg = m/l
Число b представляет собой величину отрезка, отсекаемого на оси Оу этой прямой.
Угол между двумя прямыми
а). Пусть даны две прямые: A1 x + B1 y + C1 = 0 и A2 x + B2 y + C2 = 0
Т.к. нормальным вектором для первой прямой является вектор n1 {A1,B1}, а для второй n2 {A2 ,B2}, то задача сводится к определению угла между векторами n1 и n2 . Выполним
скалярное |
произведение |
двух |
векторов: |
n1 n2 |
|
|
n1 |
|
|
|
n2 |
|
cos |
получим |
|
|
|
|
cos |
|
|
|
|
A1 A2 B1B2 |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
A |
2 A 2 |
B |
2 B 2 |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||
|
1 |
2 |
|
1 |
2 |
|
|
|
|
|
|
|
||||||||||
|
Условие параллельности двух прямых, очевидно эквивалентно условию коллинеарности n1 |
|||||||||||||||||||||
и n : |
A1 |
|
|
B1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
B |
|
|
|
|
|
|
|
|
|
|
|
||||||||
2 |
A |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Условие перпендикулярности – равенство нулю скалярного произведения |
A1A2 + |
||||||||||||||||||||
B1B2=0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
б). Если две прямые заданы своими каноническими уравнениями |
|
||||||||||||||||||||
|
|
|
x x1 |
|
y y1 |
|
и |
x x2 |
|
y y2 |
, то поскольку направляющие векторы этих прямых есть |
|||||||||||
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
l |
|
m |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
l |
2 |
|
|
|
m |
|
|||||
|
1 |
|
1 |
|
|
|
|
|
|
2 |
|
|
||||||||||
q1 {l1,m1} и q2 {l2 ,m2}, то аналогично предыдущему имеем:
|
|
|
mm l l |
|
|
|
|
|
|
|||
cos |
|
|
1 |
2 |
1 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l 2 |
l |
2 |
|
m 2 m |
2 |
|
|
|
||||
|
|
|
|
|
|
|||||||
1 |
2 |
|
1 |
|
2 |
|
|
|
||||
Условие паралельности - |
l1 |
|
m1 |
|||||||||
|
m |
|||||||||||
|
|
|
|
|
|
|
l |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
||||
Условие перпендикулярности - l1l2 = m1m2.
в). Если две прямые L1 и L2 заданы уравнениями с угловыми коэффициентами:
y= k1 x + b1 и y = k2 x + b2
Из геометрических соображений ясно, что = 2 - 1
tg tg( |
|
|
) |
tg 2 tg 1 |
|
k1 k2 |
|
1 tg 1tg 2 |
1 k1k2 |
||||
|
2 |
1 |
|
|
Условие паралельности - = 0, tg = 0, k1 = k2;
Условие перпендикулярности – его можно получить из условия tg , или 1+ k1k2=0,
1
откуда k1 k2 .
Нормированное уравнение прямой
Поставим задачу: выразить уравнение прямой L через два параметра: 1) длину отрезка OP, где n - единичный вектор нормали OP к прямой 2) угол между вектором nи осью Ох.
Очевидно, n cos ;cos(900 ) {cos ,sin }.
Точка М(х, у) лежит на прямой L тогда и только тогда, когда проекция
OM на ось, определяемую вектором n, равна OP P - длине отрезка OP, обозначенной за Р.
прn OM P
Если n единичный вектор, то в силу определения скалярного произведения, имеем:

n OM n прn OM xcos ysin
Т.е. точка М(х, у) лежит на прямой L тогда и только тогда, когда координаты этой точки удовлетворяют уравнению: xcos ysin p 0.
Это уравнение называется нормированным уравнением прямой.
Как привести уравнение Ax + B y + C = 0 к нормированному виду? Так, как уравнения Ax + B y + C = 0 и xcos ysin p 0 должны определять одну и туже прямую, то должно быть:
1 |
A |
|
B |
|
c |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
, или At cos ; |
Bt sin ; |
ct p. |
|
|
|
|||||
t |
cos |
sin |
p |
|
|
|
||||||||||||
|
|
Возведем |
в |
квадрат |
|
и |
складывая |
первые |
два |
равенства, |
получим |
|||||||
t2 (A2 B2 ) 1; |
|
t |
1 |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
 A2 B2
A2 B2
Знак нужно взять из третьего равенства ct p: поскольку р – расстояние, которое всегда положительно, то знак у t нужно брать противоположным знаку с.
Множитель t |
|
1 |
|
взятый со знаком, противоположным знаку слагаемого с, |
|
|
|
||
|
||||
|
|
A2 B2 |
||
называется нормирующим множителем.
Введем теперь фундаментальное понятие тклонения произвольной точки М от прямой L.
Пусть число d означает расстояние от точки М до прямой L. Назовем отклонением точки М от прямой L число +d, если точка М и начало координат О лежат по разные стороны от прямой L, и число –d в случае, когда М и О лежат по одну сторону от L.
Если же начало координат лежит на прямой L, то отклонение +d положим, когда М лежит по ту сторону от L, куда направлен нормальный вектор n , и –d в противном случае.
Запишем без доказательства, что левая часть нормированного уравнения прямой равна отклонению точки М с координатами (x,y) от прямой, определяемой этим нормированным уравнением. Это дает возможность легко определить расстояние от точки до прямой. Для этого достаточно нормировать уравнение прямой и подставить в него координаты точки (x,y):
d x*cos y*sin p
Уравнение прямой линии в полярных координатах
Из рисунка видно, что:

cos( ) op P Отсюда |
P/cos( ) |
P
или
acos bsin
Лекция 7.
Линии второго порядка
Линии второго порядка это эллипс, гипербола, парабола. Эти кривые представляют собой так называемые конические сечения. Это сечения конуса плоскостью. В зависимости от того, как проходит плоскость получается либо эллипс, либо парабола, либо гипербола. В механике линии второго порядка определяют траектории движения теля в поле центрального тяготения. Так, материальная точка (спутник) движется в поле тяготения Земли по эллипсу. Если его скорость равна второй космической, то по
параболе, а если превысит вторую космическую – то по гиперболе.
Общее уравнение кривой второго порядка – это полином второй степени:
a11 x2 + 2 a12 x y + a22 y2 + 2 a13 x + 2 a23 y + a33 = 0
В математике доказывается (мы этим займемся через несколько лекций), что путем преобразований координат – поворотов осей и переносов осей можно всегда данное уравнение привести к виду:
a11 x2 + a22 y2 = a33 или y2= 2px
Такой вид уравнения кривой второго порядка называется каноническим.
Более того, доказывается также, что этими тремя линиями ( эллипс, парабола, гипербола)
исчерпываются все линии второго порядка.
Рассмотрим в отдельности каждую кривую.
Каноническое уравнение эллипса. Эллипс получается, если плоскость пересекает все образующие конуса.
Эллипсом называется геометрическое место точек плоскости, для которых сумма расстояний до двух фиксированных точек F1 и F2 этой плоскости, называемых фокусами, есть величина постоянная. Очевидно, при совпадении точек
F1 и F2 эллипс представляет собой окружность.
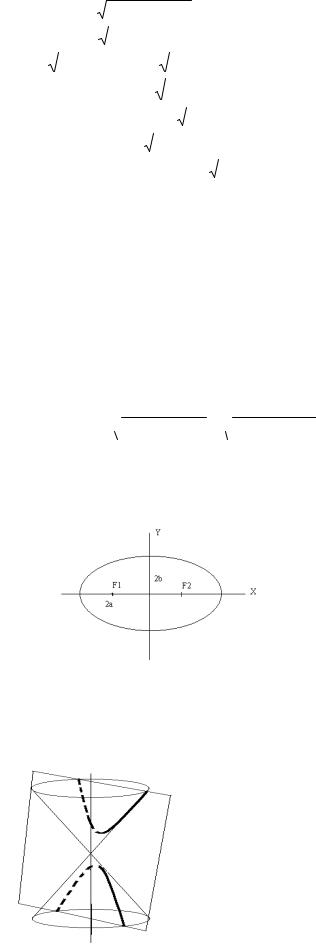
Выведем каноническое уравнение эллипса: выберем начало координат в середине отрезка
F1F2. Обозначим длину отрезка F1F2=2с, а расстояние, о котором мы говорили в определении эллипса – через 2а.
F M |
(x c)2 |
y2 |
|
|
|
|
|
|
|||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F2 M |
(x c)2 y2 |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(x c)2 |
y2 |
|
|
|
(x c)2 |
y2 2a_ _ (*)_ Возводим_ _ в_ _ квадрат: |
||||||||
|
|
|
|
|
(x c)2 y2 4a2 |
||||||||||
(x c)2 y2 2 |
|
(x c)2 y2 (x c)2 y2 |
|||||||||||||
2x2 2c2 2 y2 2 |
|
|
|
4a2 |
|||||||||||
(x c)2 (x c)2 y2 [(x c)2 (x c)2 ] y4 |
|||||||||||||||
x2 y2 c2 |
|
|
|
2a 2 |
|||||||||||
|
(x 2 c2 )2 y2 (x 2 2xc c2 x2 2xc c2 ) y 4 |
||||||||||||||
(x2 c2 ) (y2 |
2a2 |
|
|
|
|||||||||||
) |
(x2 c2 )2 2y 2 (x2 c2 ) y 4 _ _ Снова_ _ возводим_ в_ 2 |
||||||||||||||
(x2 c2 )2 2(x2 c2 )( y2 2a2 ) (y 2 2a2 )2 |
(x2 c2 )2 2 y2 (x2 c2 ) y4 |
||||||||||
4x2 c2 2(x2 y2 2x2 a 2 c2 y 2 2a2 c2 ) y4 4y 2 a2 4a4 |
2 y2 x2 2y2 c2 y4 |
||||||||||
4x2 c2 4x2 a 2 4a2 c2 4y 2 a2 4a4 0 |
|
|
|
||||||||
x2 (c2 a2 ) y 2 a2 a 2 (a2 c2 ) 0 |
|
|
|
||||||||
x2 |
(c2 a2 ) y2 |
c2 a2 |
|
|
|
|
|
||||
a2 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
y2 |
|
|
x 2 |
|
y 2 |
|
|
|
|
|
|
|
1 |
|
|
|
|
1 _ где b2 |
a 2 c2 |
|
|
a2 |
c2 a2 |
|
a 2 |
b2 |
|
||||||
|
|
|
|
|
|
|
|
||||
Лучше проделать следующие преобразования: умножим правую и левую части (*) на
разность радикалов
4xc 2a(
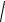 (x c)2 y2
(x c)2 y2 
 (x c)2 y2 ) , сложим снова с (*) и возведем в квадрат
(x c)2 y2 ) , сложим снова с (*) и возведем в квадрат
4((x c)2 y2 ) 4a2 8xc 4x2c2 / a2 _;__ x2 (a2 c2 ) / a2 y2 a2 c2
Отсюда x2 / a2 y2 / b2 1
Величины a и b называются большой и малой полуосями соответственно. Строим эллипс:
Каноническое уравнение гиперболы. Гипербола получается, когда плоскость пересекают образующие обеих полостей конуса.
Гиперболой называется геометрическое место точек плоскости, для которых абсолютная величина разности расстояний до двух фиксированных точек F1 и F2 этой плоскости, называемых
фокусами, есть величина постоянная.
Выберем опять оси координат и начало координат посередине отрезка F1F2. Расстояние F1F2 равно 2с. А разность расстояний обозначим через 2а.

Аналогично предыдущему выводу уравнения эллмпса, имеем:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(x c)2 y2 (x c)2 y2 |
2a |
||
|
|
|
|
|
Преобразуем, как и ранее к виду: |
|||
x2 |
|
y2 |
b2 c2 a2 |
|
||||
|
|
|
1 |
|
||||
a2 |
b2 |
|
||||||
Величины a и b называются действительной и мнимой полуосями гиперболы соответственно. Строим гиперболу:
Сопряженная гипербола – ее ветви будут направлены вверх и вниз. Асимптоты гиперболы очевидно определяются уравнениями:
b b
y |
|
*x__и__ y |
|
* x 2а и 2в – |
|
|
a a
действительная и мнимая оси гиперболы соответственно.
Каноническое уравнение параболы. Парабола получается, когда плоскость, пересекающая конус, параллельна одной из образующих. В механике космического полета существует так называемая параболическая скорость. Иначе еще она называется второй космической скоростью.
Тело, имеющее вторую космическую скорость, движется по параболе, а если скорость больше – то по гиперболе.
Параболой называется геометрическое место точек плоскости, для которых расстояние до некоторой фиксированной точки F этой плоскости равно расстоянию до некоторой фиксированной прямой. Точка F называется фркусом параболы, а фиксированная прямая – директрисой параболы.
Для вывода уравнения построим:
Согласно определению:
r d |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
d |
p |
x |
||
r |
|
|
(x |
p |
)2 y2 |
||||||||||
2 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
||||
(x |
p |
)2 y2 ( |
|
p |
)2 xp x2 |
||||||||||
|
|
|
|||||||||||||
|
2 |
|
2 |
|
|
|
|
|
|
||||||
x2 xp y2 ( |
p |
)2 |
( |
p |
)2 xp x2 |
||||||||||
|
|
||||||||||||||
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|||
y2 |
2px |
|
|
|
|
|
|
|
|
|
|
|
|||
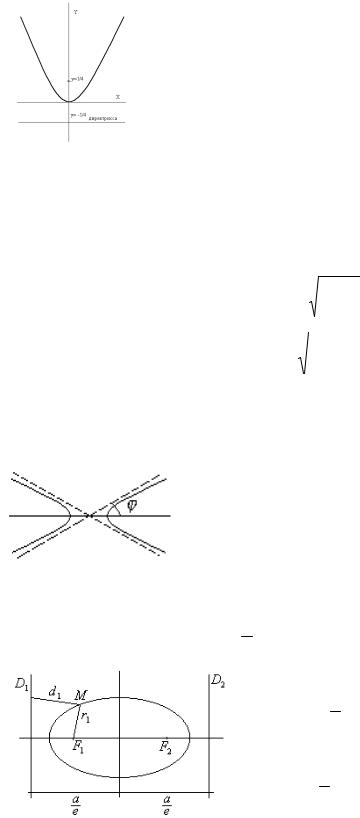
Это и есть каноническое уравнение параболы. Параметр р называеся параметром параболы.
К примеру, парабола y = x2: p=1/2
Фокус – это точка F ( 0, 1/4), директриса y = - 1/4
Оказывается, директрису можно определить и для эллипса и для
параболы. Заметим, что для параболы директрису можно определить и так:
отношение расстояний от точки параболы до фокуса и до директрисы есть величина постоянная, равная единице. Для эллипса и гиперболы можно также ввести прямую, для которой отношение расстояний от некоторой точки эллипса или гиперболы до фокуса и до прямой, называемой тоже
директрисой, есть величина постоянная.
Для выяснения этого свойства введем определение: эксцентриситетом эллипса (гиперболы)
называется величина е, равная e=c/a.
Если обратиться к уравнениям эллипса и гиперболы, то можно получить для е выражение:
b2
e |
1 |
|
|
|
|
- эллипс |
|
a2 |
|
||||||
e |
1 |
b2 |
|
- гипербола |
|||
a2 |
|
|
|||||
e < 1 для эллипса
e = 0 для окружности e > 1 для гиперболы
Заметим, что величина эксцентриситета для эллипса характеризует его вытянутость, а для гиперболы – величину угла раствора ветвей гиперболы. Чем больше эксцентриситет гиперболы,
тем больше угол раствора ветвей .
Определение: директрисой D1 эллипса, отвечающей фокусу F1
является прямая, расположенная в той же полуплоскости, что и фокус F1 , перпендикулярно
a
большой оси эллипса на расстоянии от его центра. e
Уравнение директрисы D1:
a
x
e
Уравнение директрисы D2:
a
x
e
Теперь докажем теорему: отношение расстояния r1 от

точки эллипса M(x,y) до фокуса F1 к расстоянию d1 от этой точки эллипса до директрисы D1 есть
величина постоянная, равная эксцентриситету эллипса: r1 e. d1
Действительно:
r |
|
|
|
|
(x c)2 b2 x2 |
b2 |
|
(x c)2 a2 c2 x2 |
b2 |
|
||||||||||||||||||||||
(x c)2 y2 |
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
a2 |
|
|
|
|
|
|
|
|
|
|
|
|
a2 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
x2(1 |
b2 |
) 2xc c2 |
a2 |
c2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Нормированное |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
a2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
x2(1 |
a2 c2 |
) 2xc a2 |
x2 |
c2 |
2xc a2 |
a x |
c |
|
a ex |
|
||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
a2 |
|
|
|
|
a2 |
|
|
|
|
|
|
|
|
|
a |
|
|||||||||||||
уравнение директрисы есть: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
xcos ysin p 0 |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
x y 0 |
a |
0 |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
e |
|
|||||||||||||||||||||
Расстояние d1, очевидно есть (подставляем координаты точки М в нормированное |
||||||||||||||||||||||||||||||||
уравнение): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
d1 |
|
x |
a |
|
|
|
xe a |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
e |
|
|
e |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
отношение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r1 |
|
a ex |
e e |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d1 |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a ex |
|
||||||||||||||||
Теорема доказана.
Определим директрису для гиперболы. Директрисой D1 гиперболы, отвечающей фокусу F1
называется прямая, расположенная в полуплоскости, где расположен фокус F1, перпендикулярно
|
a |
|
действительной оси гиперболы на расстоянии |
|
от центра. |
|
||
|
e |
|
Можно доказать, аналогично эллипсу, теорему: отношение |
||
расстояние r1 |
некоторой точки гиперболы до ее фокуса F1 к |
|
расстоянию до директрисы d1 равно r1 e. d1
Эти свойства эллипса и гиперболы позволяют дать новое определение этих кривых. Действительно следующее утверждение: геометрическое место точек М на плоскости, для которых отношение е расстояния r до точки F к расстоянию d до некоторой прямой D есть величина постоянная, представляет собой эллипс, если e < 1 или параболу, если e = 1,
