Lineynaya algebra i analitich_geom / Ivleva_i_kurs_lekciy_po_lineynoy_algebre_i_analiticheskoy_ge

aj bi ci bj ... cj

а это и означает линейную комбинацию строк.

Достаточность. Пусть одна из строк является линейной комбинацией других, т.е.

A B C

последнее равенство устанавливает линейную зависимость строк.

Ранг матрицы

Запишем определение. Минором k-того порядка матрицы А называется определитель k-того порядка с элементами, лежащими на пересечении любых k строк и любых k столбцов.

Предположим, что хотя бы один элемент матрицы А отличен от 0. Тогда найдётся такое целое положительное число r, что будут выполнены два условия:

1)у матрицы А имеется минор r-того порядка, отличный от 0;

2)всякий минор (r+1)-го порядка и более (если такие есть), равен нулю.

Число r, удовлетворяющее двум требованиям, назовём рангом матрицы. А минор r-того порядка, который отличен от нуля, назовём базисным минором. Строки и столбцы, из которых состоит базисный минор, называются базисными строками и базисными столбцами.

Теорема о базисном миноре (без доказательства).

Базисные строки (или столбцы) линейно независимы. Любая строка (столбец) матрицы А является линейной комбинацией базисных строк (столбцов).

Итак, если у матрицы все миноры порядка k>r равны нулю, а среди миноров r-того порядка хотя бы один не равен нулю, то число r называется рангом матрицы.

Для того, чтобы вычислить ранг матрицы, необходимо, очевидно, вычислить все её миноры и среди них найти минор наибольшего порядка, не равный нулю. Отсюда, кстати следует, что ранг невырожденной матрицы равен порядку матрицы.

Существует, однако, более простое правило вычисления ранга матрицы. Прежде чем к нему обратиться, условимся считать элементарными следующие преобразования матрицы:

1) умножение всех элементов строки на число 0;

2)сложение элементов одной строки с элементами другой строки, умноженными на некоторое число ;

3)перемена местами строк матрицы.

Теорема без доказательства: элементарные преобразования матрицы не меняют её ранга.

Поясним всё сказанное простым примером:

Если посчитать её определитель, то можем убедиться, что она вырождена, её det=0.

или, условно нарисуем:

Обратим внимание на коэффициент br 1 . Может случиться, что это будет 0. А может и нет.

Тогда 0 br 1 0, что невозможно. Значит решений нет, т.е. система несовместна. Поэтому на

практике, сразу же после появления соотношения вида 0 h 0 можно говорить, что система не имеет решения.

Если br 1 0, то, покажем, что система имеет решение. Поскольку arr 0, то из последнего уравнения можно найти

предыдущего уравнения можно найти

из этих соотношений следует, что xr+1,...,xn могут принимать произвольные значения. Эти неизвестные называются свободными, а x1,...xr - называются основными или главными. Любая совокупность свободных неизвестных и соответствующих им основных будет решением системы. Таким образом, мы доказали теорему:

Теорема Кронекера-Капелли: для того, чтобы система уравнений (**) была совместной, необходимо и достаточно, чтобы ранг матрицы этой системы и ранг расширенной матрицы были равны.Далее, предположим мы выяснили, что система уравнений совместна. Тогда возможны два случая:

1) ранг матрицы равен количеству неизвестных R=N. Это возможно, кстати, при m n.В этом случае все неизвестные главные и они равны из (****):

x1 1 x2 2 ... xn n

Это означает, что система имеет единственное решение. Система определённая.

2) r<n. В этом случае имеются свободные неизвестные, которые можно задавать произвольно. Значит система имеет бесконечное множество решений, т.е. система неопределённая!

Для того, чтобы система однородных уравнений имела решения, отличные от нулевого, необходимо и достаточно, чтобы ранг матрицы системы был меньше числа неизвестных. Другими словами, если число уравнений равно числу неизвестных, то система имеет ненулевое решение тогда и только тогда, когда detA=0.

Очевидны следующие свойства ненулевого решения:

Решения X1,X2,…,Xn-r называются фундаментальной системой решений однородной системы. Общее решение системы X является линейной комбинацией фундаментальной системой решений

X=c1X1+c2X2+...+cn-rXn-r.

Пример:

9x1 21x2 15x3 5x4 012x1 28x2 20x3 7x4 0

Теперь сформулируем понятие равенства двух векторов: два вектора называются равными,

если они коллинеарны, имеют одинаковую длину и направление. Два нулевых вектора считаются равными.

Из определения равенства векторов следует, что мы не различаем двух равных векторов,

имеющих разные точки приложения. Иными словами, точка приложения вектора a может быть произвольной. В соответствии с этим векторы в геометрии называются свободными.

Определим линейные операции над векторами.

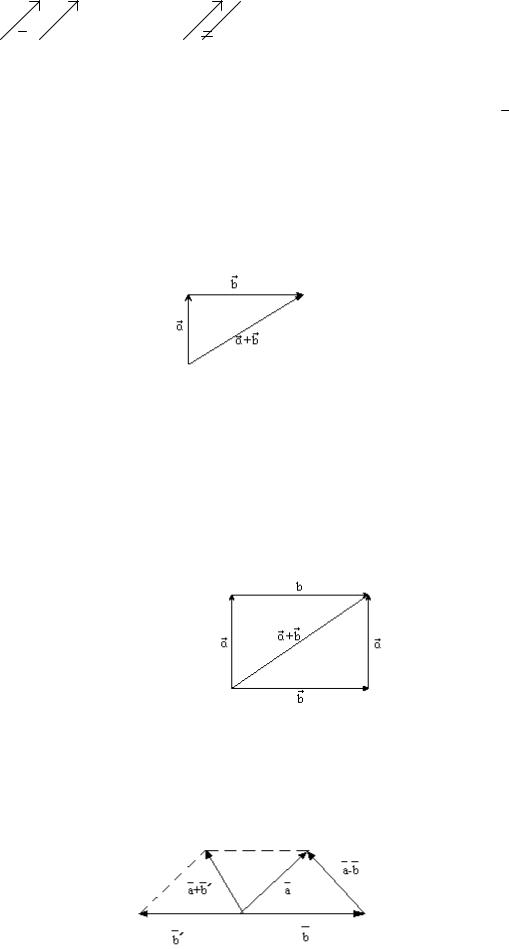
Сложение. Суммой a b двух векторов a и b называется вектор, идущий из начала вектора a в конец вектора b при условии, что начало b приложено к концу вектора a .

Геометрически это можно изобразить правилом треугольника:

Правило сложения векторов обладает теми же четырьмя свойствами, что и правило сложения вещественных чисел:

1.a b b a (переместительное свойство).

2.(a b) c a (b c) (сочетательное свойство).

3.Существует нулевой вектор, такой, что a 0 a .

4.Для каждого a существует такой a что a a 0.

Эти свойства доказываются геометрическими построениями. К примеру свойство 1:

Эти свойства позволяют оперировать с векторами так же как и с вещественными числами.

Определим разность векторов a b как сумму a b , где b - противоположный вектор