Lineynaya algebra i analitich_geom / Ivleva_i_kurs_lekciy_po_lineynoy_algebre_i_analiticheskoy_ge

Лекция 11.

Линейные пространства

В дальнейшем мы будем говорить о множестве некоторых элементов произвольной природы, для которых определены некоторые операции, подчиняющиеся определенным ограничениям, называемым аксиомами.

Такие множества называются пространствами, а их элементы – точками или векторами. Однако подчеркнем, что «векторы» таких абстрактных пространств, как правило, ничего общего не имеют с векторами, изучаемыми в геометрии. Элементами пространства могут быть функции, матрицы, системы чисел и т.д., а в частном случае и обычные векторы.

В дальнейшем из всех пространств мы выделим для изучения так называемые линейные пространства, обладающие целым рядом общих свойств, которые и будут установлены далее.

Прежде всего, определим числовое поле. Числовым полем К называется множество чисел ,, , ... , если для любых и из множества К числа + , , - , / также принадлежат этому множеству. Т. е. Множество чисел, замкнутых относительно арифметических операций. Например, множество чисел вида a + b 2, где a и b любые рациональные числа образуют поле, а если a и b – целые числа, то поля не образуются. Действительно, рассмотрим, например, операцию / : = a + b 2 = c + d 2

не целые!

Теперь, наконец, определим линейное пространство. Линейным или афинным пространством над числовым полем K называется множество R элементов, которые будем называть векторами и обозначать x; y; z, ... , если:

1). Указан закон, согласно которому любой паре векторов x R (значок означает, что х – элемент множества R) и y R однозначно ставится в соответствие вектор z R, также принадлежащий множеству R. Вектор z называется суммой векторов x и y и обозначается z = x + y; 2). Указан закон, согласно которому каждому числу из поля K и любому вектору x R однозначно ставится в соответствие вектор z R. Вектор z называется произведением вектора x на

число и обозначается z = x = x ;

3). Введение в этих двух пунктах операции сложения и умножения удовлетворяют следующим восьми аксиомам:

0 R | x R ( x + 0 = x )

40. Для каждого элемента x существует противоположный элемент x’ такой, что x + x’ = 0. Вектор x’ называется противоположным вектору x и обозначается –x или: x R (-x) R | x + ( - x) = 0.

50. 1 * x = x для каждого элемента x: x R (1 * x = x) – это существование единичного элемента.

60. ( x ) = ( ) x – сочетательное свойство относительно числового множителя.

70. ( + ) x = x + x – распределительное относительно суммы числовых сомножителей. 80. ( x + y ) = x + y – распределительное относительно суммы элементов.

Следует подчеркнуть, что в определении линейного пространства мы абстрагируемся не только от природы изучаемых объектов, но и от конкретного вида правил образования суммы элементов и произведения x.

Примеры линейных пространств:

1.множество всех свободных векторов. Операции сложения и умножения векторов

определены в аналитической геометрии. Элементарно можно проверить справедливость всех аксиом 10- 80. Т.е. множество всех свободных векторов является линейным пространством. Будем обозначать его V3. Аналогичные линейные пространства на плоскости и на прямой будем обозначать V2 иV1 соответственно.

2.Множество An, элементами которого служат упорядоченные совокупности n произвольных вещественных чисел (x1, x2, ... , xn). Элементы этого множества мы будем обозначать

x= (x1, x2, ... , xn) и называть числа x1, ... , xn – координатами элемента x. В анализе множество An обычно называют n – мерным координатным пространством. В алгебраической трактовке – это совокупность всевозможных строк, каждая из которых содержит n вещественных чисел. Если определить операцию сложения и умножения как:

(x1 x2 ... xn) + (y1 y2 ... yn) = (x1+ y1; x2+ y2; ... ; xn+ yn)(x1 x2 ... xn) = ( x1 x2 ... xn)

то можно убедиться в справедливости всех восьми аксиом.

3.Множество всех многочленов степени, не превосходящей n. В этом пространстве вектор

xимеет вид:

x= A0 tn + A1 tn-1 + ... + An

Обратим внимание, что множество всех многочленов степени строго n не является линейным пространством. Действительно, если x = A0 tn + A1 tn-1 + ... + An , а у есть y = -A0 tn + A1 tn-1 + ... +

An , то x + y = 2 A1 tn-1 + ... + 2 An – многочлен, степени ниже n!

4. Множество С [a, b] всех функций x = x (t), определенных и непрерывных на сегменте a t b. Операции сложения и умножения на число определены обычными правилами математического анализа. Легко видеть справедливость аксиом 10- 80.

Будем называть вещественным линейным пространством пространство, определенное над вещественным полем числом K. При более широком подходе можно брать числа из комплексного поля. В таком случае придем к понятию комплексного линейного пространства.

Некоторые свойства произвольных линейных пространств.

Запишем без доказательства два утверждения:

1). В произвольном линейном пространстве существует единственный нулевой элемент и для каждого элемента x существует единственный противоположный.

2). В произвольном линейном пространстве: а) нулевой элемент 0 равен произведению произвольного элемента x на вещественное число 0; б) для каждого элемента x противоположный элемент равен произведению этого элемента x на вещественное число –1.

Пусть некоторое множество L является линейным пространством. Всякое подмножество L1 пространства L, элементы которого в свою очередь образуют линейное пространство, (с теми же операциями сложения и умножения) называется подпространством пространства L. Очевидно, что единственный нулевой вектор 0 L и само пространство L являются наименьшим и наибольшим подпространствами линейного пространства L.

Примеры подпространства: в пространстве векторов V3 векторы, параллельные некоторой плоскости образуют подпространство V2.

Определение линейной оболочкой векторов x1 x2 ... xm – некоторой системы векторов пространства L - называется совокупность всех линейных комбинаций этих векторов, т.е. множество элементов вида

1 x1 + 2 x2 + ...+ m xm

где 1 2 ... m – произвольные действительные числа. Линейную оболочку будем обозначать L (x1 x2 ... xm).

Иногда говорят, что линейная оболочка – это подпространство, натянутое на данную систему векторов.

Размерность и базис линейного пространства.

В пространстве V3 каждый вектор можно единственным образом разложить по трем некомпланарным векторам, которые называются базисом пространства V3. Рассмотрим вопрос о построении базиса в произвольно пространстве R. Для этого повторим некоторые важные понятия.

Линейная зависимость векторов. Если x1 x2 … xn – векторы линейного пространства R, а 1 2 …n – произвольные числа из поля K, то выражение

1 x1 + 2 x2 +…+ n xn

называется линейной комбинацией векторов x1 x2 … xn, а числа 1 2 … n называются коэффициентами этой линейной комбинации. Если линейная комбинация векторов обращается в нуль тогда и только тогда, когда все i = 0, то вектора являются линейно независимыми. В противном случае, когда

1 x1 + 2 x2 +…+ n xn = 0

при условии, что хотя бы один i = 0, вектора называются линейно зависимыми.

Вспомним, что мы доказывали, что любая совокупность векторов x1 x2 … xn, содержащая нулевой вектор, является линейно зависимой. Точно также система векторов x1 x2 … xn, содержащая совокупность линейно зависимых векторов, линейно зависима.

Наконец, докажем теорему, что векторы x1 x2 … xn линейно зависимы тогда и только тогда, когда хотя бы один из них можно представить как линейную комбинацию оставшихся.

Другими словами, нужно доказать необходимость и достаточность. Докажем необходимость. Пусть x1 x2 … xn линейно независимы. Тогда:

x1 + x2 +…+ xn = 0

причем хотя бы одно из чисел , , …, 0. Положим, что 0. Тогда

а это по определению означает линейную комбинацию. Достаточность: пусть x1 является линейной комбинацией оставшихся, т.е. равенство (*) выполнено. Тогда перепишем его в виде:

( 1)x1 x2 ... xn 0

Поскольку из чисел (-1), , … , одно не равно нулю (-1), то это означает линейную зависимость векторов x1 x2 … xn.

а) Размерность линейного пространства.

Если в линейном пространстве R существует n линейно независимых векторов, а любые n + 1 векторов этого пространства линейно зависимы, то линейное пространство называется n – мерным. Число n называется размерностью пространства. Символ размерности - dim R.

Например, пространства V3 и V2 соответственно трехмерные и двухмерные. Существуют бесконечномерные линейные пространства. Пример такого пространства – это векторы x и y из пространства С [a, b]. Их сумма и произведение имеют вид:

В линейной алгебре изучаются только конечномерные пространства.

б) Базис линейного пространства.

Система { e } из n линейно – независимых векторов n – мерного пространства e1 e2...en ,

заданных в определенном порядке, называется базисом этого пространства.

Теорема: любой вектор х n – мерного пространства и при том единственным образом, можно разложить по базису этого пространства e1 e2...en .

Действительно, векторы x e1 e2...en линейно зависимы т.к. их число равно n + 1, а по

определению базиса n – мерного пространства n + 1 векторов линейно зависимы. Тогда составим выражение:

0 x 1 e1 2 e2 ... n en 0

где хотя бы одно i будетотлично от 0. 0 0, т.к. иначе окажется, что базисные вектора линейно зависимы. Тогда:

т.е. можно представить x как линейную комбинацию векторов базисных. Причем, разложение это единственно. Запишем разложение в виде:

xx1 e1 x2 e2 ... xn en

иназовем числа x1 x2 … xn координатам вектора x в базисе e1 e2...en . Будем писать

x{x1 x2...xn}.

Действия над векторами в координатной форме.

Если в линейном n – мерном пространстве заданы два вектора x x1 e1 x2 e2 ... xn en ; y y1 e1 y2 e2 ... yn en то на основании аксиом, которым удовлетворяют операции сложения и умножения, будем иметь:

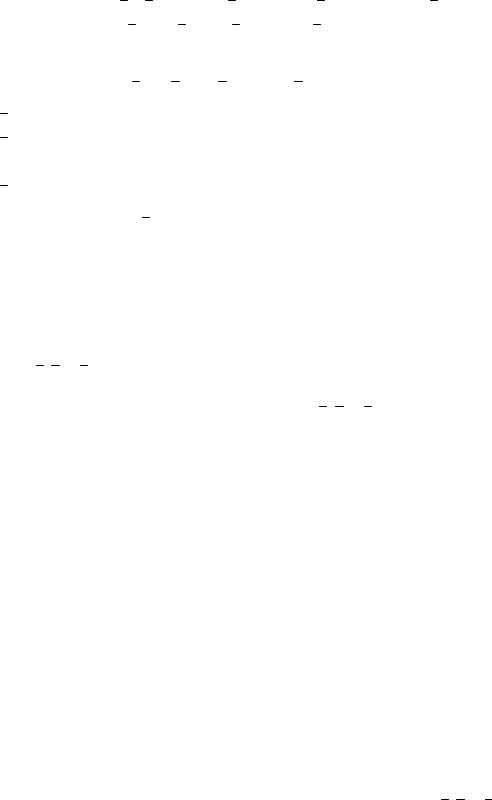
x y (x1 y1)e1 (x2 y2 )e2 ... (xn yn )enx x1 e1 x2 e2 ... xn en

Рассмотрим линейную комбинацию векторов:

Если координаты вектора y есть {y1 y2...yn}, то имеем систему уравнений:

Рассмотрим матрицу этой системы. Ее столбцы – координаты векторов x1 x2 … xn. Если предположить, что в равенстве (*) вектор у равен 0, то мы будем иметь линейную зависимость векторов x1 x2...xm . Чтобы система (**) имела ненулевое решение ( когда yi = 0, i = 1, … , n)

ненулевое решение! – необходимо (из предыдущего материала) чтобы ранг матрицы был меньше числа неизвестных m. Или, с другой стороны, вектора x1 x2...xm линейно независимы, когда ранг матрицы (**) равен числу векторов.

Максимальное число линейно независимых векторов линейного пространства – есть размерность пространства – и это же число является рангом некоторой системы векторов (*). Обратимся к примеру: найти размерность и базис пространства, являющегося линейой оболочки векторов: x1 = ( 0, 2, -1 ) x2 = ( 3, 7, 1 ) x3 = ( 2, 0, 3 ) x4 = ( 5, 1, 8 ).

Базисом могут служить три линейно независимых вектора. А это векторы x1 x3 x4, поскольку x2 – их линейная комбинация.

На основе вышесказанного можно сделать вывод: ранг системы векторов x1 x2...xm равен рангу матрицы из координат этих векторов в некотором базисе.

Замена базиса

Рассмотрим линейное преобразование координат некоторого вектора при смене базиса. Предположим, что мы имеем два базиса произвольного n – мерного пространства e1 e2...en и e1 e2...en . Очевидно, координаты векторов одного базиса e1 e2...en можно выразить через другой базис:

В матричном виде:

где матрица А – это матрица, связывающая новый базис еi’ со старым ei.

Рассмотрим некоторый вектор

x x1e1 x2e2 ... x1nen x1e1 x2e2 ... x1nen

Подставим здесь вместо e1 e2...en их выражения из (*):

x1e1 x2e2 xnen x1( 11e1 12e2 1nen)

x2( 21e1 22e2 2nen) xn1( n1e1 n2e2 nnen)

Приравнивая здесь коэффициенты при одинаковых векторах ei , приходим к системе уравнений:

x1 11x1 21x2 n1xn x2 12x1 22x2 n2xn

Матрица АТ, транспонированная к А, называется матрицей перехода от одного базиса к другому. Столбцами этой матрицы являются координаты новых базисных векторов в старом базисе. Очевидно, обратный переход есть: x’=(A –1)Tx

Вывод: если переход от первого базиса ко второму осуществляется с помощью невырожденной матрицы А, то переход от координат произвольного элемента относительно первого базиса к

координатам этого элемента относительно второго базиса осуществляется с помощью транспонированной обратной матрицы.

Пример: в пространстве V3 имеем два базиса:

1)e1 i;e2 j;e3 k;

2)e1 i j k;e2 i j;e3 i;

В заключении рассмотрим пространства решений линейной однородной системы. Если решений множество, то известно, что сумма каких-либо решений тоже является решением и произведение каких-либо решений на число тоже является решением. Аксиомы 10 – 80 тоже выполняются. Т.е. множество решений линейной однородной системы являются линейным пространством. Существует теорема: размерность пространства решений линейной однородной системы уравнений с n неизвестными равна n-r, где r – ранг матрицы системы.

X = Cr+1X1+ Cr+2X2 + … + CnXn-r

Это означает, что решения X1 … Xn-r – линейно независимы и их можно принять за базис пространства решений. Любой базис решений называется фундаментальной системой решений.

Лекция 12.

Евклидовы пространства.

Из курса аналитической геометрии нам знакомо понятие скалярного произведения векторов.

На прошлой лекции мы ввели понятие линейного пространства. Введем теперь в рассмотрение

линейное пространство, для элементов которого каким либо способом определено правило,

ставящее в соответствие двум элементам число, называемое скалярным произведением. Такие

пространства называются евклидовыми линейными пространствами.

Определение евклидового пространства. Линейное пространство R называется евклидовым

пространством, если выполнены два требования:

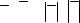
1.Имеется правило, посредством которого любым двум элементам этого пространства x и y ставится в соответствие вещественное число, называемое скалярным произведением этих элементов и обозначается символом (x, y).

2.Указанное правило подчинено следующим четырем аксиомам:

10 (x, y) = (y, x) – переместительное свойство (или симметрия). 20 (x1 + x2, y) = (x1, y) + (x2, y) (распределительное свойство). 30 ( x, y) = (x, y) (для любого вещественного ).

40 (x, x) > 0, если x 0 и (x, x) = 0, если x = 0.

Пример 1. Рассмотрим пространство V3 всех свободных векторов. Скалярное произведение определим, как это сделано было в аналитической геометрии. Все аксиомы 10 - 40 при введенном нами ранее определении скалярного произведения

a b a b cos

будут выполняться. Стало быть, линейное пространство V3 со скалярным произведениям – евклидово пространство.

Пример 2. Рассмотрим бесконечно – мерное пространство C[a, b] всех функций a t b.

Скалярное произведение определим как интеграл от этих функций в пределах от a до b:

b

x(t)y(t)dt

a

Можно проверить справедливость аксиом 10 - 40. Т.е. это бесконечно - мерное евклидово пространство.

Пример 3. Рассмотрим линейное пространство An упорядоченных совокупностей n

вещественных чисел - пространство координат элементов. Положим

x= ( x1 x2 x3 … xn )

y= ( y1 y2 y3 … yn )

тогда введением скалярного произведения в виде

(x, y) = x1y1 + x2y2 + …+ xn yn

можно получить, как не трудно убедиться, евклидово пространство. Определим несколько шире скалярное произведение.

Пример 4. Рассмотрим квадратную матрицу порядка n:

С помощью этой матрицы составим однородный многочлен второго порядка относительно переменных x1, x2, …, xn

n n

aik xi xk i 1 k 1

Такой многочлен называется квадратичной формой, порождаемой квадратной матрицей А (*).

Квадратичная форма называется положительно определенной, если она принимает строго положительные значения для всех значений переменных, одновременно не равных нулю и равна нулю лишь при условии, что x1 = x2 = … = xn = 0. Потребуем, чтобы матрица А удовлетворяла двум условиям:

10 порождала положительно определенную квадратичную форму

20 была симметричной относительно числовой диагонали, т.е. aik = aki для всех i = 1, 2, …, n ; k = 1, 2, …, n. С помощью матрицы, удовлетворяющей двум этим условиям, определим скалярное произведение двух элементов пространства An

Посмотрим на аксиомы 20 и 30 . Они, очевидно, удовлетворяются при совершенной произвольной матрице A. Справедливость 10 вытекает из симметричности матрицы, а 40 – квадратичная форма матрицы А – положительно определенная. Т.о. пространство An со скалярным произведением,

определяемым равенством (**) при условиях 10 и 20 , налагаемых на матрицу А, является евклидовым пространством. Если в качестве матрицы А взять единичную матрицу, то мы получим евклидово пространство, рассмотренное в примере 3, обозначаемое как Еn.

Неравенство Коши-Буняковского

Теорема. Для любых двух элементов х и у произвольного евклидового пространства справедливо неравенство

(x, y)2 (x, x) (y, y),

называемое неравенство Коши – Буняковского.

Доказательство: в силу аксиомы 40 имеем

( x – y, x - y) 0.

В силу аксиом 10 - 30 раскроем это неравенство:

2 (x, x) - 2 (x, y) + (y, y) 0

Этот трехчлен больше или равен нулю. Т.е. квадратное уравнение относительно не имеет действительных корней, а может иметь лишь нулевой корень. Значит его дискриминант равен или меньше нуля:

D = (x, y)2 – (x, x) (y, y) 0

Теорема доказана.

Норма вектора. Нормированное пространство

Определим длину или норму вектора, которую обозначим

x(x,x) ,

здесь учтена аксиома 40 и берется арифметическое значение корня. Из определения нормы вытекает:

1)|x| > 0 при x 0 и |x| = 0 только, если x = 0.

2)| x| = | | |x|

Вектор x, длина которого равна единице, называется нормированным. Очевидно, всякий

ненулевой вектор можно пронормировать, умножив его на число 1 . Полученный x

вектор y x будет нормированным. x

Определим угол между векторами. Углом между векторами назовем угол, косинус которого определяется из соотношения

в силу неравенства Коши – Буняковского |cos | 1, что корректно.

Договоримся считать два вектора евклидового пространства х и у ортогональными, если их скалярное произведение равно нулю. Отсюда следует, что в евклидовом пространстве справедлива теорема Пифагора:

|| x + y ||2 = (x + y, x + y) = (x, x) + 2(x, y) + (y, y) = || x ||2 + || y ||2

Приведем пример условия ортогональности двух векторов x и y в пространстве An