
- •Н.И. Николаева
- •Оглавление
- •Глава 1. Линейная алгебра
- •Матрицы и действия над ними
- •Линейные операции над матрицами
- •Транспонирование и умножение матриц
- •Определители и их свойства
- •Обратная матрица
- •Крамеровские системы уравнений
- •Ранг матрицы. Элементарные преобразования
- •Исследование произвольных систем линейных уравнений
- •Однородные системы линейных уравнений
- •Метод гаусса
- •Глава 2. Векторная алгебра векторы и линейные операции над ними
- •1. Сложение
- •2. Умножение на число
- •Проекция вектора на ось. Координаты вектора
- •Деление отрезка в данном отношении
- •Скалярное произведение векторов
- •Векторное произведение векторов
- •Смешанное произведение веторов
- •Глава 3. Аналитическая геометрия прямая на плоскости. Общее уравнение прямой на плоскости
- •Уравнение прямой с направляющим вектором
- •Уравнение прямой с угловым коэффициентом
- •Угол между прямыми на плоскости
- •Расстояние от точки до прямой на плоскости
- •Кривые второго порядка. Окружность
- •Гипербола
- •Парабола
- •Преобразования координат на плоскости
- •Линейные преобразования на плоскости
- •Произведение линейных преобразований
- •Приведение квадратичной формы к каноническому виду
- •Приведение общего уравнения кривой второго порядка к каноническому виду
- •Плоскость
- •Особые случаи расположения плоскости
- •Уравнение плоскости в отрезках
- •Уравнение плоскости, проходящей через три точки
- •Угол между плоскостями
- •Прямая линия в пространстве
- •Канонические уравнения прямой в пространстве
- •Угол между прямыми в пространстве
- •Приведение общих уравнений прямой в пространстве к каноническому виду
- •Угол между прямой и плоскостью
- •Определение общих точек прямой и плоскости
- •Цилиндрические поверхности
- •Поверхности вращения
- •Библиографический список
Проекция вектора на ось. Координаты вектора
Осью называется направленная прямая.
ОПРЕДЕЛЕНИЕ.
Ортом
оси
![]() называется единичный вектор
называется единичный вектор![]() ,
направление которого совпадает с
направлением оси.
,
направление которого совпадает с
направлением оси.
ОПРЕДЕЛЕНИЕ.
Ортогональной
проекцией
точки М на ось
![]() называется основание М1
перпендикуляра, опущенного из М на
называется основание М1
перпендикуляра, опущенного из М на
![]() .
.
ОПРЕДЕЛЕНИЕ.
Ортогональной
проекцией
вектора
![]() на ось
на ось![]() называетсядлина
отрезка А1В1
этой оси, заключенного между ортогональными
проекциями его начала и конца, взятая
со знаком «+», если направление вектора
называетсядлина
отрезка А1В1
этой оси, заключенного между ортогональными
проекциями его начала и конца, взятая
со знаком «+», если направление вектора
![]() совпадает с направлением оси, и со знаком
«–», если эти направления противоположны
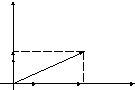
(рис. 8).
совпадает с направлением оси, и со знаком
«–», если эти направления противоположны
(рис. 8).

Рис. 8
![]()
ОПРЕДЕЛЕНИЕ. Углом между вектором и осью называется угол, на который нужно повернуть в положительном направлении ось до совпадения ее направления с направлением вектора (положительным считается поворот против часовой стрелки).
![]() (рис. 8).
(рис. 8).

Очевидно, проекцию вектора на ось можно найти по формуле
![]()
Можно показать, что проекция линейной комбинации векторов равна такой же линейной комбинации их проекций:
![]() .
.
В частности, проекция суммы векторов равна сумме их проекций:
![]() .
.
Рассмотрим
прямоугольную декартову систему
координат ХОY.
Обозначим
![]() – орт оси ОХ,
– орт оси ОХ,![]() – орт осиOY.
Выберем точку
– орт осиOY.
Выберем точку
![]() ,
и пусть
,
и пусть![]() – проекции ее на ОХ иOY,то
есть координаты этой точки (рис. 9).
– проекции ее на ОХ иOY,то
есть координаты этой точки (рис. 9).
|
y A2 A
A1
О
Рис. 9 |
Аналогично
|
Аналогично в
пространственной системе OXYZ
![]() – орты координатных осей) (рис. 10):
– орты координатных осей) (рис. 10):
![]()
– разложение
![]() по ортам координатных осей (единственно
по теореме 2).
по ортам координатных осей (единственно
по теореме 2).
|
A3 z
A
O
A1 x B X
Рис. 10
|
Таким образом,
если задана
прямоугольная декартова система
координат (пдск), то со всяким
пространственным вектором
![]() можно связать три числа
можно связать три числа![]() (или два числа
(или два числа![]() ,
если вектор плоский), которые являются
коэффициентами разложения этого вектора
по ортам координатных осей, а также
являются проекциями этого вектора на
координатные оси.
,
если вектор плоский), которые являются
коэффициентами разложения этого вектора
по ортам координатных осей, а также
являются проекциями этого вектора на
координатные оси.
ОПРЕДЕЛЕНИЕ.
Координатами
вектора
![]() в любойпдск
называются коэффициенты в разложении
этого вектора по ортам координатных
осей.
в любойпдск
называются коэффициенты в разложении
этого вектора по ортам координатных
осей.
Таким образом, можно дать еще одно определение вектора.
ОПРЕДЕЛЕНИЕ. Вектором называется упорядоченная тройка чисел (упорядоченная пара, если вектор плоский).
ПРИМЕР.
Если
![]() ,
то
,
то![]() =(2,3,4)
и наоборот, если
=(2,3,4)
и наоборот, если![]() ,
то
,
то![]()
Так как, с одной стороны, вектор – объект, имеющий длину и направление, а с другой, – упорядоченная тройка чисел, то, зная длину и направление, можно определить его координаты и наоборот. Направление вектора в заданной системе координат характеризуется его направляющими косинусами (рис. 11):
![]() .
.
Пусть
![]()

|
O
X Рис. 11 |
Из этих формул очевидно следует основное свойство направляющих косинусов:
Если
известны длина
|
![]()
|
O y
x Рис. 12 |
Пусть
Тогда
|
![]() (см. свойства
линейных операций над векторами). Таким
образом,
(см. свойства
линейных операций над векторами). Таким
образом,
![]() ,
то естьдля
определения
координат вектора надо из координат
его конца вычесть координаты начала.
,
то естьдля
определения
координат вектора надо из координат
его конца вычесть координаты начала.
ОПРЕДЕЛЕНИЕ. Базисом в пространстве называется любая упорядоченная тройка некомпланарных векторов (рис. 13).
|
Рис. 13 |
Если
ОПРЕДЕЛЕНИЕ. Базис называется прямоугольным декартовым, если базисные векторы взаимно перпендикулярны и длина каждого равна 1.
|
Такой базис принято
обозначать
![]() .
.
Из теоремы 2
следует, что всякий вектор
![]() может быть разложен по базису
может быть разложен по базису![]() ,
то есть представлен в виде:
,
то есть представлен в виде:![]() .
Числа
.
Числа![]() называются координатами
называются координатами![]() в базисе
в базисе![]() .
.
ОПРЕДЕЛЕНИЕ. Базисом на плоскости называется любая упорядоченная пара неколлинеарных векторов.
Если
![]() – базис,
то представление вектора в виде
– базис,
то представление вектора в виде
![]() называется разложением
называется разложением![]() по базису
по базису
![]() и
и
![]() – координаты
– координаты
![]() в этом базисе.
в этом базисе.
ОПРЕДЕЛЕНИЕ. Базисом на прямой называется любой ненулевой вектор этой прямой.

 Y
Y Z
Z Z
Z
 z
z
