Прямая линия в пространстве

Всякая линия в пространстве есть результат пересечения двух поверхностей. В частности прямую линию можно рассматривать как результат пересечения двух плоскостей

и

Если не параллельна, то естьне коллинеарен, то система уравнений

(3.42)

определяет прямую линию в пространстве.

Рис. 48

Уравнения (3.42) называются общими уравнениями прямой в пространстве. Очевидно, одна и та же прямая может быть результатом пересечения разных пар плоскостей (рис. 48), поэтому прямую в пространстве можно задать различными способами. Уравнения (3.42) неудобны в использовании, так как не дают представления о расположении прямой относительно выбранной системы координат.

Поэтому выведем более удобные уравнения, эквивалентные (3.42), то есть из бесконечного множества плоскостей, проходящих через данную прямую, выберем в некотором смысле более заметную пару.

Канонические уравнения прямой в пространстве

Пусть в некоторой пдск задана прямая , проходящая через точкупараллельно ненулевому вектору. Такой вектор называетсянаправляющим вектором этой прямой.

z A M О y x Рис. 49

Для произвольной точки вектор где– некоторый числовой множитель. Кроме того,– радиус-вектор точки,– радиус-вектор точки(рис. 49). Отсюда (3.43)

(3.43) – векторное уравнение прямой в пространстве. Из (3.43) получаем:

(3.44)

(3.44) – параметрические уравнения прямой в пространстве, – параметр.

Выразим из каждого уравнения (3.44) параметр:

.

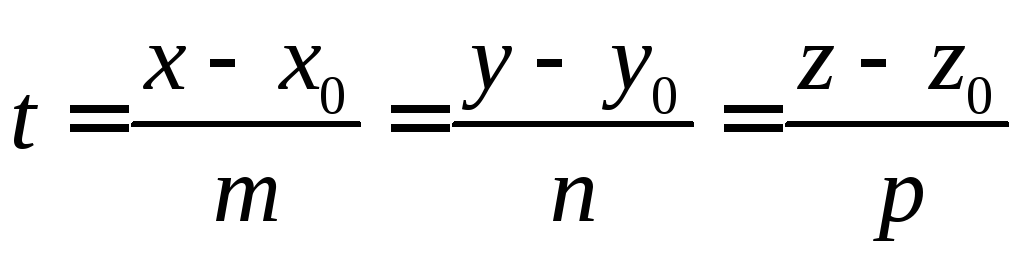Тогда (3.45)

(3.45) – канонические уравнения прямой в пространстве, то есть уравнения прямой, проходящей через точку параллельно вектору.

Заметим, что уравнения (3.45) задают прямую как результат пересечения плоскостей

,

одна из которых параллельна , а вторая –или как

где первая плоскость параллельна , а вторая –.

Если прямая проходит через две заданные точкии, тонаправляющий вектор этой прямой, поэтому из (3.45) получим:

(3.46)

(3.46) – уравнения пространственной прямой, проходящей через две заданные точки.

Угол между прямыми в пространстве

Рассмотрим прямые, заданные в некоторой пдск каноническими уравнениями:

и

.

ОПРЕДЕЛЕНИЕ. Углом между прямыми в пространстве называется угол между двумя пересекающимися прямыми, проходящими через произвольную точку пространства параллельно данным.

Из определения следует, что . Если, то

.

1) – условие перпендикулярности прямых.

2) – условие параллельности прямых в пространстве.

ПРИМЕР. Найти угол между прямой и прямой, проходящей через точкии.

.

Заметим, что уравнение прямой имеет вид:. В данном случае ноль в знаменателе писать принято: он означает, что направляющий вектор прямой (и сама прямая) параллелен плоскости. Эта прямая является результатом пересечения плоскостейи.