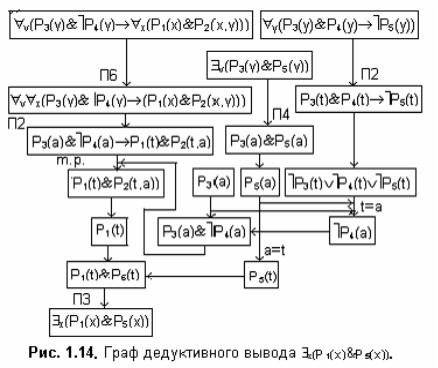
•F15= P1(t)&P5(t) - заключение по F4, F14 при t=a и правилу П1 и.в.,

•F16= x(P1(x)&P5(x)) - заключение по F16 и правилу П3

и.п. ч.т.д.

На рис. 1.14. изображен граф вывода x(P1(x)&P5(x))

1.2.2.5. Метод резолюции

Если матрица формулы в результате приведения ее к виду ПНФ не будет содержать сколемовских функций, то для вывода заключения полностью применим алгоритм метода резолюции исчисления высказываний. Однако, ес-

ли в результате приведения формулы к виду ССФ аргументы атомов будут содержать сколемовские функции, то для поиска контрарных атомов необходимо выполнить подстановку вместо предметных переменных аргумента атома новых предметных переменных или постоянных или функциональных символов, т.е. термов, и получить новые формулы дизъюнктов, которые уже возможно допускают унификацию контрарных пар.

Множество подстановок нужно выполнять последовательно, просматривая каждый раз только одну предметную переменную.

Принцип резолюции логики предикатов может быть усилен использованием информации о резольвируемых атомах.

Упорядоченным дизъюнктом называется дизъюнкт с заданной последовательностью атомов. Атом Pj старше атома Pi в упорядоченном дизъюнкте тогда и только тогда, когда j>i. Например, в упорядоченном дизъюнкте (P1 P2 P3 P4) самым младшим считается атом P1, а самым старшим - P4. При наличии в упорядоченном дизъюнкте двух одинаковых атомов, по закону идемпотенции, следует удалить старший атом.

Например,

(P1(x) P2(y) P1(x) P3(z))≡(P1(x) P2(y) P3(z)).

При соединении дизъюнктов, содержащих контрарные атомы, и формировании резольвенты нужно удалить из пары старший контрарный атом, а младший сохранить в резольвенте, выделив его рамкой. Например,

(P1(x) P2 (y)) ( ¬P1(x) P3 (z)) ≡ ( P1(x) P2 (y) P3 (z)).

При этом следует соблюдать правила:

a)если в резольвенте за обрамленным атомом справа не следует никакой другой атом, то обрамленный атом удаляют ,

b)если в резольвенте за обрамленным атомом справа следует какой-либо атом без рамки, то обрамленный атом оставить для последующего анализа,

с) если резольвента представляет собой один обрам-

ленный атом и он унифицируется с контрарным одноатомным дизъюнктом, то формируется пустая резольвента,

что свидетельствует об истинности выводимого заключения.*.

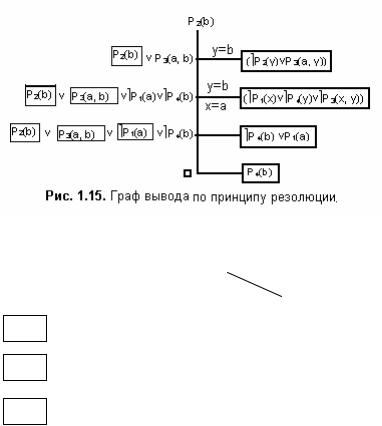
Пример 1.78. «Существуют студенты, которые любят всех преподавателей. Ни один из студентов не любит невежд. Следовательно, ни один преподаватель не является невеждой»[3].

Введем предикаты: P1(x):= «x – студент», P2(y):= «y – преподаватель», P3(x, y):= «x любит y», P4(y):= «y

– невежда».

Формула этого суждение имеют вид:

x (P1 (x) & y (P2 (y) → P3 (x, y))), x (P1 (x) → y (P4 (y) → ¬P3 (x, y)))

y (P2 (y) → ¬P4 (y)).

Вывод заключения:

•преобразовать посылки и отрицание заключения к виду ССФ:

F1= x(P1(x)&y(P2(y)→P3(x, y)))= y(P1(a)&( P2(y) P3(a, y))),

F2= x(P1(x)→y(P4(y)→¬P3(x, y)))= x y(¬P1(x)¬P44

(y)¬P3(x, y))),

* по материалам [3].

F3=¬ y(P2(y)→¬P4(y))=P2(b)&P4(b),

•выписать множество дизъюнктов посылок и отрицания заключения: K={P1(a), (¬P2(y) P3(a, y)), (¬P1(x) ¬P44

(y) ¬P3(x, y)), P2(b), P4(b)}.

Процесс вывода заключения по принципу резолюции представлен графом на рис. 1.15.

•Выполнить подстановку и унификацию дизъюнктов:

b

P2(b) ∫(P2(y) P3(a,y)=P2(b) ¬P2(b) P3(a,b)=

y

P2(b) P3(a,b)−резольвента,

b

P2(b) P3(a,b) ∫(¬P1(x)¬P4(y)¬P3(x,y))=

y

P2(b) P3(a,b)¬P1(x)¬P4(b)¬P3(x,b)=

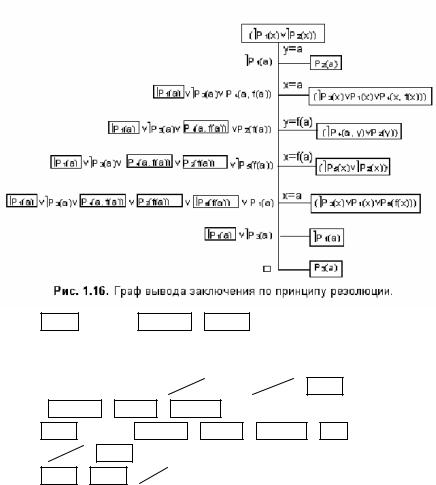
Пример 1.79. «Преподаватели принимали зачеты у всех студентов, не являющихся отличниками. Некоторые аспиранты и студенты сдавали зачеты только аспирантам. Ни один из аспирантов не был отличником. Следовательно, некоторые преподаватели были аспирантами» [3].

Пусть P1(x):= «x – отличник», P2(x):= «x – аспирант», P3(x):= «x – студент», P4(x, y):= «x сдает зачет y», P5(x):= «x – преподаватель».

Формулы этого суждения имеют вид:

x (P3 (x) & ¬P1(x) → y (P5 (y) & P4 (x, y))),

x (P2 (x) & P3 (x) & y (P4 (x, y) → P2 (y),x (P2 (x) → ¬P1(x)).

x (P5 (x) & P2 (x).

Вывод заключения (на рис. 1.16 изображен граф вывода):

• преобразовать посылки и отрицание заключения в ССФ:

116 Математическая логика

F1= x(P3(x)&¬P1(x)→ y(P5(y)&P4(x,y)))= x(¬P3(x) P1(x) P 5(f(x)))&

&(¬P3(x) P1(x) P4(x, f(x))),

F2= x(P2(x)&P3(x)& y(P4(x,y)→P2(y)))= y(P2(a)&P3(a)& &(¬P4(a, y) P2(y))), F3= x(P2(x)→¬P1(x))= x(¬P2(x) ¬P1(x)), F4=¬ x(P5(x)&P2(x))= x(¬P5(x) ¬P2(x)),

• выписать множество дизъюнктов:K={(¬P3(x) P1(x) P5(f(x))), (¬P3(x) P1(x) P4(x, f(x))), P2(a), P3(a), (¬P4(a, y) P2(y)), (¬P1(x) ¬P2(x)), (¬P5(x) ¬P2(x))},

• выполнить подстановку и унификацию дизъюнктов:

a

∫ (¬P1(x) ¬P2(x) P2(x)=¬P1(a) ¬P2(a) P2(a) = ¬P1(a) − x

−резольвента,

a

¬P1(a) ∫ ¬P3(x) ¬P1(x) P4(x,f (x))= ¬P1(a) ¬P3(a) x

¬P1(a) P4(a,f (a))= ¬P1(a) ¬P3(a) P4(a,f (a))−резольвента,

f (a)

¬P1(a) ¬P3(a) P4(a,f (a)) ∫ (¬P4(a,y) P2(y))= ¬P1(a) y

¬P3(a) P4(a,f (a)) ¬P4(a,f (a)) P2(f (a))= ¬P1(a) ¬P3(a)P4(a,f (a)) P2(f (a))−резольвента,

f (a)

¬P1(a) ¬P3(a) P4(a,f (a)) P2(f (a)) ∫ (¬P5(x) ¬P2(x))= x

¬P1(a) ¬P3(a) P4(a,f (a)) P2(f (a)) ¬P5(f (a)) ¬P2(f (a)) =

¬P1(a) ¬P3(a) P4(a,f (a)) P2(f (a)) ¬P5(f (a))−резольвента,

¬P1(a) ¬P3(a) P4(a,f (a)) P2(f (a)) ¬P5(f (a))

Приведенные примеры показывают эффективность вывода заключения по принципу резолюции, так как применяются только два правила: подстановки и унификации. Эти процедуры достаточно просто реализуются на компьютере, что позволило разработать формальные языки для логических задач.