
gorod-geom1
.pdf
оПТНБрТБТБММЕМПЗДМvЦЕОЙЕ 6.6 |
|
|
|
|
|
|
§ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
||||||||||||||||||
7→ÒÁÍÍv|||| ЕЧЛМЙДПЧБ1. |
, ЕУМЙ Й ФПМШЛП ЕУМЙ ДМС ОЕ£ ЧЩ ПМОСЕФУС ФПЦДЕУФЧП |
||||||||||||||||||||||
дПЛБЪБФЕМШУФЧПНЕФЙН, ЮФ ДМС. оЕПВИПДЙНПУФШМАВПКОПТНЩvПЮЕЧЙДОБ. юФПВЩ ДПЛБЪБФШ2 : |
ДПУФБФПЮОП(6УФШ,-7) |
||||||||||||||||||||||
|
|
||v + w||2 |
+ ||v − w||2 |
= 2 ||v||2n+ ||w|| |
|
|
|
n |
|
|
n |
|
|||||||||||
рПМБЗБС u = n |
|
|
|
|
|
· v; w) = n · (v; w) ДМС ПЙЪЧЕЧУИn Z É×ÓÅÈ v; w V . |
|||||||||||||||||
ДБООБС ТБЧЙМПН (v; w) def= ( |
7→ v|||| |
ÎÁ R ÆÕÎË ÉÑ R |
|
|
R |
|
- R |
||||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
Й ПМ ЦЙФ МШОБ. пЮЕЧЙДОП ФБЛЦЕ,||v + wÞÔÏ|| −(||v − w||) =4 УЙННЕФТЙЮОБ, ОЕЧЩТ ЦДЕОБ |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
w1) ХДПЧМ+=w2()v;=ФЧПТСЕФw(v;) =w1()v;+ПЦДЕУФЧХ(v;w)w2)v;: w(6-7),VФП. |
||||||||||||
éÚõÕ ТБЦОЕОЙЕÒ. 6(.23v1 +ЧЩФЕЛБЕФ,v26; w.23) =. рПЛБЦЙФ(vÞÔÏ1; w)(+n (vÞÔÏ2; w)ÅÓÌÉ−ОПТНБ(v;v; |
|
|
− |
|
|
|
− |
|
|
|
|
||||||||||||
|
( ·v;v,wЪБЛМАЮБЕН,)= (V; w) ЮФП=(v;(n w· u;) w) = n · (u; w), |
ФЛХДБ |
|
|
|
|
|
||||||||||||||||
уПНВЙОББЪБФАВБЫ |
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
Q |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
УФЧЕООЩНЙЕ(v;ФБНЙ: w)МЙОЕКОЩН.дМСППФОПД |
||||||
ìÅÍÍÁХЮОЙАЕМШУФЧБОПТНБПНЛ£ 6ЙСНМЙОЕКОЩН.1Х ТvФТВЙМЙО.6.23ХÅЛЬФФУСКОПУФЙПНВЙОБПЪОБЮБЕФПЙСНФОПЫЕОЙАУВЙМЙОЕКОПУФШТБЙПОБМШОЩНЙv;Л wМАВЩНVТ ЛПЬЖЖЙЧЕЭЕДЕОЙС |
|
|
|
|
|
||||||||||||||||||
Ë |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7→ |||| |
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
дПЛБЪБФЕМШУФЧП. пВv ПЪОБЮЙНОЕЮЕТТЕТЩЧОБЕЪei Ч УФБОДБТФОПК ФП ПМПЗЙЙ. |
|
|
|||||||||||||||||||||
ÏÌ ÖÉÍ M = maxi |
|
|
|
|
|
|
Rn УФБОДБТФОЩЕ ВБЪЙУОЩЕ ЧЕЛФПТЩ Й |
||||||||||||||||
|
|
||ei||. ПЗДБ ДМС МАВПЗП v Rn |
|
n |
|
|
|
|
|
|
|
||||||||||||
|| || |
|
|
|
|
6 |
| |
| · || |
|| 6 |
|
|
|
| |
| |
|
· || |
|| |
|
|
|
||||
|
|
X |
xiei |
|
|
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
рПЬФПНХ ДМСv |
|
|
|
|
|
ei |
|
nM maxi |
xi = nM |
|
|
v st : |
|
||||||||||
ЛБЦДПЗП= " > 0 ТЙ xi |
|
|
|
|
|||||||||||||||||||
ÓÔ×Ï |
|
|
|
|
|
|
|
||v − w||st < Ж = "=2nM ЧЩ ПМОСЕФУС ОЕТБЧЕО- |
|||||||||||||||
|
|| 6 || |
− |
|| |
||||||||||||||||||||
|| || − || |
|
· || |
− |
|| |
|
|
v;". w |
|
|
|
|
|
|
|
|
|
|||||||
йЪ МЕННЩv |
ЧЩФЕЛБЕФ,w дПЛБЦЙФv ЮФw <ТЙnMЖЙЛУЙТПЧБООЩИv w st < |
|
R |
|
|
|
|
|
|
|
|||||||||||||
( v; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
w) = (v; w) ОЕ ТЕТЩЧОЩ ЛБЛ ЖХОЛ ЙЙ |
|
|
|
|
|
БТЗХНЕОФБВЮБУФЙ ТБЧЕОУФЧБ |
|||||||||||||||||
ëÏÌØх ТБЦОЕОЙЕУЛПТП ПОЙ6ÓÏ×.24. БДБАФ ОБÅ ÜÔÏЧУАДХ. ДЙБЗПОМ ФОПНR |
ПДНОПR ЦЕУФЧЕФ2 |
|
|
R. |
|||||||||||||||||||
УПЧ БДБАФ ЧУАДХ. |
|
|
|
|
|
|
|
|
|
|
|
- |
|
|
|
|
Q R, ÔÏ ÏÎÉ |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
УЛЧБДТБФПЧЗПТ УФТБОУФЧÁМОБЪЩЧБЕФУСКБТБММЕМЧУАДХЗТБННБМПФОЩНТБЧОБ УХННЕ,УМЙЛЧБДТБЕЗПЪ- |
||||||||||||||||||
ФПЧНЩЛБОЙЕ12ХФЧЕТЦДБАЭЕЕ,ЮЕФЩТПДНОПЦЕУФЧПУПЧ£И ЕЗПБДБЕФУФПТПОФПУПЮФПЧУЕНМПЗЙЮЕУХННБТПУФТБОУФЧПН |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6.3.2. Ï ÏÌ |
|
|
УЛБС ЬЛ ЙЧБМЕОФОПУФШ ОПТН. вХДЕН ОБЪЩЧБФШ |
ÎÏÒ |
||||||||||||
|
|
|
|
|
|
|
||||||||||||
дПЛБЪБФЕМШУФЧПОЩНЙНЩ ОБ, ЧЕЛФПТОПНУМЙ ЙОДХПЗЙЮЕЙТПЧБООЩЕТ УФТБОУФЙНЙ×Е VНЕОБДФТЙЛЙПМЕНОБ RБЖЖФПЙООПНПМПЗЙЮЕУЛЙУФТБОУФЧЕТ ЬЛЧЙДЧЕБМЕОФ- |
||||||||||||||||||
|
ÄÁÀÔõ ÌÉÞÎТБЦОЕОЙЕПДОХÈ ÎÏÒÍÔÕ6.v25ÖÅ. рПЛБЦЙФНЕ ЮЕУЛХАÅ, ÞÔÏÒ ÄÌÑÔÏ ÏÌ ÇÉÀПЗЙЮЕÎÁ ÓËÜÔ К ЬЛЧЙЧБМÒ ЕОФОП ФЙ. Ä×ÕÈAÒÁÚ(V ) |
|||||||||||||||||
|
|
|
|
n |
|
|
|
|
v 7→ v||||2 ОЕ ВИПДЙНП Й ДПУФБФПЮОП, ЮФ ВЩ ЛБЦДПН |
|||||||||
|
|
ÔËÒÙÔÏÍ ÛÁÒÅ7→ v||||1 |
|
|||||||||||||||
|
|
ÔÙÊ ÛÁÒ |
|
|
{v V : ||v||1 < "} ЕТЧПК ОПТНЩ |
ДЕТЦБМУС ОЕЛ |
ÏÒÙÊ |
ÔËÒÙ |
||||||||||
мАВБСПТЕНБОПТНБ6.2{ÎÁv V : ||v||2 < Æ} ×Ô |
ÏÊ |
|
ÎÁÏÂ ÏÔ. |
|
|
|
|
|
|
|||||||||
ÍÙ v |
|
|
n |
|
|
|
|
|
|
|
ПЛБЪБФШ,ТФОПКЮФПsupДМС-ОПТНЕМАВПК(6-ПТ6)-. |
|||||||
|
|
|
|
R. уПЗМБУОПФППМПЗЙЮЕУЛЙХТ. 6.25,ЬЛЧЙЧБМЕОФОБДПУФБФПЮОП УФБОД |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
É M7→ÔÁË,v||||ЮФПВЩОБR ДМСНПЦОПЧУЕИ ПДПВТБФШv |
ЧЕЭЕУФЧЕООЩЕ ПМ ЦЙФЕМШОЩЕ ЛПОУФБОФЩ |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
Rn |
ЧЩ ПМОСМЙУШ ОЕТБЧЕОУФЧБ |
|
|
n (6-8) |
|||||
(Ч ЬФПН УМХЮБЕУФБОДБТФОЩК ·"||-ËÕÂv||stÓ6 ÅÎÔÒ||v|| 6ÏÍM× ·ТПЙЪЧПМШОПК||v||st |
ФПЮЛЕ p |
|||||||||||||||||
УПДЕТЦБФШ ЧО ФТЙ |
|
ПДЕТЦБФШВС"=M-ЫБТ ОПТНЩ v |
|
|
|
|
R |
ВХДЕФ |
||||||||||
|
|
|
ÕÄÅ= |
|
|
|
|
ЧОХФТЙ У ВС УФБОДБТФОЩКv Й, ОБПВПТ"=МБУОП-ЛХВ)Ф, ЛБЦДЩК. "-ЫБТ |
||||||||||
ЬФПКзТБОЙОПТНЩБ KВ |
|
|
|
|
|
|
|
|
7→ |||| |
|
|
|
|
|
||||
ЛПНЙС vБЛФОБ (Ч |
{v RÎÏÊ: ÔÏ||v||ÏÌst |
=ЗЙЙ),1} УФБОДБТЙОЕТЕТЩЧОБСФОПЗП1-УПЗЛХВБ |
МШОПЗЕОФТПНЕН.6.1 ЧЖХОЛЮЕОЙКОХМ- |
|||||||||||||||
M = vsup7→ |||| ДПУФЙЗ |
ÎÁ ÎÅÊ Ó×Ï |
И НБЛУЙНБМШОПЗ |
Й НЙОЙН |
|
Ï ÚÎÁ |
|||||||||||||
ÂÙ |
|
vЖХОЛЧЙЙ=KvinfПУМЕДПЧБФЕМШОПУФШv . ъБНЕФÉН, ЦДЕООПЮФvk > 0, ПУЛПМШЛХ |
|
ЮЕ УХЭЕУФЧПЧБМБ |
||||||||||||||
|
|
УИПДСЭБСУС|| || |
|
|
|
|| || |
|
|
|
|
|
|
|
|
|
|
||
|
|
K |
|
|
|
|
K |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ò |
|
ЧОПУФЙ |
|
|
|
v |
|
|
|
|
K ||vk|| → 0, ÞÔ |
× ÓÉÌÕ ÎÅ Ò |
||||||
klim |
|
|
|
|
7→ v|||| Й ОЕЧЩТДПЧБФ |
УФЙ ОПТНЩ ПЪОБЮБМ |
ВЩ ТБЧЕОУФЧП |
|||||||||||
ЧЕОУФЧБvk =0 |
0< K, ЮФП ОЕ ФБЛОЕТБЧЕОУФЧБ.уМ |
|
|
|
|
|
|
|
ÎÅÒÁ- |
|||||||||
|
|
|
|
ЕМШОП, ДМС ЧУЕИ w K НЩ ПМХЮБЕНЙНЕ |
||||||||||||||
→∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
МАВПЗП v |
|
6 ||w|| 6 M < ∞ . рПДУФБЧМСС Ч ОЙИ w = v=||v||st |
|
ÄÌÑ |
||||||||||||||
уИуМПДЙНПДУФЧЙЕУФШ6= 0Ч6ФТЕВХЕНЩЕ.НЕ2 ФТЙЮЕУЛПКПТДЙОБФОХАППМПЗЙЙ,(6ЪБДБООПК-8). |
ÎÁ |
n |
|
|
|
|
||||||||||||
6ФЕМШОПК.4. ÎÏчЩТНЩ,ЧХЛММАВПК)ПЪОБУФШЮБЕУЙУФЕНЕ. ч БЖЖЙООПНПЛБЖЖЙООЩИТ УФТБОУФЧЕЛППТДЙОБФУИПДЙНПУФШОБЪЩЧБЕ.ДЧRПМЕНЛБЛПКТЙ -ОЙВХДШВБТЙПНПЭЙЕОФТЙЮЕ(БТПЙЪЧУМДÏ×ÁÌØ- |
||||||||||||||||||
ЛПНВЙОБ ЙС ФПЮЕЛ x1p1 +x2p2 + |
|
|
|
|
R |
|
|
|
ÓËÁÑ |
|||||||||
ЕУМЙПДЕТЦЙФЧУЕ£ ПЬЖЖЙ ЙЕОФЩ xi · · · +xmpm (ÇÄÅ P xi = 1) ÎÁÚ |
|
ЧБЕФУС ЧЩ ХЛМПК, |
||||||||||||||||
Ó |
|
|
|
|
|
|
ПФТЕрПЛБЦЙФВБТУПЛМАВЩНЙ[p;Е,ЕОФТЙЮЕУЛЙЕqЮФП0=. жЙЗХТБДЧХНСДМСЧЩУЧПЙНЙХЛМПНВЙОБж УФЙПЮЛБНЙЖ ЗХТЩФУСМАВЩИpЧ,ОЕПВq ПОБХЛМПКУЧПЙИПДЙНППДЕТЦБМ,ФПЮЕЛЙУМЙДПУФБ.ПОБЙ- |
|||||||||||
|
х УТБЦЮОП,ДЙЧУЕОЙЕСАЭЙКЮФПВЩЧЩ6.ЙИ26ХЛМЩЕЧНЕУ. |
|
> |
|
|
|
|
|
|
|
|
|
||||||
{ p + q | + = 1; ; > 0} .

ХЛМЩИ ЖЙЗХТ, У |
ÉИ ДБООХА Ж |
|
ж , ОБЪЩЧБЕФУС ЧЩ ХЛМПК ПВПМПЮ- |
|||||||||
ЛПК ЖЙЗХТЩ ж ЙПДЕТЦБЭВПЪОБЮ |
ФУС onv(ж ). йОБЮЕ onv(ж ) НПЦОП П ЙУБФШ ЛБЛ |
|||||||||||
НОПЦЕУФЧП ЧУЕИ ЧЩ ХЛМ |
È |
|
|
ÓËÉÈ Ë |
НОПЦЕ |
|
|
|
|
|
||
чОХФТЕООПУФШ Й ЪБНЩЛÁОЙЕ МАВПЗ |
ЧЩ ХЛМПЗ |
òÉÓ. 6 Φ |
|
|
||||||||
ЧУЕЧПЪНП |
ЩИ ПОЕЮОЩИ О |
ÏÒÏ× |
ÞÅË Æ |
|
æ . |
|
|
|||||
ÓÔ×Á |
×Ù ÕËÌÙ. |
|
|
УМЙ ФПЮЛЙ a |
b |
|
|
|
|
|
||
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
||||||
рЕТФБЛЦЕП ЧЩФЕЛБЕФ ЙЪ ФПЗ , ЮФП |
|
|
|
|
|
|||||||
пЮЕЧЙДОП, ЮФП ЕТ УЕЮЕО ВБТЙЧЩ ЕОФТЙЮЕХЛМЩИ§ ЙЗХТХЖ ЙЗХТЩПНВЙОБЧЩХЛМ ЙК.рЕТЕУЕЮЕОЙЕ ЧУЕИ ЧЩ |
||||||||||||
|
ЧЩ ХЛМПН НОПЦЕ |
ж ЧНЕУФЕ У ОЕЛПФПТЩНЙ " |
|
|
|
|
|
|||||
|
|
|
|
|
|
|||||||
|
|
ak |
É b = lim bk |
|
|
|
|
|
b |
|||
рТЙНЕТМАВИ ЖЙЛУЙТПЧБОО→∞ И , НЩ ЙНЕЕНk→∞ |
klim ( ak + bk) = |
|
b, |
Ô |
||||||||
a + |
||||||||||||
|
|
|
ПЦЕЧУЕ"Ф-ПЮЛЙХВБНЙПФТЕЪЛБ(УН. ТЙУ[ab. 6УПДЕТ- |
|
|
|
|
|
||||
ЦБФУСЛХВБНЙЧBж"(a)НЕУФ; BЕЛБЕ"(b)У ФБЛЙНЙж ,УФЧЕ |
|
|
|
|
|
|
|
|
|
|||
чФПТПЕ ЧЩФ a =ФklimЙЪ |
ÏÇÏ, ÞÔÏ ÄÌÑ |
|
|
1). |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
ЖЙЗХТЩОПУФШ1ЧЩ. чОХФТЕОХЛМБПК.- |
||||
ЙЗХТЩХЛМБСФПЮЛБж6ПВПМПЮЛБ.,10ЕУМЙПФТ(УЙНЕЪЛБФБЛkПЧЩМЕЛ+1[a;ФУСbВУЩ)ПЮЕЛФБЛЦЕМЙapЙ0;СЧМСЕФУСbp.1; : :УЙН: ; pkМЕЛУПН,ТЕДЕМПНОЕЕЦБЭЙИПУМЕДПЧБФЕМШОПУФЙОЙЧЛБЛПК(k ФБЛПЮЕЛ |
|||
чЩЖМАВБС |
n |
→∞ |
|
|
n |
У ЧЕТЫ ОБНЙ Ч ЬФЙИ−1)ФПЮЛБИ-НЕТ- |
|
ЙОПКВПЪОБМ УЛПУЮБЕÔУСЙ, ОБЪЩЧБЕ[p0; p1; : : : ; pkk-=НЕТОЩН |
|
||
ФЧЕПТДЙОБФБИФУФЧЕООПОЩЕФТ.£(xИНЕТОЩЕ1; x2; : : : ;УЙНxn) МЕЛУЩОБЮБМПНУХФШЧ ПФТЕЪЛЙ,p0 ПФОП:УЙФТЕМШОПХЗМШОЙЛЙВБЪЙУБ(6-9) |
|||
eЙпДОПНЕТОЩЕ,i Ф=чФТБЬДТЩБЖЖЙООЩИУППДЧХНЛП |
n i=0 xipi |
i=0 xi = 1 ; xi > 0 o |
|
|
X |
X |
|
|
|
|
(6-10) |
|
|
|
|
ОЕТБЧЕОУФЧ−→p0pi i = 1; 2; : : : ; n , УЙН МЕЛУ (6-9) ЪБДБ£ФУС УЙУФЕНПК ЙЪ (n+1) МЙОЕКОЩИ |
|||
|
1 > 0 |
|
|
|
·n· · · · · |
|
|
|
|
|
|
x1 +>x02 +
Ô.Åõ. ФТЕООПУФШ,[СЧМСЕФУСpТБЦОЕОЙЕ1 ; p 2 ; : : :ÁÅÒ;6ÅÇp.27УЕЮЕОЙЕНmП ЗТБОЙ.УрТПЧЕТШФЕ,m <Бn(СЧМСЕФУСnÉ +i 1)ÞÔ ÏÌÕУЙНВЯЕДЙОЕОЙЕН· · ·ÒÌÅËП+УФТБОУФЧx[np06; pЧУЕЧПЪНПЦОЩИ11;::.: : ; pn ЙНЕЕФУЙНОЕ МЕЛХУФХАПЧ ЧЙДБЧОХ-
{0; 1; : : : ; n}.

рТЙНЕТ 6.11 (ЗЕПНЕФТЙЮЕУЛ Е |
ÎÏÒÍ) |
|
|
ФПрПУЛПМШЛХПМПЗЙА, ЧУЕДМС ОПТНЩМАВПК ОПТНЩБ ЧЕЛФvПТОПНП ЙУБОЙЕТ УФТБОУФЧЕ Rn ЪБДБАФ ПДОХ Й ФХ ЦЕ |
|
B1(0)7→= |
|||| £ ДЙОЙЮОЩК ЫБТ У ЕОФТПН Ч ОХМЕ |
МАВЩИУЙФПДЮvÅÌØÎ, wПТ,ЪБНЛОХФУÏДОПУФЙОХМС,БЙОПТНЩЙЪУПДЕТЦЙФОЕТБЧЕОУФЧБЧЩФЕЛБЕФ,ОХМШv ЧФТЕХЗЮФПVЛБЮЕ:ЬФПМШОЙЛБУФЧЕv ЫБТЧОХФТ1|ЕОФТБМШОПЮФОЕКПОПЮЛЙЧЩУЙННЕФТЙЮЕО.ХЛМЩК:(6-ДМС11) |
||||||||||||||||||||||||||||
ÏЗТБОФОПйЪ |
|
|
|
|
|
|
|
|
|
{ |
|
|| || |
6 |
} |
|
|
|
|
|
|
|
|
|
|
||||
|
|
||v||; ||w|| 6 1 Й МАВЩИ ; > 0 |
+ = 1 ЙНЕЕН |
|
|
|
|
|
|
|
|
|||||||||||||||||
оПТНБ v |
|
|
|
|
|
|| v + w|| 6 ||v|| + ||w|| 6 1 : |
|
|
|
|
|
|
|
|
|
|||||||||||||
7→ v|||| ПДОПЪОБЮОП ЧПУУФБОБЧМЙЧБЕФУС П ЕДЙОЙЮОПНХ ЫБТХ (6-11) ЛБЛ |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
жПТНХрТЕОФТБМШОПДМÙЦЕОЙЕ(6ПН-11)БЛФБНЙ6.7(6-12)||v||ХУФБОБЧМЙЧБАФ=inf(R>0 |ВЙЕЛ1v ЙАBНЕЦДХ1(0)) : ОПТНБНЙ |
|
Á |
(6-12) |
|||||||||||||||||||||||||
дПЛБЪБФЕМШУФЧПХЛМЩНЙ |
|
|
|
× |
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R ПЮЛЙЧЩ- |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
ЮФ ЖХОЛ ЙСУЙННЕФТv . у ХЮЮОЩНЙ£RÔ , УЛБЪБООПЗДЕТЦБЭЙНЙФОПУЙФЕМШОПЧЩЫЕ,ОХМШОХМСОБНЧ.ЛБЮЕУФЧЕПУФБ£ФУСЧОХФТПМШЛПЕОÎЕКТПЧЕТЙФШ,Й |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
ДПЧМ=ОЕЧЩТinf(ФЧ ТСАЭЕНХ>0 v ХУМПЧЙАж ) , оЕТБЧЕОУФЧПДОПУФТПЕООБЕНЩ,ÑЧМСЕФУСП МАВПНХОПТНПКЧЩ |
|||||||||||||||||||||
ОБХЛМnÍÕ ÏÍ ÁËÔÕ7→æv||||ÓÔØ,æÕ |
|
R |
| |
|
|
|
|
|
|
|
|
ÓÔØ ÜÔÏКФТЕХЗПМШОЙЛБЖХОЛЙЙ ДП- |
||||||||||||||||
ПЮОП. рПМЙЪЧЩТПЧЕТЙФШЦЙФХЛМЕМШОПУФЙ:ТЙ n = 1, |
ЦДЕООППОЙУФШПЮЕЧЙДОЩПДОПТ. |
|
||||||||||||||||||||||||||
ФБФДХЕR |
|
|
|
|
|
|
|
|
|
|
|
|
|
v + |
|
|
|
|
|
|
|
|
w |
|
|
|
||
q = |
v |
w |
|
|
|
v; w V ФПЮЛБ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
= ||v||æ |
|
|
· |
|
|
|
||w||æ |
|
|
· |
|
|
|
|
|||||||
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
+ КwВБТЙж Е ФТv жЮЕУЛПК+ w ЛПНВж vОБж ЙЕК МЕЦБЭЙИv ж + ЧwжжФПЮЕЛw v=ж |
|
|||||||||||||||||||||||||
СЧМСЕФУС ЧЩ||v||ÕËÌæ |
|| || |
|
|
|| |
|| |
|| |
|| |
|
|| |
|| |
|
|| |
|| |
|| |
|| |
|
|
|| |
|| |
|
|
|
||||||
É w= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||v||æ |
||
|
|
ÏÍÕ q ÆÕÎËæ , .ЙПОБМЩÅ. q æ. тБУУНПФТЙН1É v + w БЖЖЙООПЕж v ж +ТПУФТБОУФЧПw ж . |
|
|||||||||||||||||||||||||
6||.4w.||1æ. .бЖЖЙООЩЕðÏÜÔ |
|
|
|| ||n |
6 |
|
|
|| |
|
|| |
6 |
|| || |
|| |
|
|| |
|
|
|
|
||||||||||
ЖХОЛПТДЙОБФn-ЙПОБМНЕТОЩН ЧЕЛФПТОЩН ТПУФТБОУФЧПНA = A(VV) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
ПОБМП |
ÎÁ |
|
|
|
|
|
|
|
|
|
|
|
|
R . вХДЕН ОБЪЩЧБФШ БЖЖ |
ÅÍÅ |
|||||||||||||
|
(x1; x2;A: : :БЖЖЙООП; xn) У ЕОФТ ВТБЦЕОЙЕЛБЛПК-ОЙВХДШ:A |
ФПЮЛЕR. чpБЖЖЙООПК УЙУФ |
|
|||||||||||||||||||||||||
|
|
ЙНЕЕФ(x)ЧЙД= (x) + |
= 1x1 + 2x2 + |
|
|
|
- |
|
An |
|
ЙООЩК |
|||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||
ÇÄÅ = D = ( 1; 2; : : : ; n) |
|
|
|
|
|
|
|
· · · |
+ nxn + ; |
|
|
|
|
|
|
|||||||||||||
ОЕЛПФПТПЕ ЮЙУМП. |
|
|
|
|
|
|
V | МЙОЕКОБС ЖПТНБ ОБ V , Б = (p) R | |
|||||||||||||||||||||

пЗТБОЙЮЕОЙЕ МАВПЗП БЖЖЙООПЗП §ЖХОЛ ЙПОБМБ : |
An - R ОБ ТПЙЪЧПМШ- |
|
ОЩК ПФТЕЪПЛ [a; b |
n |
|
ОБЛМАЮБАЭЙЕЬФПН ПФТЕЪЛДТХЗУФЧЕООП.ДТХЗБпЮЕЧЙДОП,A ЧПЪНПТЕДУФБЧМСЕФЮФЦОП(УФЙ:ДМСx) =УФБЛПКВПАx +€ЖХОЛЫЛПМШОХАЙЙ ЙНЕАФУСМЙОЕКОХАУМЕДХАЭЙЕЖХОЛ ЙА•ЙУ-
|
◦ |
ФПЦДЕ |
ВТБЭБЕФУС Ч ОХМШ |
|
|
|
|
|
|
|
|
◦ |
ЧППВЭЕДБМШОЕКЫБВТБЭБЕФУСПЧОПОХМШ Й ЙНЕЕ |
ОБ ЧУ£Н ПФТЕЪЛЕ ПУФПСООЩК ЪОБЛ |
|||||||
|
|
ВТБЭБЕФУСФУС |
ОХМШСБМШФТЕТОБФЙЧБ:ПДОПК ФПЮЛЕ x0 |
|
[a; b , |
É × ÜÔÏÍ |
УМХЮБЕ |
|||
|
◦ ÉÍÅ |
|
|
|
|
n |
|
|
||
|
n |
|
|
|
|
|
|
|
|
|
|
|
◦ x0ЕТЧБМСЧМСЕФУС[a; b ПДОЙН ЙЪ ЛПО ПЧ Й ЙНЕЕФ ПУФПСООЩК ЪОБЛ ОБ ПМХЙО- |
||||||||
|
|
|
r x0 |
n |
|
|
|
|
|
|
éÚ: |
|
|
ЬФЙ ОЕЪОБЛЙПУФЪОБЛСООЩНТПФЙЧПОБЛБЦДПНПМЖЖЙООЩНЙЪ1 ПМХЙОФЕТЧБМПЧЖХОЛЙПОБМПН |
|||||||
|
ЬФПЗП◦ [aЧЩФЕЛБЕФ,a;<x0x)0 Й<(bx0ЙЮФП; b ,ЙНЕЕФУТЙЮЛБЦДЩН£НПУФПСООЩК |
|
|
|
|
|
|
|||
ПВЯЕДЙA |
ÎÅÎÉÅRБЖЖЙОУЧСЪБÎÏКТБЪВЙЕОЙЕЗЙHЕТ =МПУЛПУФЙБЖЖЙООПЗÏ Ò ÓÔÒ |
ОУФЧБ A |
|
Ч ДЙЪЯАОЛФОПЕ |
||||||
|
|
- |
|
|
|
|
|
|
|
|
ЗДЕ ПВТБЭБЕФУС Ч ОХМШ, Й ДЧХИ {ЧЩp ХЛМЩИA | (ПФЛТЩФЩИp) = 0} ; ПМХ ТПУФТБОУФЧ |
||||||||||
|
|
|
n |
É H− |
|
n |
|
|
|
|
|
|
H◦ + = |
|
H◦ − |
= |
|
|
|
|
|
УПЮЛВЭЕК ЗТБОЙ ЕК {p Rn | (p) > 0} |
É |
{p Rn | (p) < 0} |
(6-13) |
|||||||
ЛТЩФЩИТБЪОЩИЕ,ЛПФПМХЛHЩФЩИ+СТП=СЧМСЕУФТБОПМХÓФЧСТПУФТБОУФЧБИЧОХФТЕООЕК(6-13)− СЧМСАФУС=H .ПЮЛПКрЕÒЪБНЛОХФЩЕЙУЕЛБЕЬФПНЬФПЗПМАВПКЗТБОЙПФТЕЪЛБПМХХ .HТПУФТБОУФъБНЩЛБЕЪПЛЧ ЕДЙУЛÎПОЙСНЙБНЙУФЧЕООПК- |
||||||||||
|
|
H◦ + = H◦ |
|
|
|
|
|
|
|
|
ьФП ЪБНЛОХФЩЕ ЧЩ{pХЛМЩЕR | НОПЦЕУФЧБ(p > 0}СЧМСАФУСПВЭЕК=ЗТБОЙ{p RÅÊ| (Hp)+6=0} :H |
(6-14) |
|||||||||
|
|
ЦЕОЙЕПМХФЛТЩФПЗП6Т.ПУФТБОУФЧБ8 ЧЩТБЪНЕТОПХЛМПЗ(6-13) НОПЦЕУФЧБЧ UФПЮОПУФЙЙМАВПКЙИФПЮЛЙЧОХФТЕООПУФСНЙp = H , .Й |
||||||||
äÌÑðÒПФЛТЩФЩЕÄÌÏМАВПЗ |
n |
|
|
|
|
|
− |
|
||
ЖЙООПН Т УФТБОУФЧЕ |
|
|
|
|
|
6 U × ÁÆ- |
||||
ТСНБС,1Ч ЮБУФÎЕПУФЙ,ЕТЪОБЮЕОЙСЕЛБАЭБСAОБUЛПО. БИ ПФТЕЪЛБУФЙ nПФМЙЮОЩ> 2 УХЭЕУФЧХЕФПФ ОХМС Й ТПФЙЧПТ ИПДСЭБПМ ЦОЩС ЮЕТЕЪП ЪОБЛХp
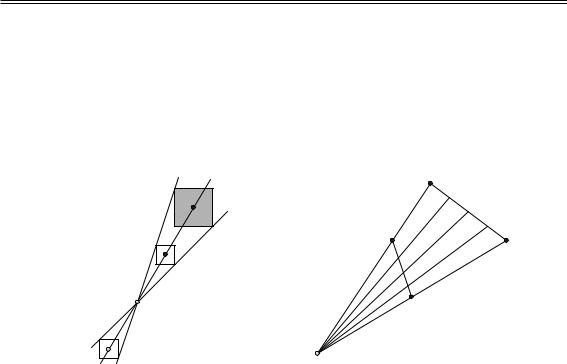
дПЛБЪБФЕМШУФЧПЩИ1 МХЮЕК.УпВПЪОБЮЙНОБЮБМПН Ч pЮЕТЕЪ. йЪ ТЙУC . 6An ПТВЯЕДЙОЕОЙЕПЮЕЧЙДОП,ЧУИЕТУФЙЕЛБАЭЙИЕЛБЕ U
ËÒÙÔПК ЧЩ ХЛМПК ЖЙЗХТПК. лТПНЕ ФПЗП,2p{ ТЙУ. 6 3 ЮФП CСЧМСЕФУС ЮЕТПЮЛБНЙМАВБСЕЛБЕC,ФБЛ,ТИП ЮФПДТХЗХАСЭБСЧУЕЮЕТЕЪФПЮЛЙУФПТПОХp` ТСНБС|П ПДОХЧОЕЫОЙНЙ` УФМЙВППОХФЧПCПЮЛБНЙ,ВЭЕФЙЪp СЧМСАФУСОЕЧЩC (УНХЛМПЕТЕ.ТЙУЧОХФТ.6УМCЕООЙНЙ,ДХЕФ,МЙВП
2).
|
u1 U |
|
[u1, u2] U |
u U |
c1 C |
|
u2 U |
c |
|
p |
c2 C |
˘
C
|
|
p |
|
ÅÒ. УФЧХАФЕЕЛБАЭХАтЙУ. рХУФШ. 6C3.q÷ÙТСНХА,| ПДОБХЛМПФМЙЮОХАÓÔØÉÚ CÎÉÈ. . ðÏÔ- |
|
УЛчТСНПКПМШЛЮБУФОПУФЙ,тЙУХ. 6(nqp2>.).пФЛТЩФПУФШ1оБЧОЕЫОЙЕЮЕТЕЪЗТБОЙЮОХАОЕКqВНПЦОПДМСДЕФC ÉCФПЮЛБÎÅФПЮЛЙТПЧЕУФЙХУФПФБr ÓÕÝÅC |
|
|
Ф. .ДУФЧЙЕПДЕТЦЙФ |
ДМС C ФПЮЛХ rC. рТСНБС (pr) ОЕ ЕТЕУЕЛБЕФ C U, |
|
óÌÅеУМЙЧЩдПЛБЪБФЕМШУФЧПЗЙ ЕТХЛМБЖЖЙООБСМУЛНОП6ÔÉÖÅ.3 ЛУФЧП.ПТБЪНЕТОПМУФТБОУФЧПНрПНЕУЛUУФШ,ЙНУФЙПОБ(ЧПЪНПЦОПОБЮБМП1УПДЕТЦЙФУС.ЛПДЕ(ЧПЪНПОХМШНЕТОБС)6=ДЙОБФp.Ч ОЕЛПФПТПКЧОХФТШОЕ ЕТЕУОЕУФТБОУФЧПЙЕЛБЕЕТНОПЦДЕУФЧЙНУЕЛБАЭЕКФПФЛТЩФПЕUУ
ЧЕЛФПТОЩНИ ДППДПМОЙФТ |
|
|
n |
n |
|
|
|
||
H W |
R |
ЦОП ОХМЕЧЩН). ч |
ЦЕУФЧЕЛБЦЕН,ЧУИ |
||||||
|
|
Ó |
|
||||||
УУНПЕНТФТЙНМАВЕЛФЙТХАФУСЛБЛ-ОЙВХДШЕМШОПЕЪЛЙ,НБЛ R |
|
|
|
|
|||||
|
|
|
ЙНБМШОПЛ HЕЛФЙТХЕНПД, УТ ПУФТБОУФЧПЧЛМАЮЕОЙАÒЦБЭЙИ WH ЙПДОЕ ТПЕТЕ ЕЛБАЭЙИH.UчЩВТБУ- |
||||||
ÞÔ dim H |
|
|
|
|
|
|
|
′: H H′ = Rn |
|
ЧЩ ХЛМПП |
′НОПЦЕУФЧ ФТ,ОЕ УПДЕТЦБЭЕЛХВЩ |ОХМС,ЕЛБЕnХВЩ,ОБ.H.UH′ УДПМШТ ЕЛФЙТХЕФУСH. рПУЛПМШЛХЧПФЛТЩФПÏФТЕЪЛЙ |
||||||||
|
= 1. äÌÑ ÜÔÏÇ |
Ó Ò |
|
|
R |
|
|
|
|
ФП ТЕЛДМ. 6.ЧЩВ8H |
|
|
|
|
|
∩ U = . åÓÌÉ dim H′ > 1, |
|||
ÝÅÅ Ò |
|
U. ÏÇ′ ÄÎÁКДH£ФУС ПДОПНЕТОП |
ПД ТПУФТБОУФЧПМШЫЕ,L ОЕ ЕТЕУЕЛБА- |
||||||
ТПФЙЧ ТЕЮ |
ÏÒÕ H . |
L ÎÅ ÅÒ |
U |
ÏÇ Â |
ÞÅÍ H, ÞÔÏ |
||||
1Ф. Е. У ЧЩЛПМПФЩН ОБЮБМПН |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|

çпЙ ТЕТДЕМЕОЙЕМПУЛПУФШ6H.8 (ÏОБЪЩЧБЕФУСПТОЩЕ ЗЙÏ ÅÒПТОПК§ МПЗЙ ЕТУФЙ)МПУЛПУФША ЖЙЗХТЩ ж |
Rn, |
||||||||||||
юЕТУМЙ ж |
+ |
|
|
|
|
|
|
|
|
|
|
||
дПЛБЪБЧЕУФЙПТЕНБЕЪ ПЛБЦДХАПТОХАЕМШУФЧПH6.3ЙЗТБОЙЮОХАЗЙH. еУМЙЕТ∩ МПУЛПУФШж ж6=ФПЮЛХ. . np МАВПЗПНЧЩПДЕТЦЙФУСХЛМПЗ НОПЦЕУФЧБ ж НПЦОП ТП |
|||||||||||||
ЧМПДОПКУЛ УÔЗЙЙ, ЕТ ПОБМУЛФЙЧОПНУФЙ,ВХДЕ R |
|
|
|
|
+ |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
|
|
|
ÔÏÏÏТОПКХ Т..ЕМЙЛ6еУМЙ.27ЧОХФТУж УФШОПУФШ(n +Ч1)ЛБЛПКФПЮЕЛ,-ОЙВХОЕ МЕЦБЭЙИШЗЙЕТ |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
æ◦ |
|
p ÇÉ ÅÒ Ì ÓË ÓÔØ H |
ЕТЕУЮЙЕЛБАЭХА |
|
|
|
|
|
6= . рТПЧ Д£Н ЮЕТЕЪ |
||||||
|
|
|
|
|
|
|
|
ТБЪЙПÎБМПЗПЙЪHЪОБЛБЙНЕФЧОХФТОБжЪЛПН,ПУФПНЩ- |
|||||
СООЩКПМХЮЙНЪОБЛЬФПН(ЧТППФТЕЪЛЦЕНОХУÌХШ ЖХОЛБЕУФТБОУФЧЕЙПОБМБ,ДЙЙЧж◦ . жХОЛПЮЛЙ.Е.ФПЮЛХ |
◦ |
|
|||||||||||
ОХЦОП, |
ЪБНЛОХФ, НЩ НП |
|
|
ÁÔØ, ÞÔ |
|
|
|
|
|
∩ж ). нЕОСС,ЕООП МЙ |
|||
|
|
|
|
|
|
|
æ◦ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
H . ъБНЩЛБОЙЕ |
ÓÔ |
||||
æ◦ |
МЕЦЙФ Ч |
ÏÍ ÏÌÕ ÒÏ |
|
|
|
H+ , Б ж МЕЦЙФ Ч ЪБНЩЛБОЙЙ ж◦ . |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
|
|
ЛБЦДБ4 ОУФЧБ,УФЙ,.. ЧЩрТЙНЕОССУПДЕТЦБЭЕЗБХЛМПЪОБЮЙНОПЦЕУФЧПФЙОДХЛ,ПЮЛБЙНЕЕФZЙА,ОЕНЩZПХСЧМСЕФУСНПЦЕНТБЪНЕТУФХАЧОХФТУЮЙФБФШ,ПУФЙЕТЕУЕЮЕОЙЕНЕООПОБЙНЕОШЫЕЗУФШЮФПДОПН.рПЛБЦЕН,ZУЧПЙИОЕБЖЖЙООППДЕТЦЙФППТОЩИЮФЧ |
|||||||||||
УСЗдПЛБЪБФЕМШУФЧПчУСЛПМХЕПТПДЗЙЕНБТ ЪБНЛОХФПЕТЕТУФТБОУФЧ6МПУЛП. |
|
|
|
|
|
|
|
|
|
|
|
||
ОЙВЬФПНПМÕДШУМХЮБЕТЧОХФТЕООЕКУФТБОУФЧНОПЦЕУФЧБСФПЮЛПКЧОЕЫОССp Z. дМСq |
|
|
|
+ |
|
|
ÏÊ- |
||||||
|
|
|
|
|
|
ЬФПЗ6Z ПМШЛОЕЕЦЙФДЙОЙНИПФСq УФТВЩЕЪЛЧ УФТБОУФЧП[q;ЙЪp П ЛБЛПТОЩИ |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
Z |
ЗТБО ЮОПК ПЮЛЛТБКОЙЕr |
Z◦ |
ТПЧЕД£Н П ПТОПЕЦЙФ ПМХ Т |
H+ Ë |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(p) > 0 É (r) = 0 ÓÌ ÄÕÅÔ,[q;ÞÔp ∩ (Zq.) рПУЛ< 0, Ф.ЕЮЕОЙЕ.q r М |
|
|
|
ПЗ ЧОХФТЙ [q; p , ЙЪ |
|||||||||
ЦБЭЕЗОЙЗТБж У |
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
ОБЪЩЧБЕ6рПДМАВПКШ.4ФПЦЕ.2ЬФХ. зТБОЙФУСЕ£СЧМСЕФУСЗПТБЪНЕТОППТОПКШЙоХМШНЕТОЩЕ.пФНЕЪБНЛОХФЩНЗЙУФЙН,ЕТОБЙМПЮЮФПУËЕОШЫЕЗПУФШАЙЧЩТБЪНЕТОП. рЕТХЛМЩНОБЪЩЧБЕУБЖЖЙООПЗУФШНОПЦЕУФЧМАВФУСHЪБНЛОХФÏÞËÉ)ЗТБОША.К ЗТБОЙД.ПКТтБЪНЕТОПЖЙЗХЧЩУФТБОЖЙЗХТЩХЛМФЧБ,ПКжУФШАж.ЖЙЗХТЩчУСЛБСПДЕТЗТБ |
||||||||||||
ЦЕУФЧП |
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
ОБЪЩЧБАФУСЕЛБЖЖЙООПЗОБЗТБОЙÏМШОЩНЙОФЙОХБМШОПППЩФЕПОЙНБАФУСЧЩЧЕТЫЙОБТБВТСЦЕОЙЕПДХЛМЩФЩНОПТ |
|
|
|
|
|
|
|
|
|
ÏФЕ-УОПЧБООПФЙНЕЕФУСФПЮЛБНЙТПЙЪЧ |
|
||||
|
|
|
|
|
|
|
|
ОБЙНЕОШЫЕЗ |
|
||||
ÍФБЛНЙУФТБОУФЧБ,ЙОПЗ.йОФХЙФЙЧОПЪБНЛОХФЩНЙПЧЩЕПЗТБООЙЛБНЙ,НЕОШЫЕЗТБОЕКЧОХФТПЮЛЙУПДЕТЦБЭЕЗnЧНОПЦЕ.ЧУОЙНЙ,УЙОДХОЕПОЙТЦБОЙЕЧУЙТПЧБФЧБНЙЧОЕЫЕЗДБОХМШНЕТОЩ,ЬФХЗТБОШФЕТНЙОБ.ЙНЙДЕЛЧБФОПОПКЗТБОЙоБФП.ТЙНЕТ,ЗТБОЙЮОЩНЙ(ФПМПЗЙЙХ€З.ЖТЙ.БОШ•,ЙЗХТЩТБВЫБТБ |
|
|
|
(ЗМБДЛ Е У |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|

ОЕФТЕЪЛПЧСЧМСАФУСПЧБМБНЙ)ТБОСНЙЙНЕАУБНПКУСЖЙЗХТЩПДОПНЕТОЩЕ. ЛЙНЗТБОЙ,ПВТБЪПН,ОХМШНЕТОЩЕ ЗТБОЙЪБНЛОХФП ПТЩИПК |
|||||||||||
ÏÞËÉ, Ô |
ÒÙЕ ЧПЪОЙЛБАФ |
ЛБЛ ПУМЕДОЙЕ ОХМШНЕТОЩЕ ЬМЕНЕ ФЩ ЧП ЧУЕЧПЪ- |
|||||||||
НПЦОЩИ Е ПЮЛБИ ЧЙДБ: ЖЙЗХТБ ж , ЗТБОШ |
ЖЙЗХТЩ ж , ЗТБОШ |
ЖЙЗХТЩ ж |
|
||||||||
ЧЩ ХЛМПК ЖЙЗХ |
æ ÍÏÖÅ |
|
ÎÅ ÂÙÔØ |
ÎØÀ ÄÌÑ æ . |
ÚÁ |
ÏÊ |
|||||
ЗТБОШ ЗТБОЙ ЗТБОЙ ЖЙЗХТЩ ж , . . . |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
-, |
|
|
|
|
|
|
|
|
|
|
ОЙЗТБЗДБУМЙБЮЕВЩЙЪ |
|
|
|
|
|
|
|
|
|
|
ÏÄÅÒ |
|
|
ÍÏПКОБУСФЦЕФ.ДЖЙЗХТЩЧУМЙОЕ.жФПЮЛПКЗТБОШВЩФШСЧМСЕФУСПЛБ.чВБУБНПНТБЪНЕЛПОжЧОХФТЖХОУ.ПДЕТЦБЭЕЗНПрПЛБЦЧОХФТЕООЕКБПЮЛБДЕМЕ,ОПУФШЕООЕКЬФПЗЙПОЕБМpФПЮЛБ,ЗТБОЙНЕОСМФТУСЦЕжДМСОБЪЩЧБАФУСЧЪЛБПЮЛПКСЧМСЕОЕВУжВЩжПМШЫЕНБФ, ОБФТЕЪЛБ,ЦБЭБОЙЛЦЕПЛБЪБФШУСОЙЛÎÕÌÑДМПЮЛЙЛТБКОЕКОЛТБКОЙНЙЕЦБФПЗПБИЧОХФТЙЗТБОЙ.оБППФТЕЪЛБОХМШНЕТОПКpОБВПТжПЗДБЕЦЙФЕЪЛОЙЛБЛФПЮЛБНЙ, Ф,ЗТБОЙЪ,ЦЕОББЛДПЗУЛТБКОЙЕЕМЙЛЗТБОЙСМШЛПФТpОЕПНСЧМСЕФУСЕЪЛБВЩМЛОХФ(ЙУ, |
|||||||||||
×ПОЙжЦБЭЕЗЧЩЩУЕЛБАЭЙКОХФТЕООЕКПЗДБ,ПТОЩН)жПМШЛОЕХЛМЙ |
|
|
|
|
|
|
|
|
|
|
|
. рПЬФПНХ ФПЮ |
p |
|
|
ЛТБКО |
|
|
ЗТБОША |
Õ |
|||
х ТБЦОЕО Е 6.28. |
ÇÒ |
ÎÉ Å, ÞÔÏ |
|
МАВ ЗТБОЙ ЪБНЛ ХФПК ЧЩ |
|||||||
æ , ÎÉ ÇÒÁ æ , ÎÉ |
|
ЗТБОЙ ж Й Ф. . |
|
ФПЮЛЙ, |
|||||||
ЛТБКОЙНЙ ФПЮЛБНЙ), Й ТЙЧЕÄÉÔÅ ÒÉНЕТ ЖЙЗХТЩ, ЙНЕАЭЕК |
|||||||||||
ХЛМПК Ж ЗХТЩ ж СЧМСАФУС ЛТБКО НЙ Й ДМС ж (Ч ЮБУФОПУФЙ, ЧУ |
ЧЕТЫЙОЩ СЧМС- |
||||||||||
П МЙЮОЩЕ ПФ ЧЕТЫЙО. |
|
|
|
|
|
|
|
|
|
||
рТЕДМПЦЕОЙЕ 6.9 |
ЪБНЛОХФБС ЧЩ ХЛМБС ЖЙЗХТБ СЧМСЕФУС ЧЩ ХЛМПК ПВПМПЮ- |
||||||||||
чУСЛБАФУСПЗТБОЙЮЕООБ |
|||||||||||
ПК УЧПЙИ ЛТБКОЙИ ФПЮЕЛ. |
|
|
|
|
|
|
|
|
|
||
ЛТБКОЙЕМАВПКАФУСЧЩÑ×ÌÑ Т ПЮЛЙИПДСЭЕКХЛМЩНЙЗТБОЕКПКЮЕТЕЪПНВЙОБСЧМСАФУСПНВЙОБp ТСНПКЙЕКЙСНЙЛТБКОЙНЙЛПО.ьФЙПЧ ПФТФПЮЛБНЙЕЪЛБ,ЩФПЮЕЛМЕЦБФЧЩУЕЛБЕНПЗПЙЬФЙИОБДМСЗТБОСИЗТБОЕКж . ЖЙЗХТПКЙ.рППЙОДХЛХТж. 6.ЙЙОБж28◦ дПЛБЪБФЕМШУФЧП. йОДХЛ ЙС П ТБЪНЕТОПУЛТБКОЙИ. мАВБС ЧОХФТЕООСС ФПЮЛБ p


