Метод непосредственного интегрирования

Метод непосредственного интегрирования, при котором данный интеграл путем тождественных преобразований подынтегральной функции и использовании свойств неопределенного интеграла приводится к одному или нескольким табличным интегралам.

Свойство инвариантности неопределенного интеграл

Таблица интегралов сохраняет свое значение, если под х принимать любую непрерывную дифференцируемую функцию от независимой переменной. Если , то и, где– произвольная функция, имеющая непрерывную производную. Таким образом, путем формальной заменых на u можно получить обобщенную таблицу простейших интегралов: ;, гдеu – любая непрерывная дифференцируемая функция от независимой переменной. Выбирая различным образом функцию u, можно расширить таблицу простейших интегралов: Например, , заменяях на lnx, получим .

Метод замены переменной (подстановки)

Этот способ заключается в переходе от данной переменной интегрирования к другой переменной для упрощения подынтегрального выражения и приведения его к табличному виду. В интеграле сделаем подстановку, где функцияимеет непрерывную производную. Тогда:на основании независимости неопределенного интеграла от выбора аргумента (§ 7.4):– формула замены переменных в неопределенном интеграле. Иногда целесообразно подбирать подстановку в виде, тогда, где .

Метод интегрирования по частям

Интегрирование по частям состоит в том, что подынтегральное выражение заданного интеграла представляется каким-либо образом в виде произведения двух сомножителей u и dv (это, как правило, можно осуществить несколькими способами); затем, после нахождения v и du, используется формула интегрирования по частям.

Если u=u(x) и v=v(x) – дифференцируемые функции, тогда d(uv)=vdu+udv, откуда udv=d(uv)-vdu. Интегрируя последнее выражение, получаем:– формула интегрирования по частям, которая применяется в тех случаях, если интеграл в правой части более прост, чем исходный. Эта формула дает возможность свести вычисление интегралак вычислению интеграла, который может оказаться существенно более простым, чем исходный.

Решение задач

Найти интегралы

1. .

2. .

3. .

4. .

5. .

6. .

7. .

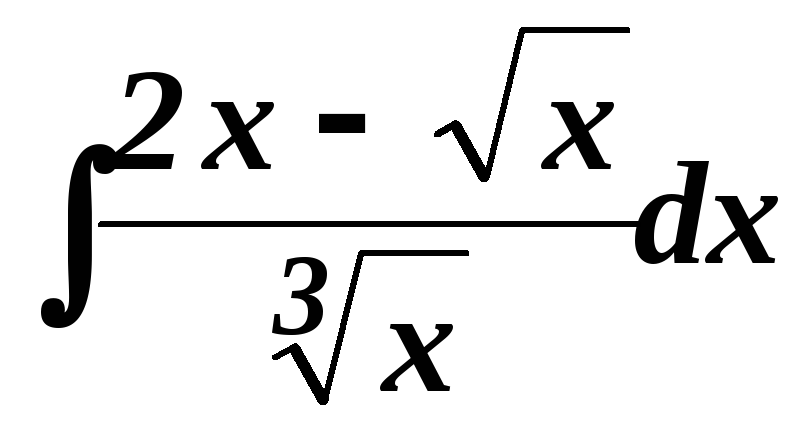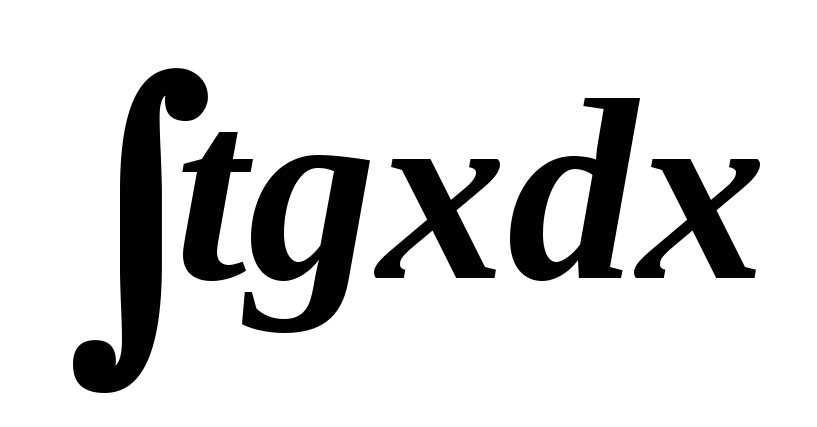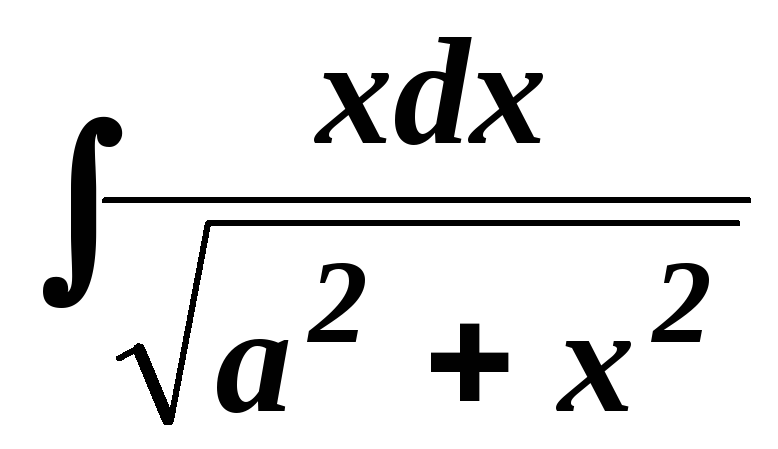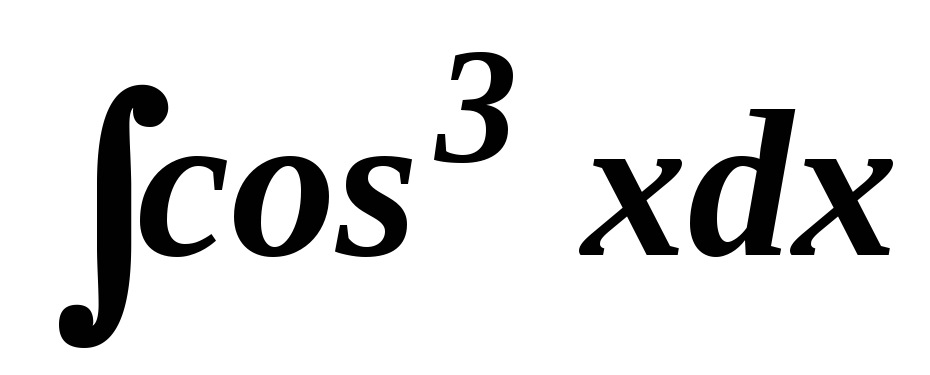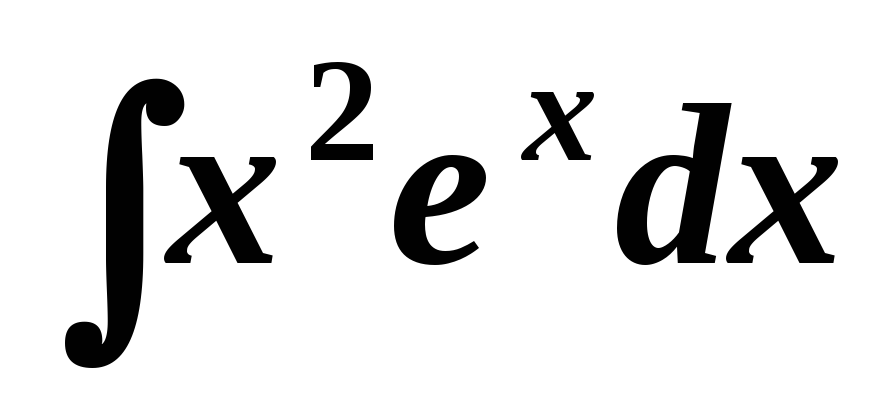5. Самостоятельная работа студентов на занятии.

5.1. Найти интегралы:

1. .

2. .

3. .

4. .

5. .

6. .

7. .

8. .

9. .

10. .

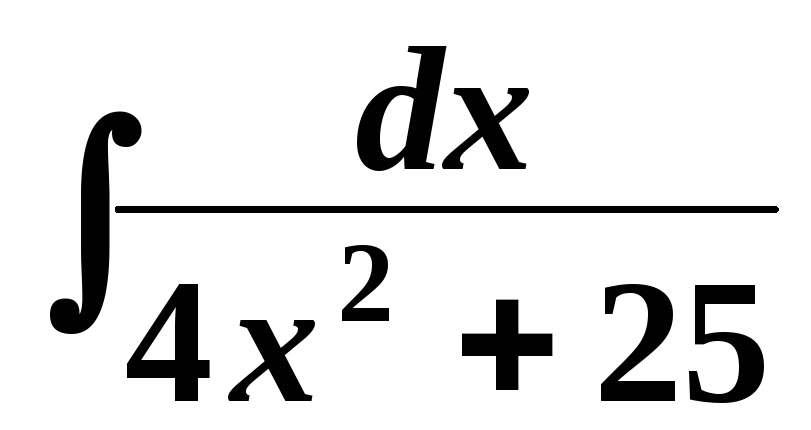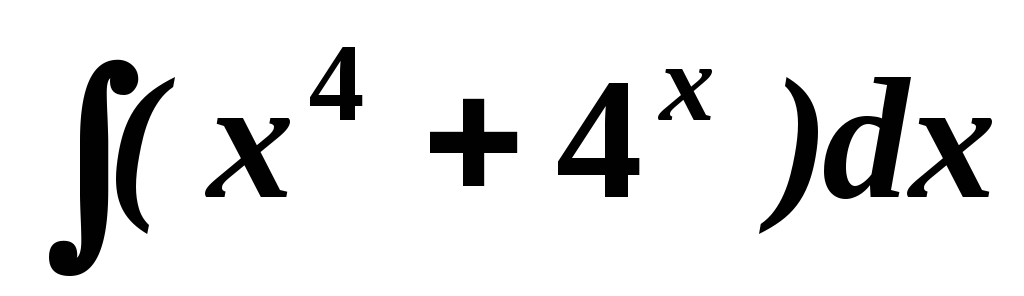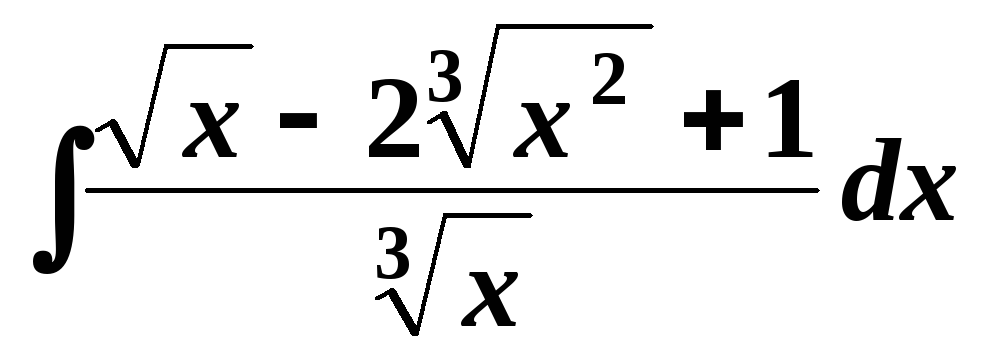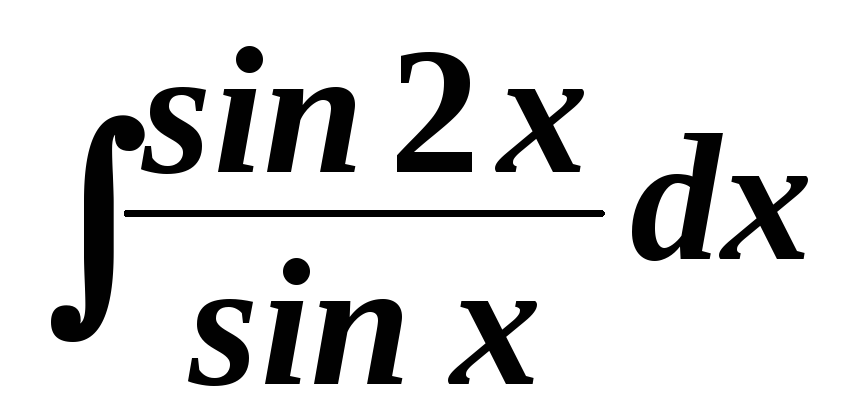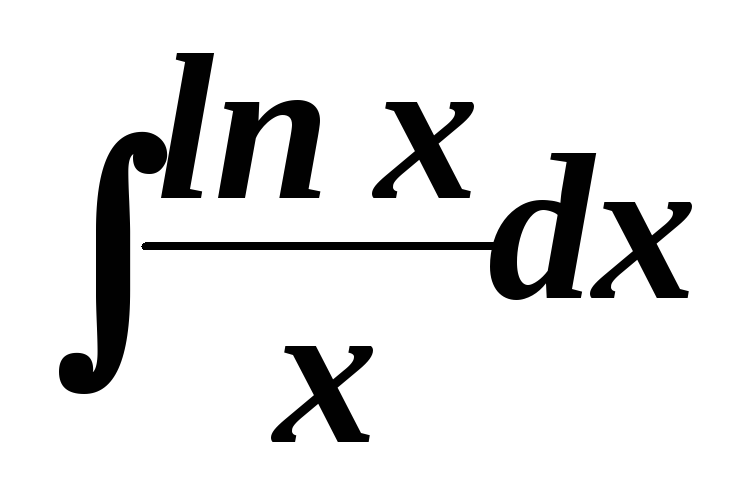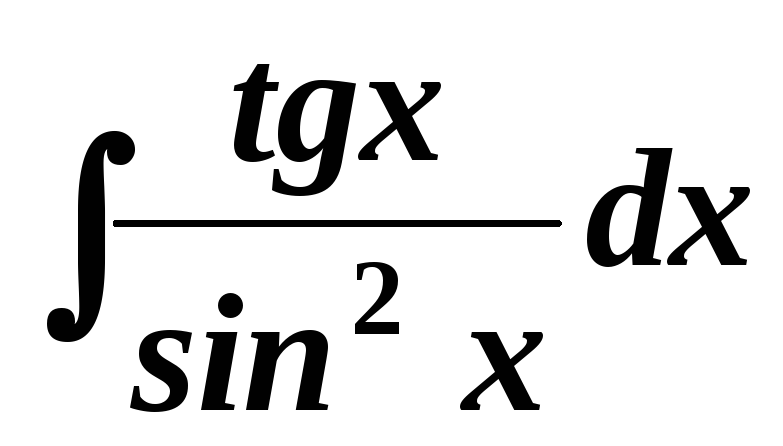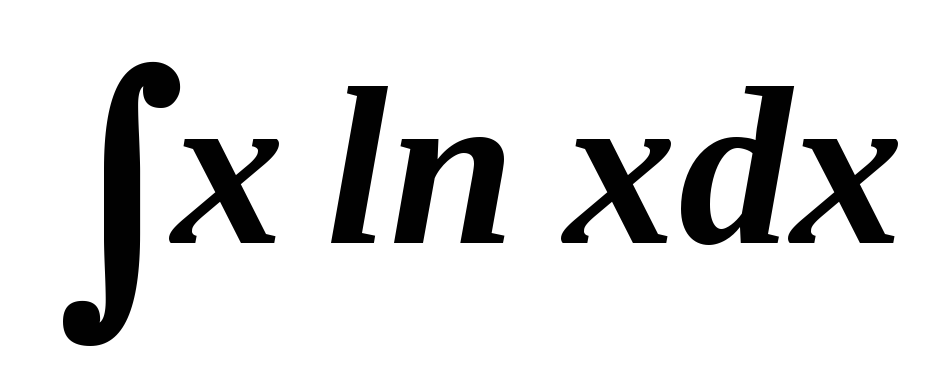6. Задание на дом.

6.1. Практика:

6.1.1. Найти интегралы:

1. .

2. .

3. .

4. .

5. .

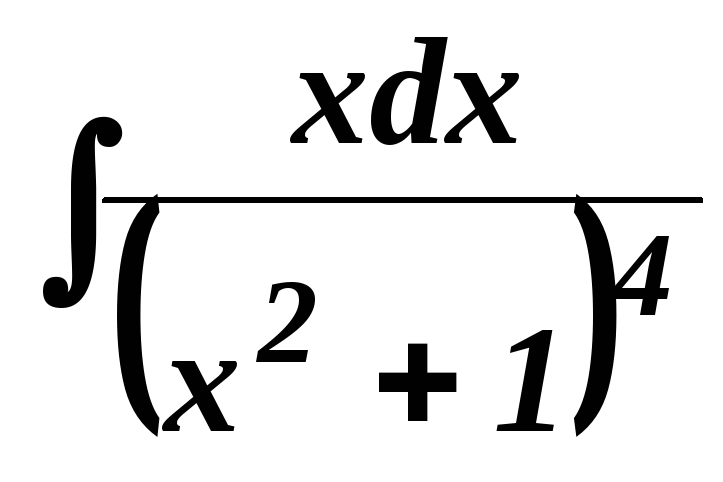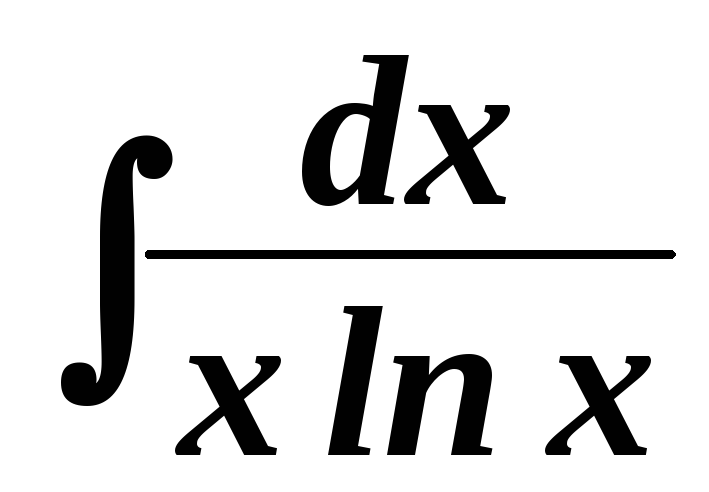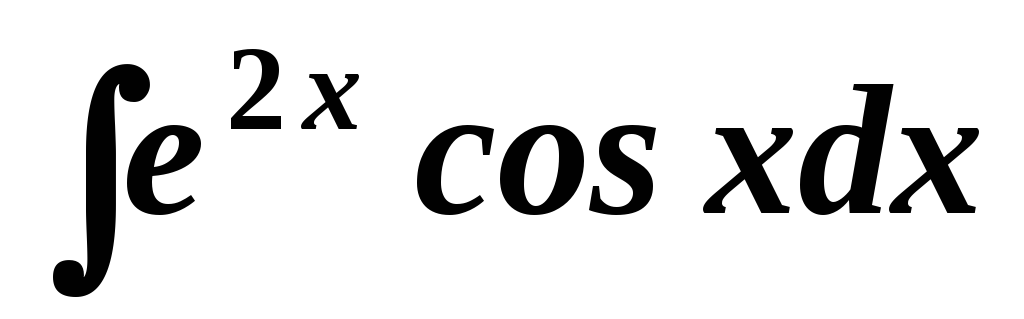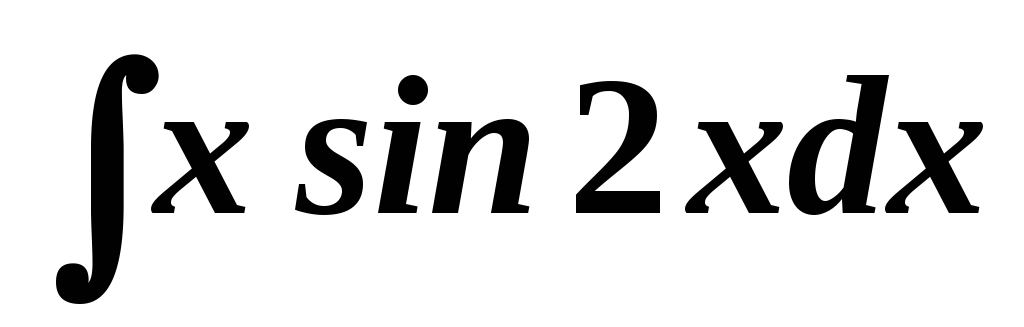6.1.3. Лобоцкая Н.Л. и др. С. 86 № 22,24,38,37.

22. .

24. .

37. .

38. .

6.2. Теория.

6.2.1. Лекция по теме «Определенный интеграл и его основные свойства».

6.2.2. Лобоцкая Н. Л. и др. С. 88-97.

6.2.3. Казуб В.Т. , Воронина С.В. и др. Основы математического анализа. С 96-109.

6.2.4. Казуб В.Т., Воронина С.В. Математический анализ. Дифференциальные уравнения. С. 59-64.

1. Тема: Определенный интеграл и его основные свойства.

2. Актуальность темы: понятие определенного интеграла широко используется в математике и других науках для вычисления площадей плоских фигур, работы переменной силы и т.п.

3. Цель занятия: освоить методы вычисления определенного интеграла.

3.1 Целевые задачи:

знать: понятие определенного интеграла, свойства определенного интеграл, формулу Ньютона-Лейбница, определенный интеграл с переменным верхним пределом;

уметь: вычислять определенный интеграл, пользуясь формулой Ньютона-Лейбница; применять методы интегрирования для вычисления определенного интеграла

4. Краткие сведения из теоретического курса.

Определенный интеграл как предел интегральной суммы

Пусть функция y=f(x) определена на отрезке [a, b], a<b. Выполним следующие действия: разобьем отрезок [a, b] точками а=х₀,х₁…,х_n=b (х₀<х₁<…<х_n) на n частичных отрезков [x₀, x₁], [x₁, x₂],… [x_n-1, x_n]; в каждом частичном отрезке [x_i-1, x_i] возьмем произвольную точку с_i и вычислим f(c_i); умножим f(c_i) на длину соответствующего частичного отрезка x_i=x_i–x_i-1: f(c_i)x_i и составим сумму всех таких произведений. Сумма всех таких произведений называется интегральной суммой функцииy=f(x) на отрезке [a, b]. Найдем предел интегральной суммы, когда n ∞ или maxx_i0.

Если при этом интегральная сумма имеет предел I, который не зависит от способа разбиения отрезка на частичные отрезки, ни от выбора в них, то число I называют определенным интегралом и обозначается .

Таким образом, .

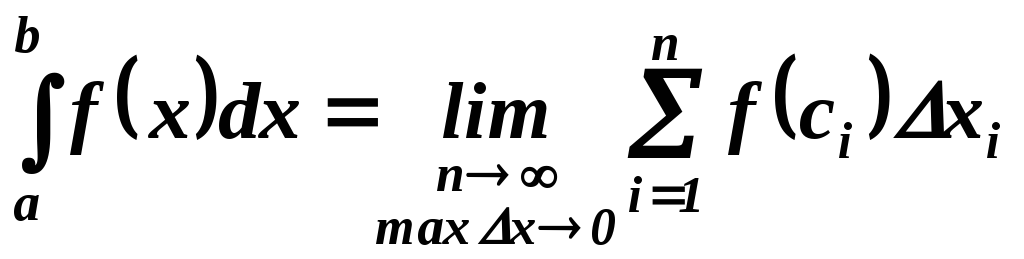Числа а и b называются, соответственно, нижним и верхним пределами интегрирования, f(x) – подынтегральной функцией, х – подынтегральной функцией, отрезок [a, b] – областью (отрезком) интегрирования.

Функция у= f(x), для которой на отрезке [a, b] существует определенный интеграл , называется интегрируемой на этом отрезке.