1. Тема: Приложения определенного интеграла.

2. Актуальность темы: определенный интеграл используется при решении прикладных задач физики, химии, математики и других естественнонаучных задач.

3. Цель занятия: освоить приложения определенного интеграла для вычисления площадей плоских фигур, работы переменной силы; методы приближенного вычисления определенного интеграла.

3.1 Целевые задачи:

знать: понятие определенного интеграла, свойства определенного интеграл, формулу Ньютона-Лейбница, метод трапеций и метод прямоугольников;

уметь: решать задачи на вычисление площадей плоских фигур; вычисление работы переменной силы; находить определенный интеграл с помощью формулы прямоугольников и трапеций.

4. Краткие сведения из теоретического курса.

Задача о площади криволинейной трапеции

Пусть на отрезке [a, b]задана непрерывная функция y=f(x)0. Фигура ограниченная сверху графиком функции, снизу – осью Ох, сбоку – прямыми х=а, х=b, называется криволинейной трапецией.

Площадь криволинейной трапеции, расположенной выше оси абсцисс (f(x)≥0), равна соответствующему определенному интегралу (геометрический смысл определенного интеграла): .Если криволинейная трапеция расположена ниже оси Ох (f(x)<0), то ее площадь может быть найдена по формуле: .

Работа переменной силы

Пусть материальная точка М перемещается вдоль оси Ох под действием переменной силы F=F(x), направленной параллельно этой оси. Работа, произведенная силой при перемещении точки М из положения х=а в положение х=b, находится по формуле: .

Путь пройденный телом

Пусть материальная точка перемещается по прямой с переменной скоростью v=v(t). Путь S, пройденный ею за промежуток времени от t₁ до t₂: .

Приближенное вычисление определенного интеграла. Формула прямоугольников

Пусть на отрезке [a; b], a < b, задана непрерывная функция f(x). Требуется вычислить интеграл . Формула прямоугольников:

.

Формула трапеций

Пусть на отрезке [a; b], a < b, задана непрерывная функция f(x). Требуется вычислить интеграл . Формула трапеций:

или .

Решение задач.

1. Найти площадь плоской фигуры, ограниченной функцией у=sin(x) и осью Ох при условии .

2. Найти площадь фигуры, ограниченной линиями ,.

3. Какую работу нужно затратить, чтобы растянуть пружину на 0,05 м, если сила 100 Н растягивает пружину на 0,01 м?

4. Пусть скорость выражена формулой v(t)=10t+2 (м/с). Найти путь, пройденный телом от начала движения (t=0) до конца 4-й секунды.

5. Вычислить , разбив отрезок интегрирования [1;3] на 4 части.

а) по формуле трапеций:

б) по формуле прямоугольников:

в) найти точное значение интеграла.

5. Самостоятельная работа студентов на занятии

5.1. Вычислить площади фигур ограниченных линиями:

1. у= соs x и осью Ох, в пределах от 0 до.

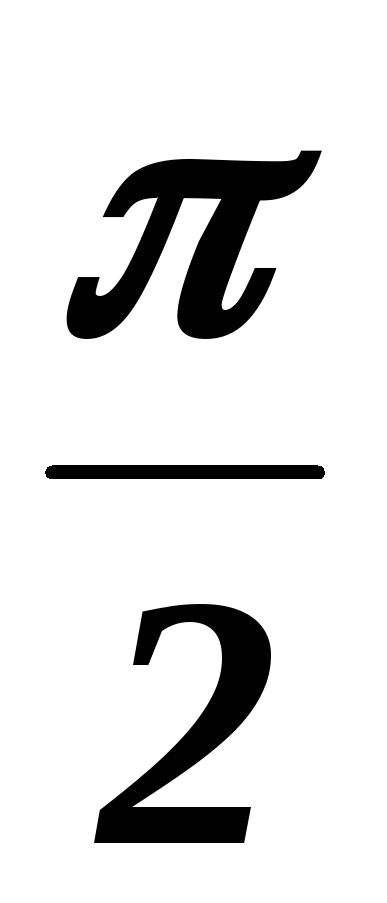2. у=х², у=|х|.

5.2. Вычислить работу, произведенную при сжатии пружины на 0,03 м, если известно, что для укорочения ее на 0,005 м нужно приложить силу в 10 Н .

5.3. Скорость движения тела v=3t²–2t (м/с). Какой путь пройдет тело за 5 с от начала движения?

Задание на дом.

6.1. Практика:

6.1.1. Вычислить площадь фигуры, ограниченной линиями:

1.и;

2.;и.

6.1.3. Лобоцкая Н.Л. и др. С. 105 № 36, 46.

36. Вычислить приближенно по формуле трапеций: при.

46. Определить площадь фигуры, заключенной между кривой и прямой.

6.2. Теория.

6.2.1. Лекция по теме «Дифференциальные уравнения. Дифференциальные уравнения первого порядка».

6.2.2. Лобоцкая Н. Л. и др. С. 107-110.

6.2.3. Казуб В.Т. , Воронина С.В. и др. Основы математического анализа. С 135-137.

6.2.4. Казуб В.Т., Воронина С.В. Математический анализ. Дифференциальные уравнения. С. 81-82, 83-86.