1. Тема: Предел функции.
2. Актуальность темы: Предел функции используется в определении многих математических понятий, например, производной функции одного аргумента, производной функции нескольких переменных, непрерывности функции, определенного интеграла и т. д.
3. Цель занятия: Выработать навыки нахождения пределов функций одной переменной.
3.1 Целевые задачи:
знать: понятия предела функции, понятие бесконечно малой функции, основные теоремы о пределах, первый и второй замечательные пределы;
уметь:
применять основные правила раскрытия
неопределенностей вида (
,
),
применять первый и второй замечательные
пределы при нахождении пределов.
4. Краткие сведения из теоретического курса.
Определение предела функции и бесконечно малой функции
Пусть функция у=f(x) определена в некоторой окрестности точки х0, кроме, может быть, самой точки х0.
Число А
называется
пределом функции в точке х0
(или при
х
х0),
если для любого положительного
найдется такое положительное число ,
что для всех хх0,
удовлетворяющих неравенству
,
выполняется неравенство
.
Записывается это
так:
.
Функция y=f(x)
называется бесконечно малой при х
х0,
если
.
Можно дать другое определение: для любого >0 найдется такое >0, что для всех хх0, удовлетворяющих неравенству 0<х - х0 , выполняется неравенство f(x).
Обозначают бесконечно малые функции греческими буквами или хх и т. д.
Теорема о связи бесконечно малой функции и предела
Теорема. Если функция f(x) при х х0 имеет предел, равный числу А, то она может быть представлена в виде f(x)= A + (x), где (x) – бесконечно малая.
Справедливо и
обратное утверждение:
Если функцию f(x)
можно представить в виде суммы числа
А
и бесконечно малой функции
,то число А
является пределом функции
f(x)
при х
х0.
Основные теоремы о пределах
Теорема 1.
Предел
постоянной равен самой постоянной:
Теорема 2. Предел алгебраической суммы двух функций равен сумме их пределов при условии, что эти пределы существуют:
Теорема 3. Предел произведения двух функций равен произведению пределов, если последние существуют:
Следствие 1.
Постоянный
множитель может быть вынесен за знак
предела:
Следствие 2.
Предел
степени с натуральным показателем
равен той же степени предела:
Теорема 4. Предел отношения двух функций равен отношению их пределов, если последние существуют, и предел делителя отличен от нуля:
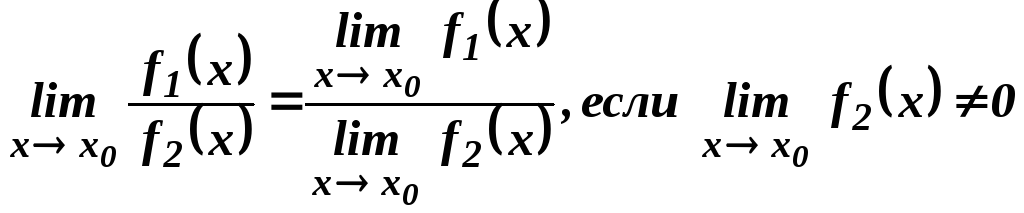
Теорема 5.
Если функция заключена между двумя
функциями j(x)
и g(x),
имеющими общий предел, то функция f(x),
имеет тот же предел, т. е. если
и
,
то
.
Первый и второй замечательный пределы
Первый замечательный предел
Предел отношения
синуса угла к углу при стремлении угла
к нулю равен единице:
Второй замечательный предел. Число e
Выражение
для целочисленныхn®¥
имеет свои пределом иррациональное
число e
= 2,7182818284590452353… то есть
.
Этот предел называютвторым
замечательным пределом.
Можно доказать, что к числу е
стремится
и предел функции
:
,
где хR.
В рассмотренном
выше пределе произведем замену:
,
тогда если
,
то
и получим
.
Второй замечательный предел имеет широкое применение. С его помощью находят многие другие пределы.
Рис. 1.1
Во многих
естественнонаучных задачах широко
используется логарифм с основанием е,
который носит название натурального
или неперова
и обозначается:
.
График функции
получил
названиеэкспоненты
(рис. 1.1).
Решение задач
Вычислить пределы:
;
.
.
.
.
.
.
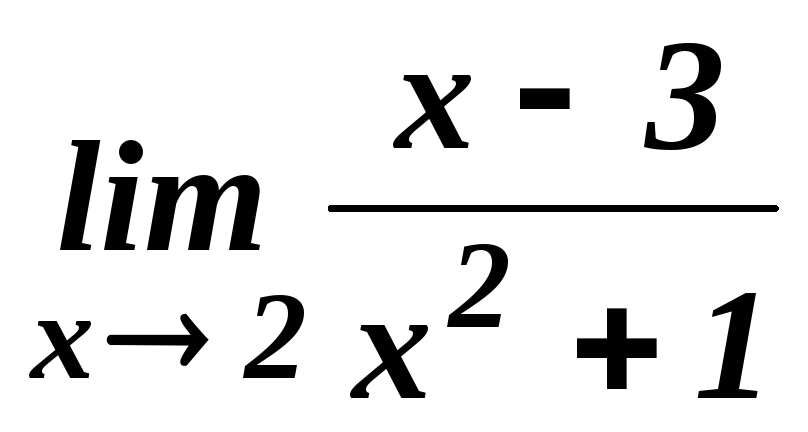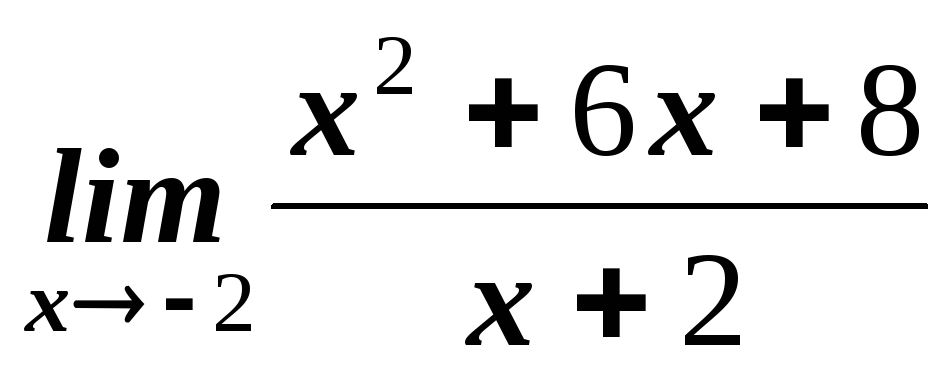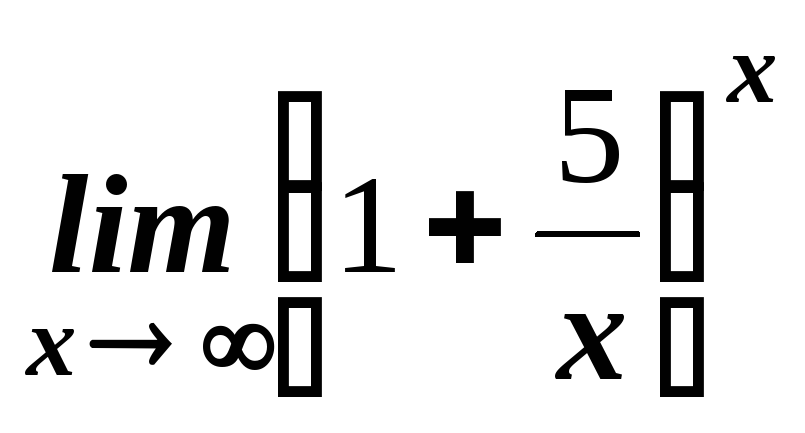5. Самостоятельная работа студентов на занятии.
5.1. Найти пределы функций:
.
.
.
.
.
.
.
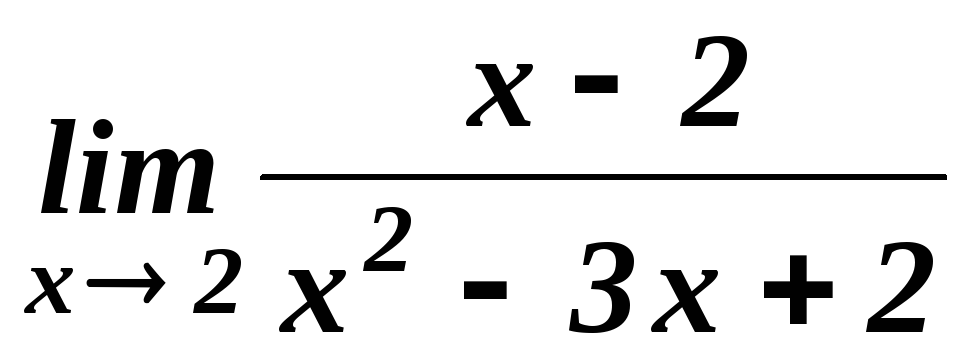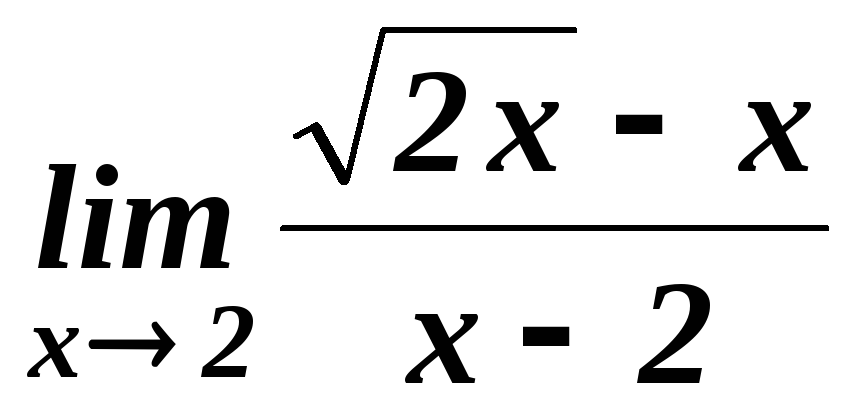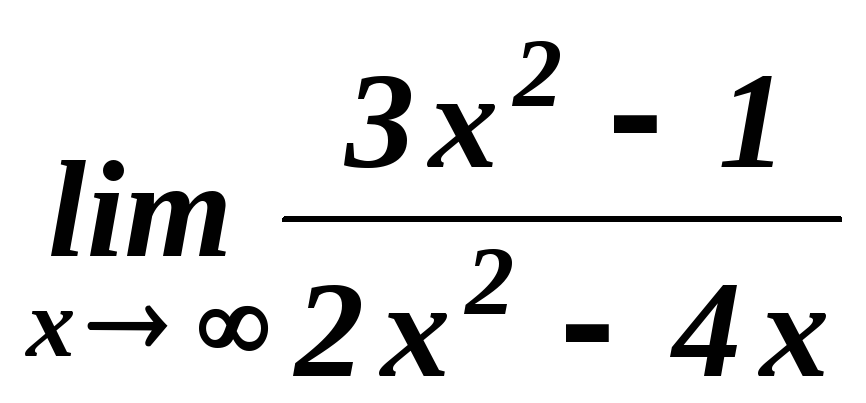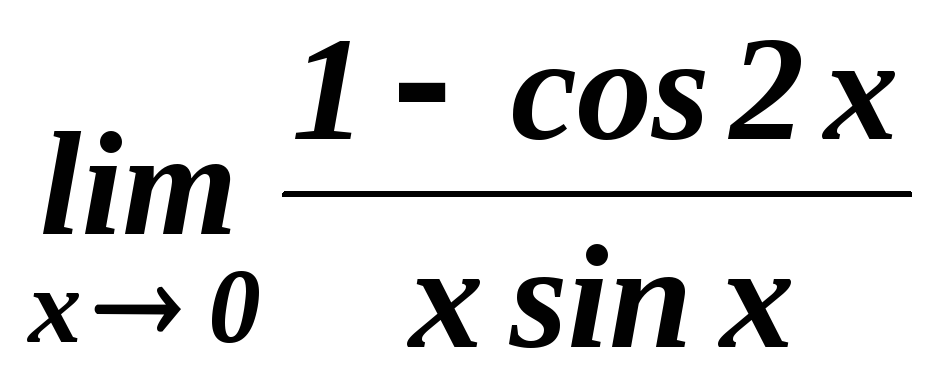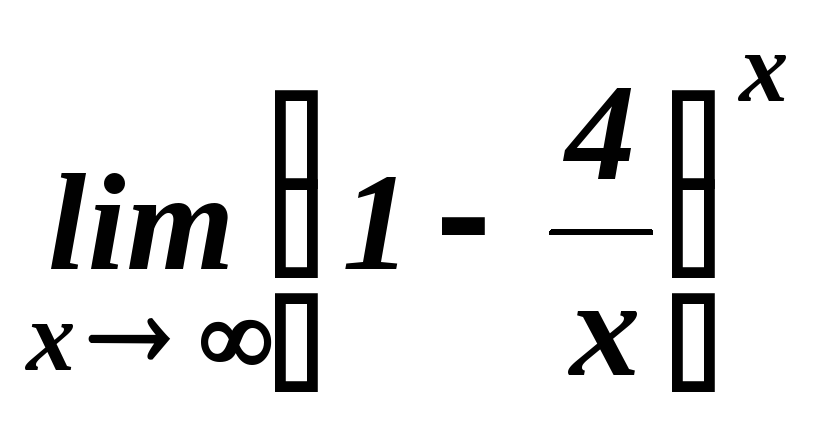6. Задание на дом:
6.1. Практика:
6.1.1. Найти пределы функций:
.
.
.
.
.
.
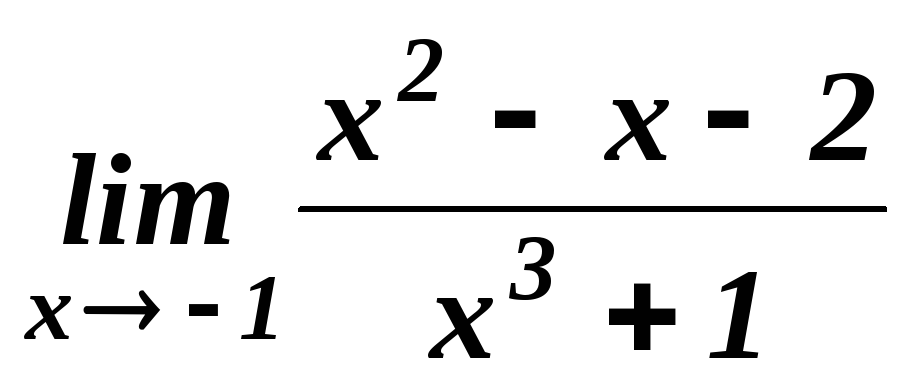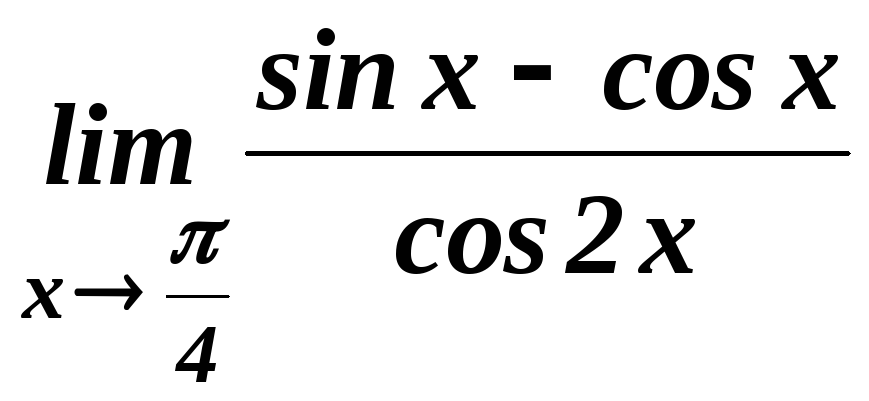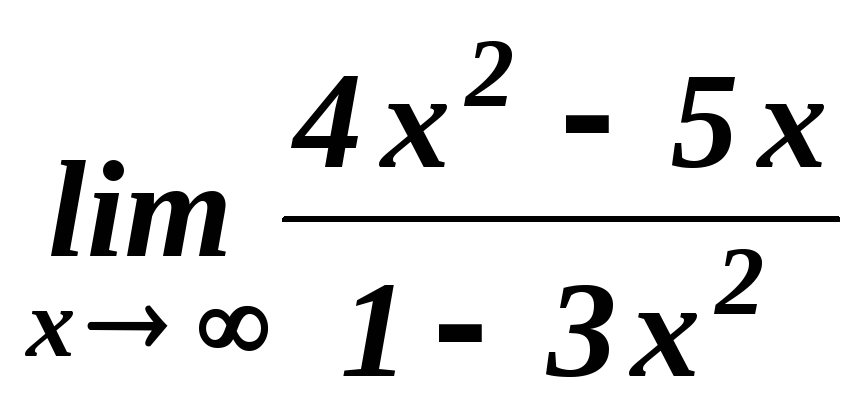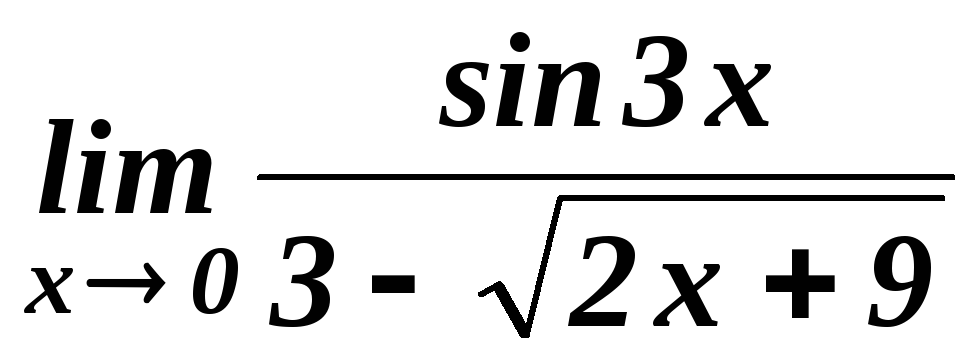6.1.2. Лобоцкая Н.Л. и др. С. 28, №№ 30,32,38,42, 54.
30.
.
32.
.
38.
.
42.
54.
.
6.2. Теория:
6.2.1. Лекция по теме «Производная функции».
6.2.2. Лобоцкая Н. Л. и др. С. 30-45.
6.2.3. Казуб В.Т. , Воронина С.В. и др. Основы математического анализа. С 63-69.
6.2.4. Казуб В.Т., Воронина С.В. Математический анализ. Дифференциальные уравнения. С. 27-31