
- •Математика и информатика
- •1. Тема: Предел функции. 3
- •1. Тема: Предел функции.
- •Второй замечательный предел. Число e
- •1. Тема: Производная функции.
- •4. Краткие сведения из теоретического курса
- •1. Тема: Дифференциал функции.
- •4. Основные сведения из теоретического курса
- •1. Тема: Производные и дифференциалы высших порядков
- •6. Задание на дом.
- •6.1. Практика:
- •1. Тема: Применение производных к исследованию функций
- •4. Основные сведения из теоретического курса
- •1. Тема: Производные и дифференциалы функции нескольких аргументов. Приложение полного дифференциала функции
- •Частные производные второго порядка
- •5. Самостоятельная работа студентов на занятии.
- •1. Тема: Неопределенный интеграл и его основные свойства. Основные методы интегрирования.
- •Основные понятия
- •Свойства неопределенного интеграла
- •Метод непосредственного интегрирования
- •Свойство инвариантности неопределенного интеграл
- •Метод замены переменной (подстановки)
- •6. Задание на дом.
- •1. Тема: Определенный интеграл и его основные свойства.
- •Свойства определенного интеграла
- •Геометрический смысл определенного интеграла
- •Формула Ньютона-Лейбница
- •Метод замены переменных в определенном интеграле
- •1. Тема: Приложения определенного интеграла.
- •Задача о площади криволинейной трапеции
- •Работа переменной силы
- •Приближенное вычисление определенного интеграла. Формула прямоугольников
- •5. Самостоятельная работа студентов на занятии
- •1. Тема: Обыкновенные дифференциальные уравнения. Дифференциальные уравнения первого порядка с разделяющимися переменными. Однородные дифференциальные уравнения первого порядка
- •Дифференциальные уравнения с разделяющимися переменными
- •5. Самостоятельная работа студентов на занятии
- •1. Тема: Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами и их решение
- •5. Самостоятельная работа студентов на занятии
- •1. Тема: Применение дифференциальных уравнений для решения прикладных задач
- •5. Самостоятельная работа студентов на занятии
- •6. Задание на дом.
- •1. Тема: Знакомство с персональным компьютером. Основные приемы работы с операционной системой Windows
- •1. Оперативное запоминающее устройство (оперативная память)
- •2. Быстродействие эвм
- •3. Характеристики внешней памяти (внешнее запоминающее устройство - взу)
- •4. Характеристики монитора
- •5. Тип интерфейса и возможности расширения конфигурации технических средств
- •Периферийные устройства
- •5. Самостоятельная работа студентов на занятии
- •1. Тема: Контрольная работа
- •1. Тема: Работа с программой графической обработки данных.
- •4. Краткие сведения из теоретического курса
- •Базовое (системное) и прикладное программное обеспечение
- •6. Задание на дом
- •1. Тема: Работа с текстовым редактором ms Word.
- •4. Краткие сведения из теоретического курса
- •5. Самостоятельная работа студентов на занятии
- •1. Тема: Работа с электронными таблицами. Ms Excel.
- •4. Краткие сведения из теоретического курса
- •5. Самостоятельная работа студентов на занятии
- •1. Тема: Базы данных. Компьютерные сети.
- •4. Краткие сведения из теоретического курса
- •Компьютерные сети
- •Интернет
- •Электронная почта
- •Протокол ftp
- •Www (World Wide Web) – всемирная путина
- •5. Самостоятельная работа студентов на занятии
- •Библиографический список
- •Математика и информатика
- •Часть I
1. Тема: Производная функции.
2. Актуальность темы: Понятие производной является одним из основных математических понятий. Производная широко используется при изучении скорости разных процессов
3. Цель занятия: Выработать навыки нахождения производных функций одной переменной, производных сложных функций.
3.1 Целевые задачи:
знать: понятия приращения аргумента и функции, понятие производной функции, ее геометрический и механический смысл, производную сложной функции, основные правила дифференцирования и таблицу производных;
уметь: применять основные правила дифференцирования и таблицу производных при решении примеров, находить производные сложных функций.
4. Краткие сведения из теоретического курса
Пусть функция y=f(x) определена на некотором интервале. Приращением аргумента называется разность между двумя значениями аргумента Δх= х - х0. Разность между двумя значениями функции называется приращением функции: Δy= Δf = f(x0-x)-f(x0)
Задача о скорости движения точки.
Пусть
материальная точка
М
движется
неравномерно по некоторой прямой.
Каждому значению времени
t
соответствует
определенное расстояние, которое
зависит от истекшего времени
t,
т.е.
S=S(t).
Это
равенство называют законом движения
точки. Найдем скорость движения точки.
Если в некоторый момент времени
t
путь
равен
S,
то
в момент времени
t +
Δt (Δt
–
приращение
времени)
S+S,
за
промежуток времени
t
путь
изменился на величину
ΔS.
Предел
средней скорости
![]() движения
при стремлении к нулю промежутка
времени Δt
называется
скоростью движения точки в данный
момент
времени
(или мгновенной скоростью). Обозначив
эту скорость через V,
получим
движения
при стремлении к нулю промежутка
времени Δt
называется
скоростью движения точки в данный
момент
времени
(или мгновенной скоростью). Обозначив
эту скорость через V,
получим
![]() .
.
Задача о касательной к кривой
Рассмотрим
график непрерывной кривой у
= f(x),
имеющий в точке М(х;у)
невертикальную касательную (рис. 2.1).
Найдем ее угловой коэффициент
k = tgα,
где α
– угол касательной с осью
Ох.
Для этого проведем через точку М
и точку
М1
графика с абсциссой x+Δx
секущую. Обозначим через у
–
угол между секущей MM1
и осью Ох.
Угловой коэффициент секущей равен
![]() .
.
 Рис.
2.1.
Рис.
2.1.
При
Δx→0
Δу
тоже стремиться к нулю, поэтому точка
М1
неограниченно приближается по кривой
к точке М,
а секущая ММ1,
поворачиваясь около точки М,
переходит в касательную. Угол φ→α,
т. е.
![]() .
Поэтому угловой коэффициент касательной
равен
.
Поэтому угловой коэффициент касательной
равен
![]()
Определение.
Если функция
f
(x)
определенная на промежутке (a;
b),
то производной функции f(x)
в точке
![]() называется предел отношения приращения
функции
называется предел отношения приращения
функции![]() к приращению независимого переменного
к приращению независимого переменного![]() приDx,
стремящемся к нулю
приDx,
стремящемся к нулю
![]() .
.
Производная сложной функции
Теорема (о
производной сложной функции): Если
функция
![]() имеет производную
имеет производную![]() в точкех, а функция
в точкех, а функция
![]() – производную
– производную![]() в соответствующей точкеи,
то сложная функция
в соответствующей точкеи,
то сложная функция
![]() в данной точкеx
имеет производную
в данной точкеx
имеет производную
![]() ,
которая находится по формуле
,
которая находится по формуле
![]() .
.
Таблица основных формул дифференцирования
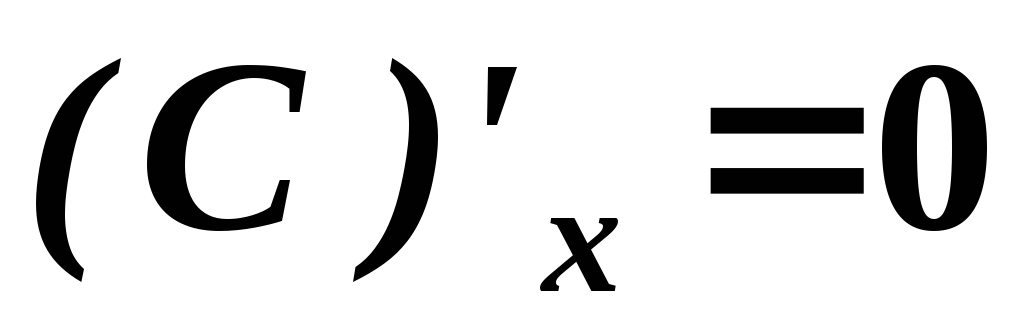 .
.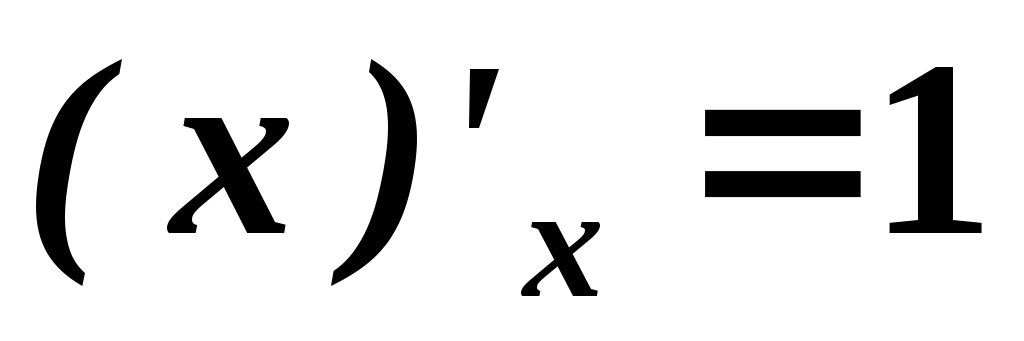 .
.
 .
.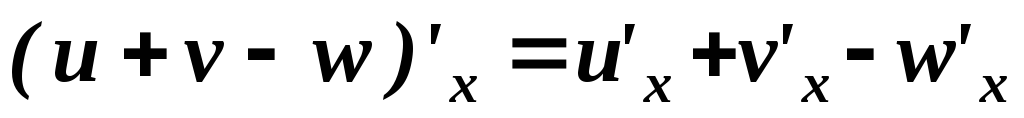 .
. .
.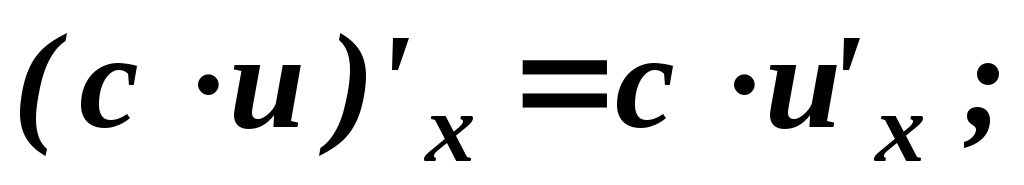
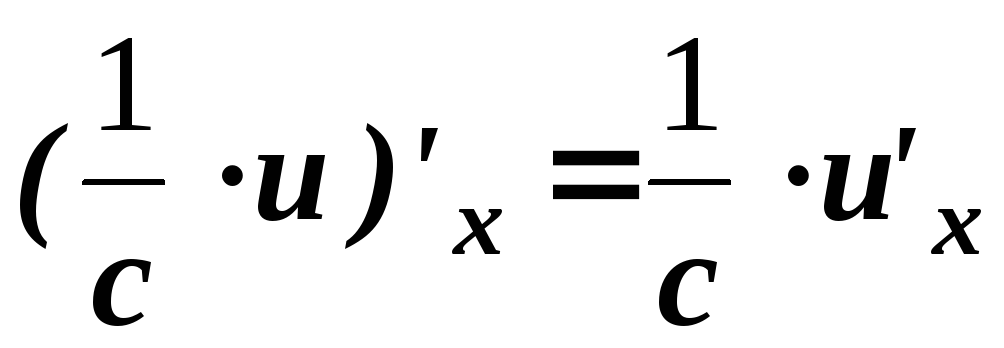 .
.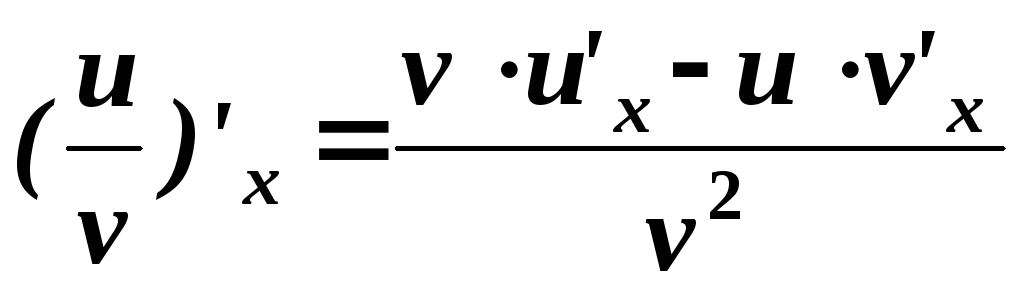 .
. ;
;
 .
.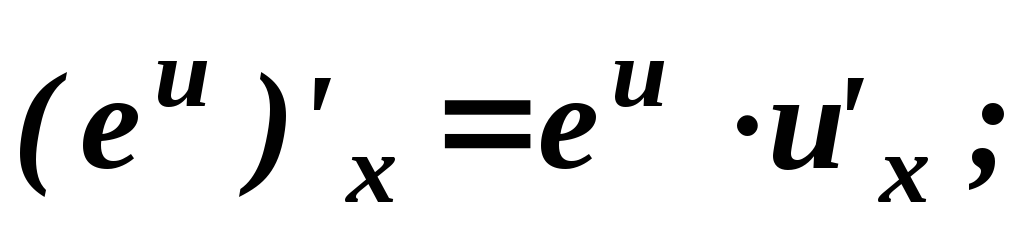
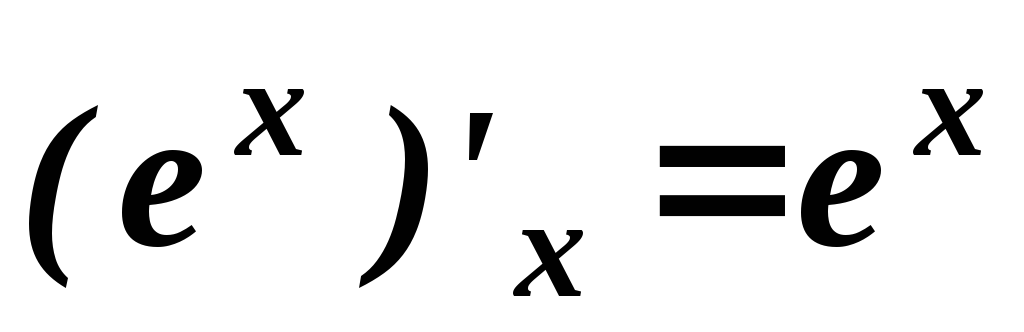 .
.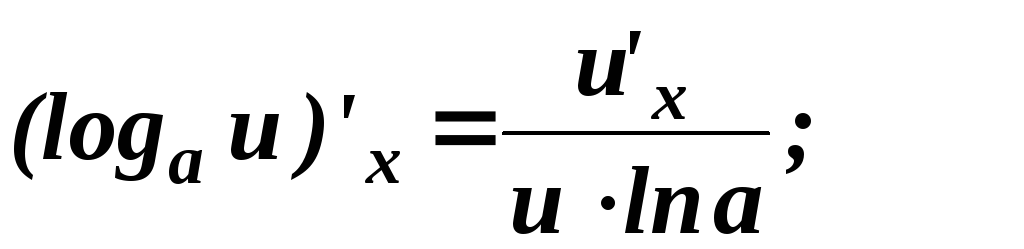
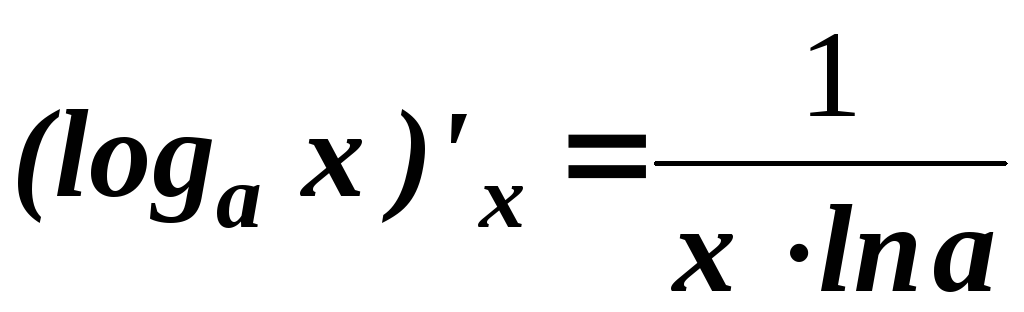 .
.
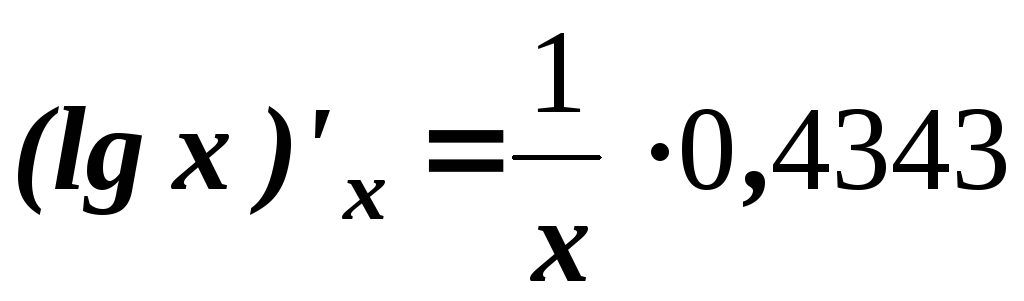 .
.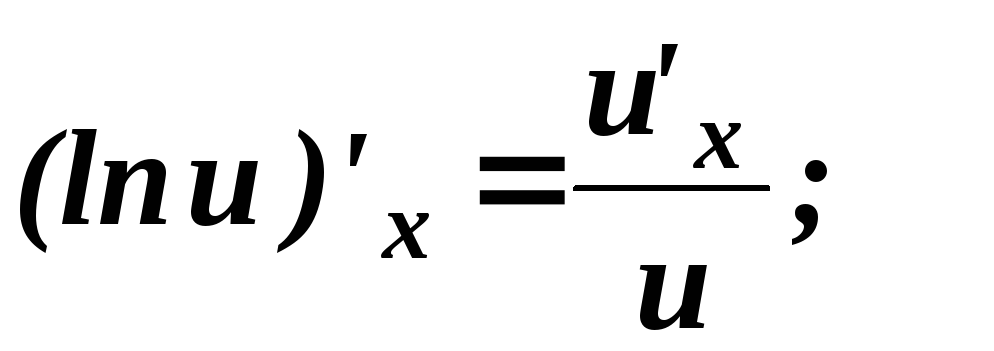
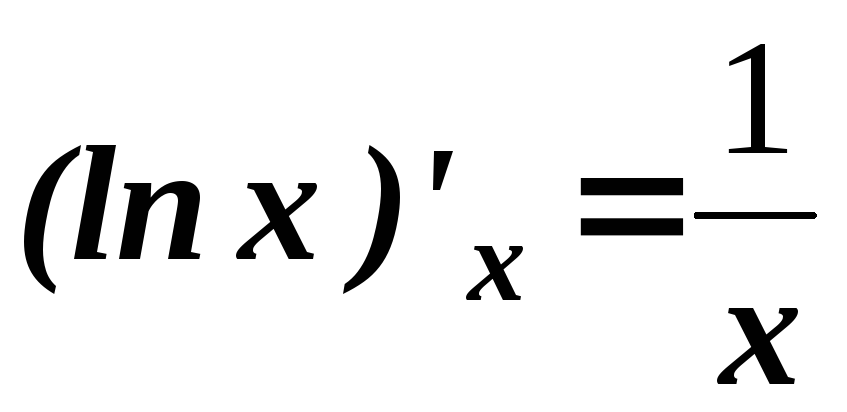 .
.
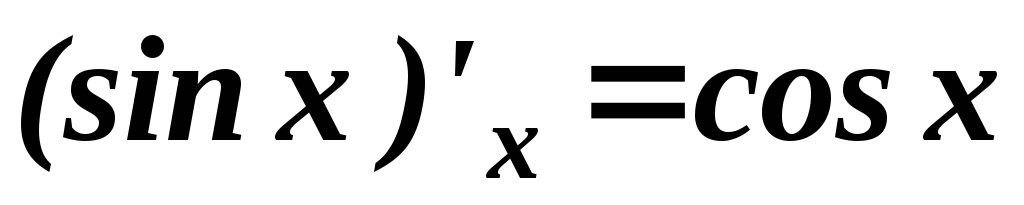 .
.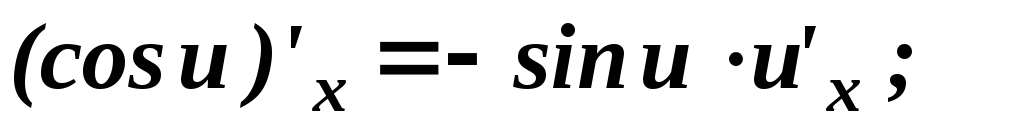
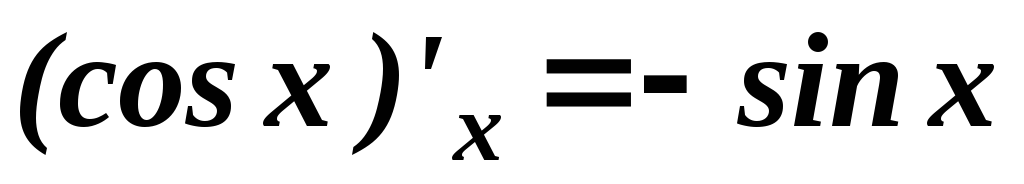 .
.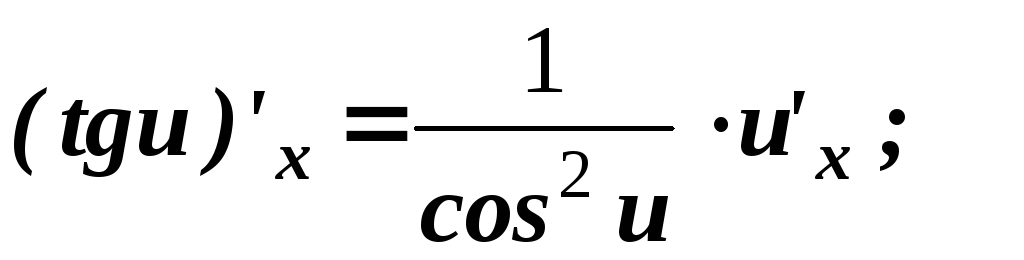
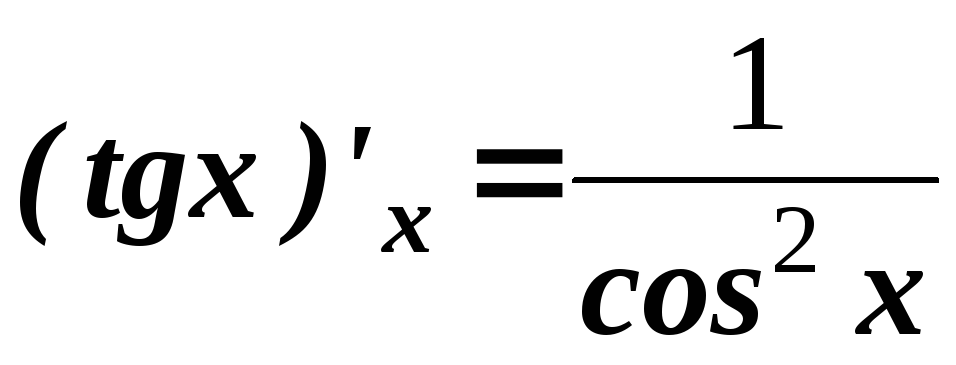 .
.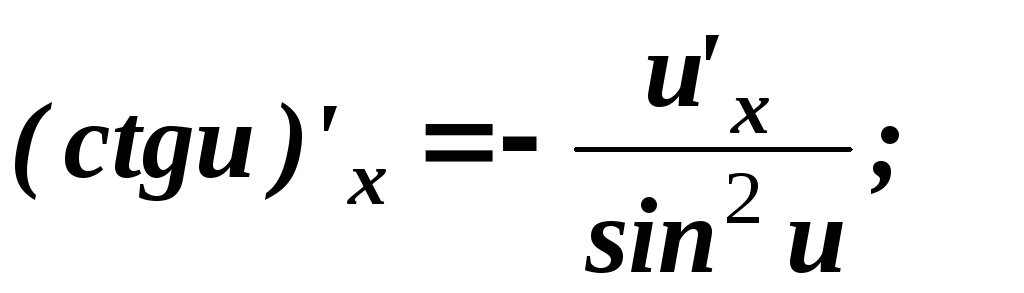
 .
.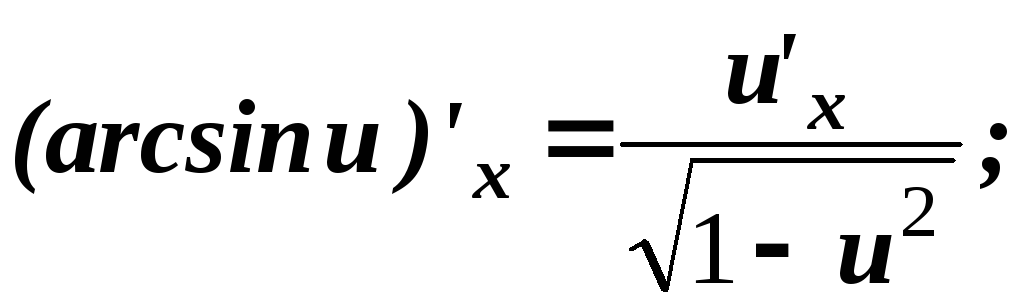

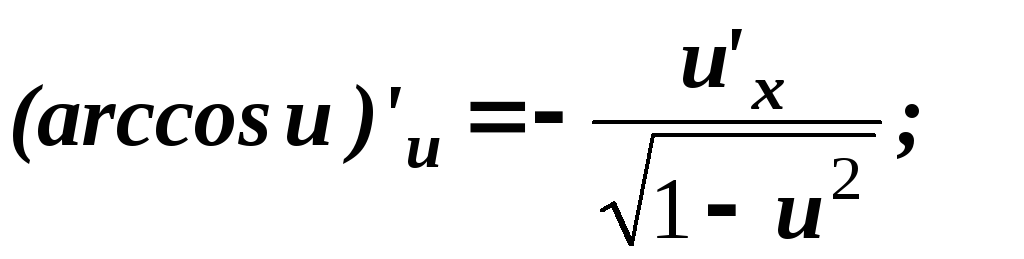
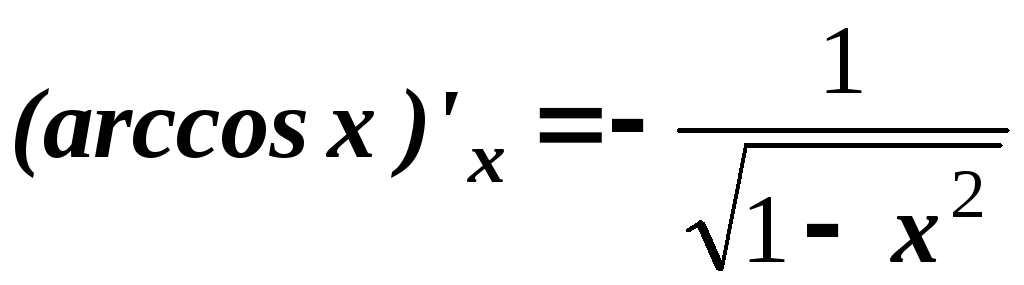 .
.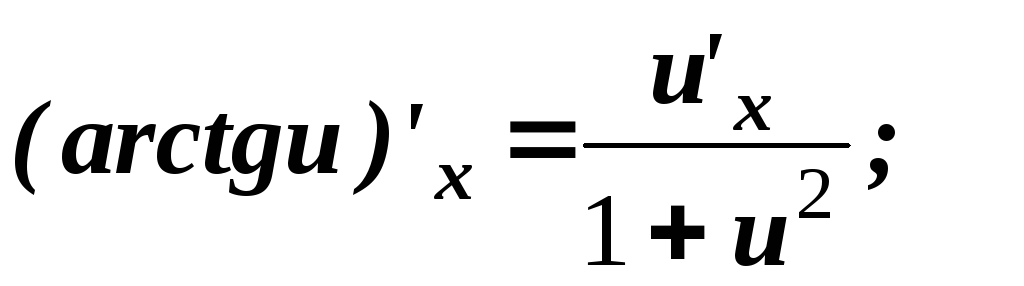
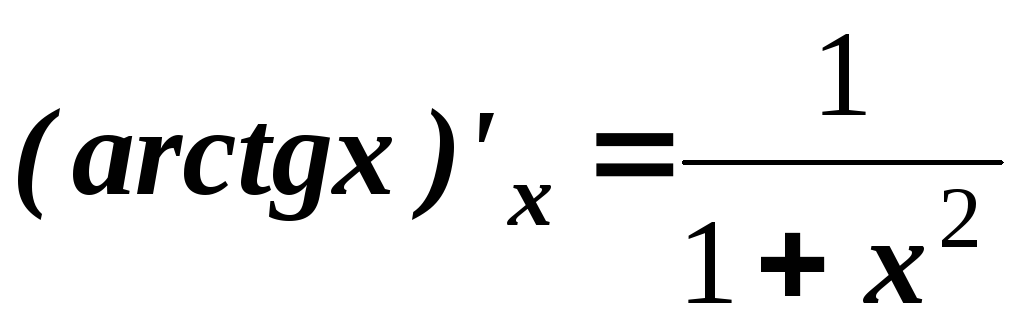 .
.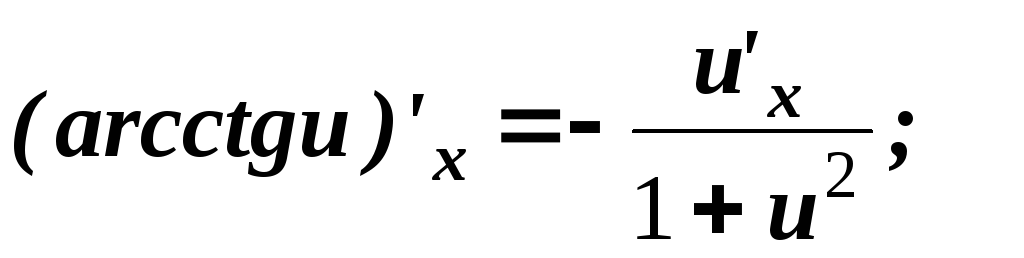
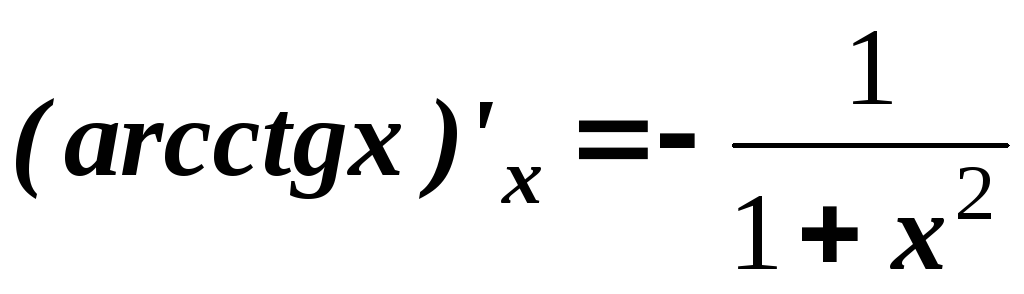 .
.
Решение задач.
Найти производные функций:
 .
.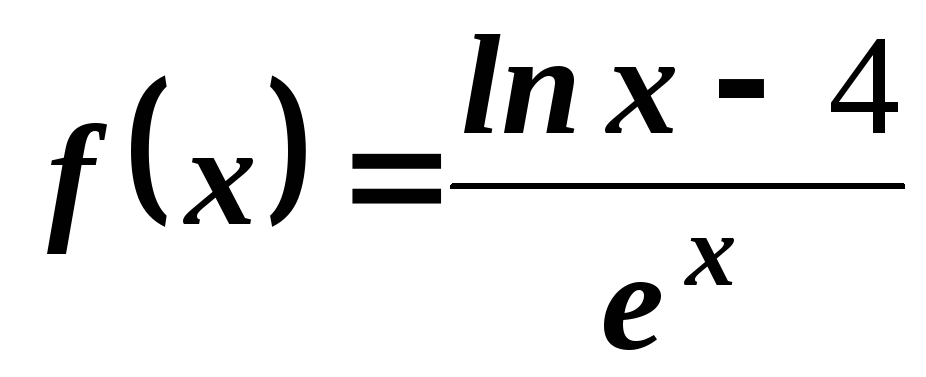 .
.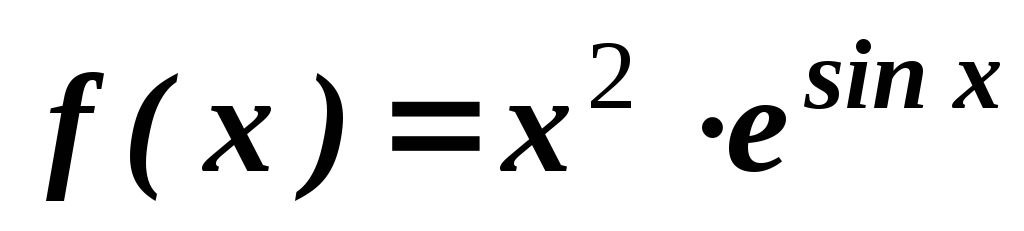 .
.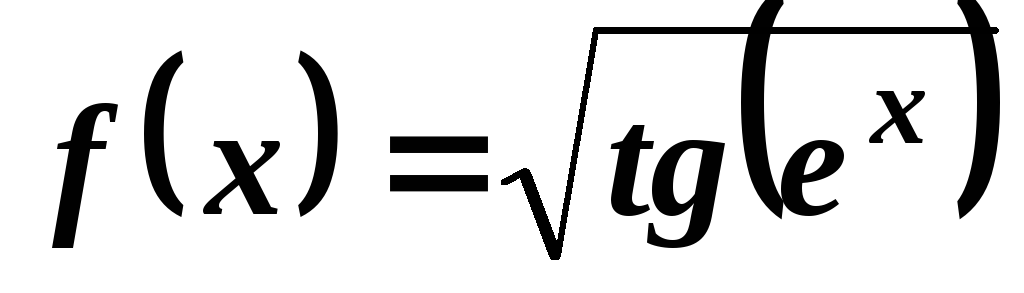 .
.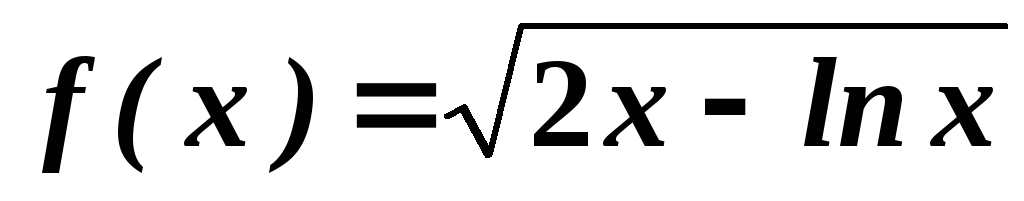 .
.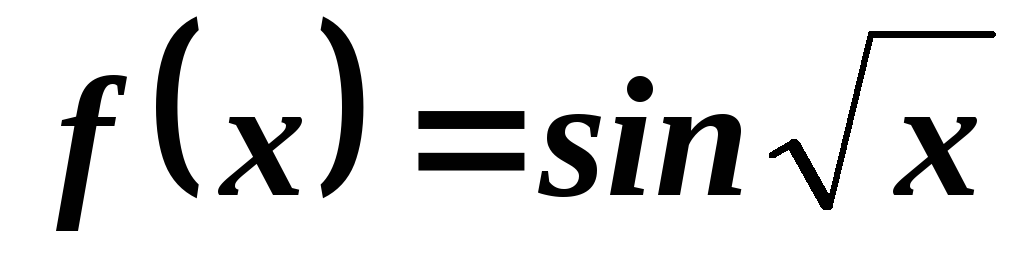
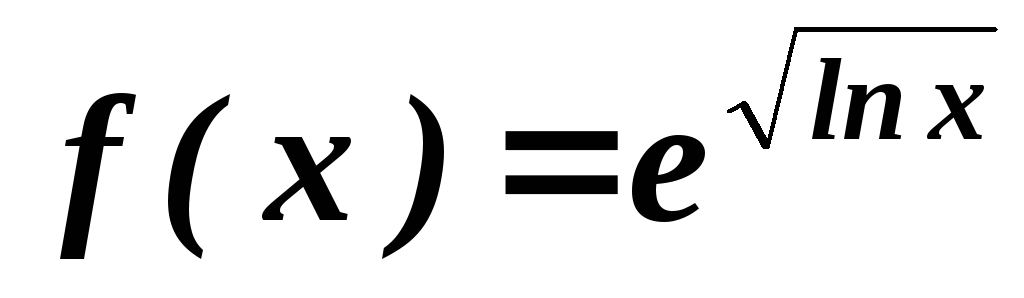 .
.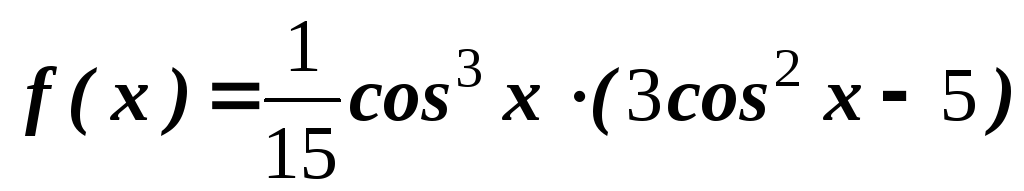
 .
.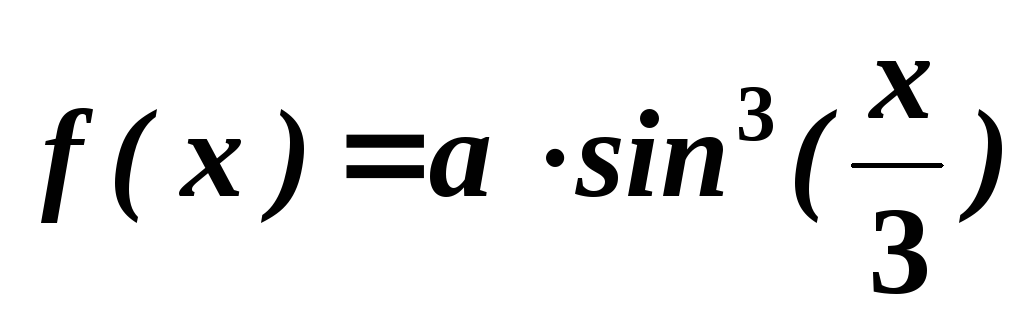 .
. .
.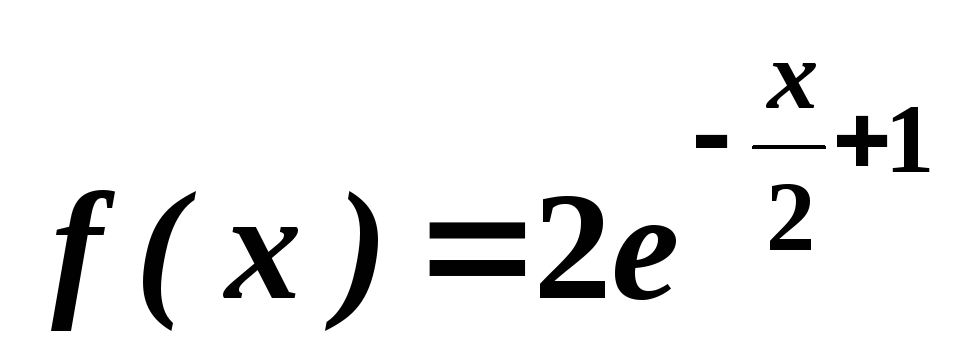 .
.
5. Самостоятельная работа студентов на занятии.
Найти производные функций:
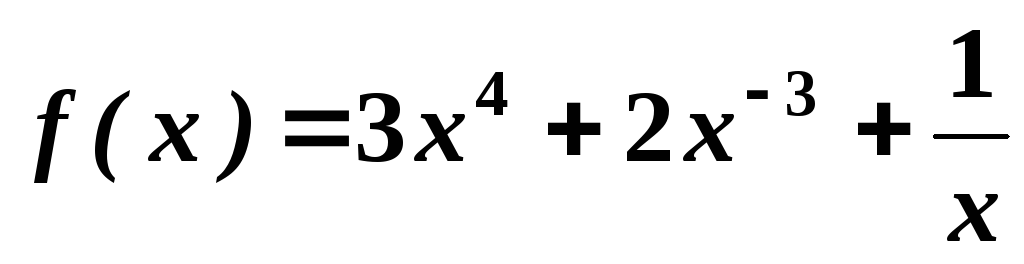 .
.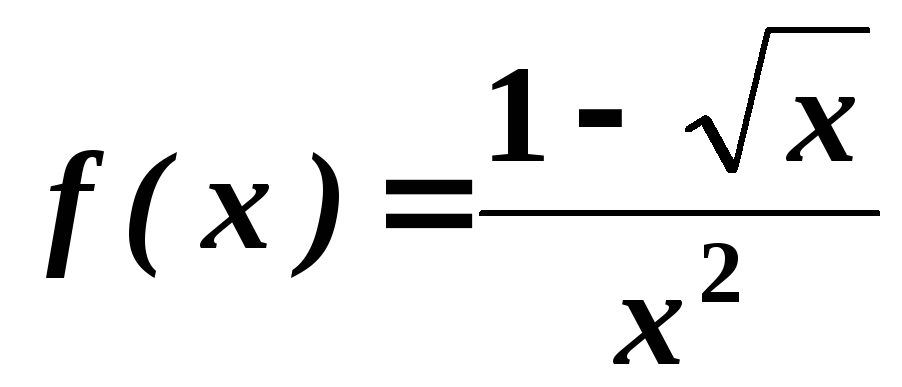 .
.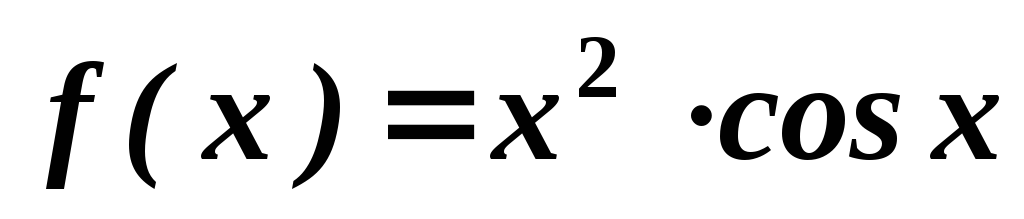 .
.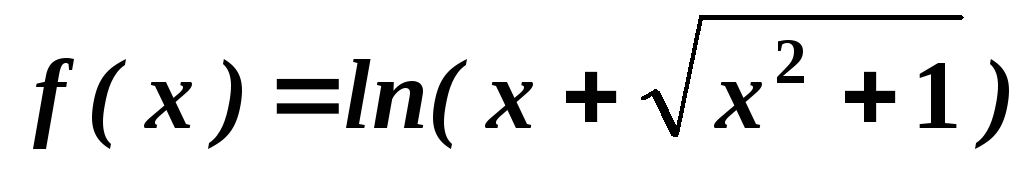 .
. .
.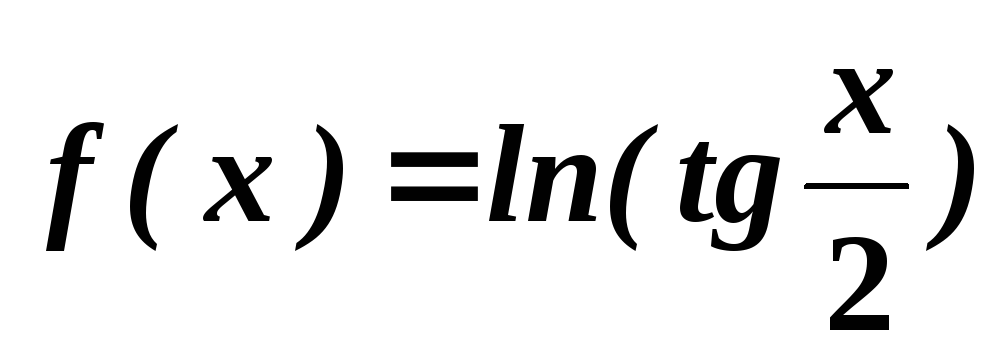 .
.
6. Задание на дом:
6.1. Практика:
6.1.1. Найти производные функций:
 .
.
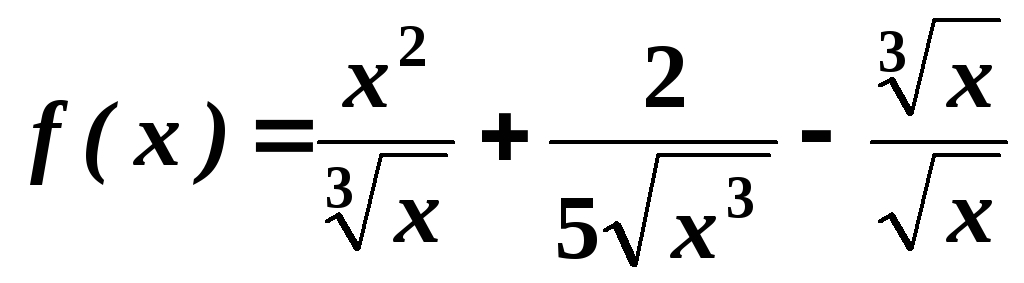 .
.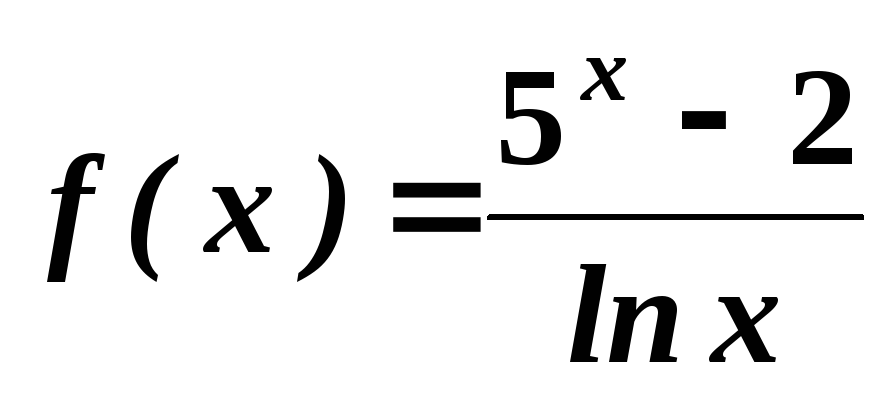 .
. .
.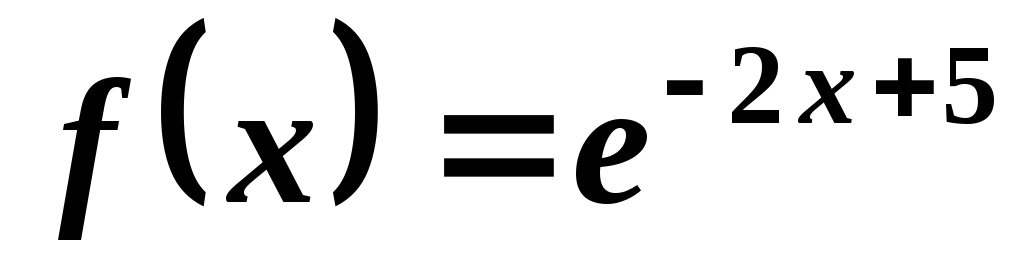 .
. .
.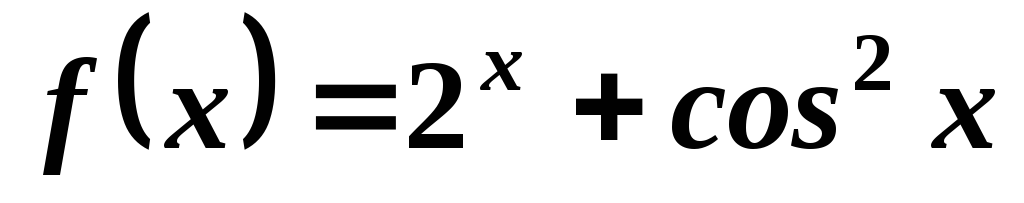 .
.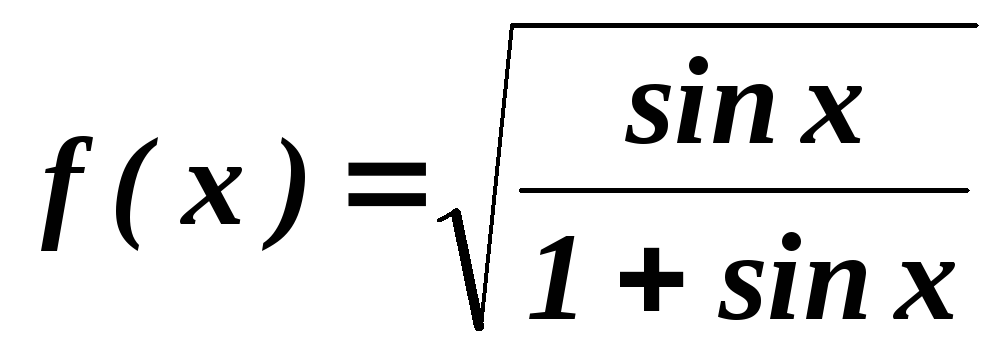 .
.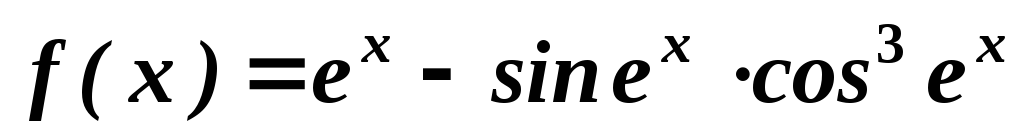 .
.
6.1.2. Лобоцкая Н.Л. и др. С. 55, №№ 40, 44, 54, 56-60.
40.
![]() .
.
44.
![]() .
.
54.
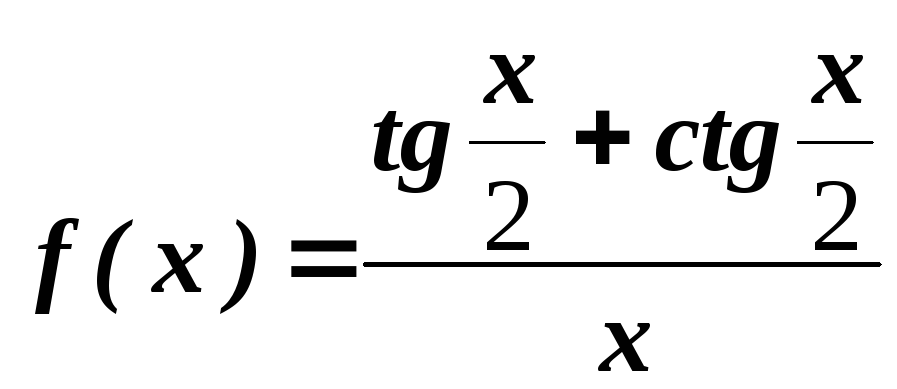 .
.
56.
![]() .
.
57.
![]() .
.
58.
![]() .
.
59.
![]() .
.
60.
![]() .
.
6.2. Теория:
6.2.1. Лекция по теме «Дифференциал функции».
6.2.2. Лобоцкая Н. Л. и др. С. 47-49.
