1. Тема: Производные и дифференциалы функции нескольких аргументов. Приложение полного дифференциала функции

2. Актуальность темы: данный раздел математики имеет широкое применение при решении ряда прикладных задач, так как многим явлениям физического, биологического, химического явления присуща зависимость не от одной, а от нескольких переменных (факторов).

3. Цель занятия: научиться находить производные и дифференциалы функций нескольких переменных; применять полный дифференциал функции при решении прикладных задач.

3.1 Целевые задачи:

знать: понятие функции двух переменных; понятие частных производных функции двух переменных; понятие полного и частных дифференциалов функции нескольких переменных;

уметь: находить производные и дифференциалы функций нескольких переменных; применять полный дифференциал функции при нахождении приближенных значений функции.

4. Краткие сведения из теоретического курса

Переменная z называется функцией двух аргументов x и y, если некоторым парам значений по какому-либо правилу или закону ставится в соответствие определенное значениеz. Функция двух аргументов обозначается .

Функция задается в виде поверхности в прямоугольной системе координат в пространстве. Графиком функции двух переменныхназывается множество точек трехмерного пространства(x, y, z), аппликата z которых связана с абсциссой х и ординатой у функциональным соотношением .

Рассмотрим функцию z=f(x,y). Дадим аргументу х приращение х, а аргументу у – приращение у. Тогда функция z получит наращенное значение .

Величина называется полным приращением функции в точке. Частным приращением по переменнойх называется величина: . Аналогично определяется частное приращение по переменнойу: .

Частные производные и дифференциалы функции нескольких переменных

Частной производной от функции по независимой переменнойх называют конечный предел ,вычисленный при постоянном у. Обозначается: или .

Частной производной от функции по независимой переменнойу называют конечный предел ,вычисленный при постоянном х. Обозначается: или .

Пусть функция z=f(x,y) имеет две непрерывные частные производные .

Произведение называетсячастным дифференциалом функции z=f(x,y) по х и обозначаются .

Произведение называетсячастным дифференциалом функции z=f(x,y) по х и обозначаются .

Полный дифференциал функции

Дифференциалом функции называется сумма произведений частных производных этой функции на приращение соответствующих независимых переменных, т. е. . Так как итогда можно записать: или .

Приложение полного дифференциала функции двух переменных к приближенным вычислениям

Так как при достаточно малых значениях иполное приращение функции приближенно равно ее дифференциалу, то, подставив в выражениевместоразность, получим:

данная формула используется для приближенных вычислений значений

Частные производные второго порядка

Пусть функция имеет частные производные первого порядка . Так как производные являются функциями аргументов х и у, то можно найти производные от этих функций. Частные производные этих функций называются частными производными второго порядка (вторыми частными производными) данной функции .

Так, для функции z = f(x, у) двух аргументов х и у (предполагается, что все производные первого порядка существуют) частные производные второго порядка:

.

Частные производные называются смешанными частными производными второго порядка.

Решение задач

Найти частные производные функций:

1. .

2..

Найти все частные производные второго порядка функции:

3. .

Найти частные и полный дифференциал для следующих функций:

4. .

5. .

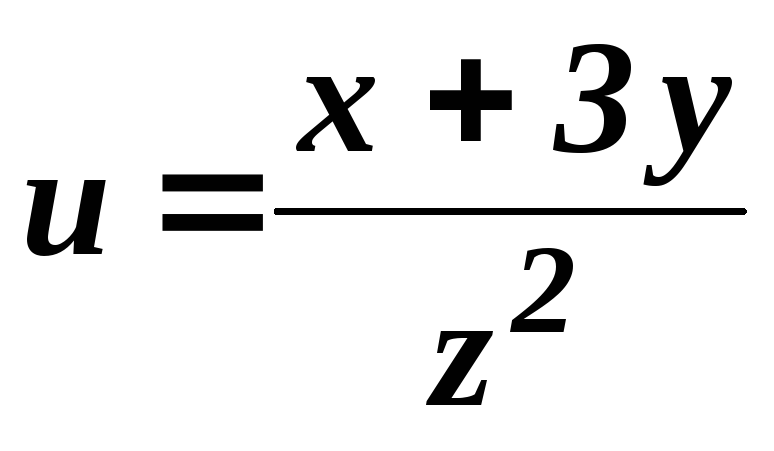6. Вычислить приближенно 1,03^5,05, исходя из значения функции прии заменяя ее приращение дифференциалом.